Para aumentar la precisión de flexión de los componentes de chapa metálica de los ascensores, se midió con precisión el radio de flexión (ángulo R) de materiales de uso común como SPC, SPHC, SUS304 y 804-GG en un ángulo de 90° utilizando una prensa plegadora CNC en chapa metálica. taller. Se utilizó un instrumento de medición óptico para determinar el radio de curvatura y el coeficiente de curvatura se calculó mediante calibres.
Los resultados de las pruebas sirven como referencia y brindan soporte de datos para la selección de herramientas de doblado apropiadas, aumentando la precisión del ángulo R durante el doblado y mejorando la precisión del cálculo de las dimensiones de doblado.
Importancia de la prueba
El radio de curvatura (dentro de R) y el coeficiente de curvatura son factores cruciales que afectan la calidad del proceso de curvatura. El radio de curvatura está asociado con la herramienta de curvatura, el espesor del material y los factores de rendimiento, mientras que el coeficiente de curvatura está determinado por el espesor del material, el radio de curvatura y el ángulo de curvatura. El coeficiente de flexión también afecta las dimensiones desplegadas de la pieza.
La fórmula actual para calcular el factor de flexión de 90° es α = 1,36t + 0,43R (donde t representa el espesor de la placa de material). Algunos de los errores comunes en el cálculo del factor de flexión incluyen:
- La diferencia entre el valor y el espesor real del material.
- La desviación entre la flexión real dentro de R y la flexión interna requerida como se indica en el dibujo (dentro de R generalmente se toma del dibujo al calcular α).
- El uso de la medición del calibre R (donde los valores del calibre R por debajo de R3 son 0,25 y por encima de R3 son 0,5) para determinar la flexión R, lo que da como resultado una menor precisión.
- No se tiene en cuenta la influencia del material y del método de flexión sobre la flexión R.
Cuando una pieza se dobla varias veces, el error en el coeficiente de flexión se acumula, lo que genera una precisión dimensional deficiente en el producto terminado.
Para resolver estos problemas, este experimento midió el espesor real de varios materiales de flexión, utilizó un instrumento de medición óptica para determinar con mayor precisión el radio de flexión interno y externo, calculó el coeficiente de curvatura real de la pieza y comparó los resultados con la fórmula. Esto ayudará a seleccionar matrices de doblado apropiadas, mejorará la precisión del doblado y conformado R y ampliará la precisión de los cálculos dimensionales.
Esquema de prueba
Material de exámen
Los materiales de prueba utilizados en el experimento fueron SPCC, SPHC, SUS304 y 804-GG, que fueron adquiridos por nuestra empresa. Las especificaciones de espesor para cada material se pueden encontrar en la Tabla 1.
Tabla 1 Materiales de prueba y espesor (mm)
|
Espesor toneladas/mm |
1.0 | 1.2 | 1.5 | 2.0 | 2.3 | 2.5 | 3.0 | 3.2 | 4.5 | 6.0 |
| SPCC | √ | √ | √ | √ | √ | √ | ||||
| SPHC | √ | √ | √ | |||||||
| SUS304 | √ | √ | √ | √ | √ | |||||
| 804-GG | √ |
muestra de prueba
El tamaño de las muestras utilizadas en el experimento fue de 100 mm x 100 mm y se produjeron mediante corte y corte por láser. Esto aseguró que la precisión dimensional de las muestras estuviera en el nivel de 0,1 mm.
Equipo de prueba
La máquina dobladora de prueba utilizada en el experimento fue una máquina dobladora CNC ubicada en el taller de producción de chapa de ascensor. La ranura en V utilizada en el experimento incluía FASTI-50 y Beyeler, y se seleccionó el troquel de cimitarra superior, como se ilustra en la Figura 1.
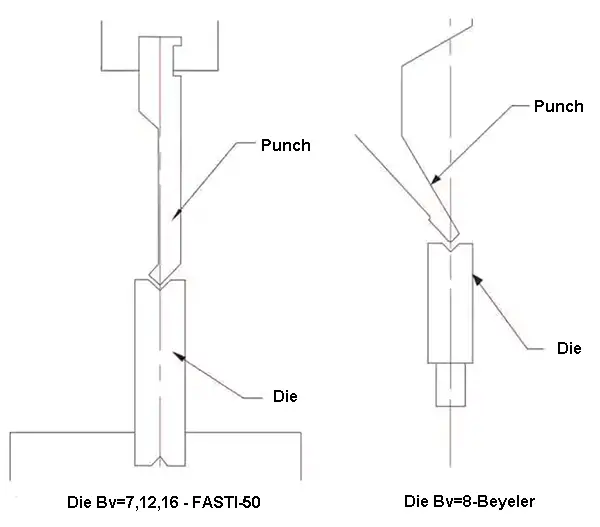
Fig.1 Matriz de doblado con ranura en V
La plegadora de tres puntos utilizada en el experimento fue una 3P250. El troquel superior del cuchillo recto seleccionado para el experimento incluía tanto el cortador puntiagudo R7 como el cortador redondo R9, como se ilustra en la Figura 2.
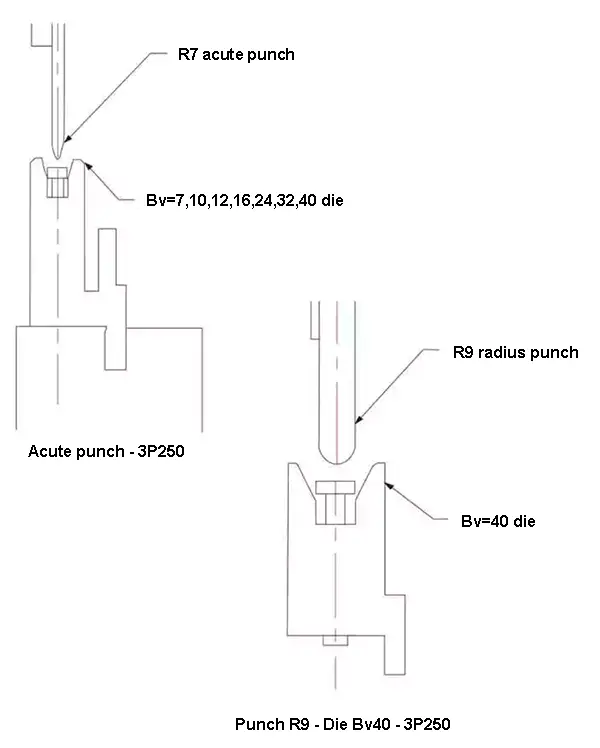
Fig.2 Matriz de flexión de tres puntos
Tabla 2 Los parámetros de la prensa plegadora, punzonadora y matriz.
| Apertura de matriz (Bv/mm) Prensa de freno y tipo punzón |
7 | 8 | 10 | 12 | dieciséis | 24 | 32 | 40 | |
|---|---|---|---|---|---|---|---|---|---|
| Apertura V (Golpe de cuello de cisne) |
Beyeler | √ | |||||||
| FASTI-50 | √ | √ | √ | ||||||
| Tres puntos (golpe directo) |
3P250 | √ | √ | √ | √ | √ | √ | √ | |
Método de prueba
El espesor real de las muestras se midió utilizando un micrómetro y se calculó el promedio de cuatro piezas para cada espesor específico. Las muestras se doblaron utilizando diferentes matrices de doblado en un ángulo de flexión de (90 ± 1)°, con el objetivo de garantizar que un lado de las muestras tuviera 50 mm de largo, como se ilustra en la Figura 3.
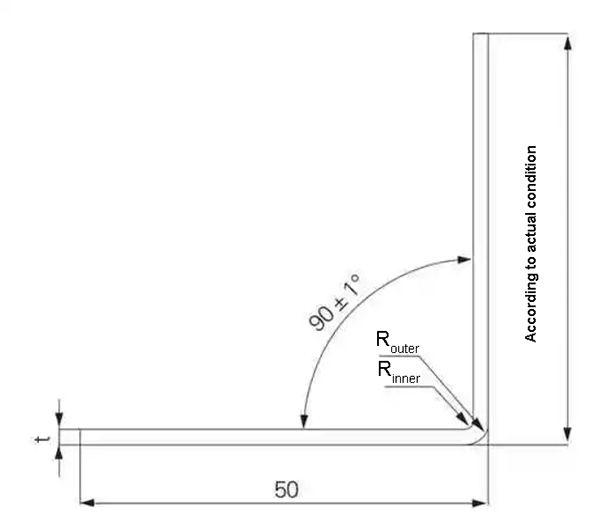
Figura 3 Diagrama de prueba de flexión
Cada especificación de espesor se repitió 5 veces durante el proceso de doblado. Una vez finalizada la flexión, se escanearon los contornos del ángulo de flexión utilizando un instrumento de medición óptico para calcular el ángulo de flexión externo (R externo) y el ángulo de flexión interno (R interno), como se ilustra en la Figura 4.
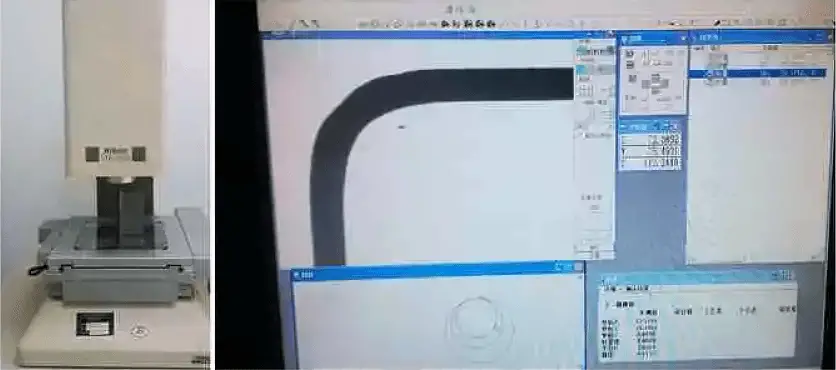
Fig. 4 Instrumento de medición óptico y medición del ángulo de flexión R
Se utilizó un calibre para medir la longitud de ambos lados para calcular el coeficiente de flexión. Cada especificación de espesor se repitió 5 veces y se obtuvo el valor promedio.
Resultados y análisis de las pruebas.
La tabla adjunta es una recopilación de los resultados de las pruebas. Los datos que se muestran en la tabla incluyen el espesor real del material de prueba, el radio de curvatura interior y exterior de 90°, el coeficiente de curvatura y el adelgazamiento de la curvatura.
Espesor real del material
La Tabla 3 compara el espesor real de la muestra, medido con un micrómetro, con su espesor nominal.
Tabla 3 El espesor real de los materiales de prueba (mm)
| Espesor nominal | 1.0 | 1.2 | 1.5 | 2.0 | 2.3 | 2.5 | 3.0 | 3.2 | 4.5 | 6.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Espesor real | SPCC | 1.00 | 1.18 | 1,48 | 2.01 | 2.50 | 2,97 | ||||
| SPHC | 3.13 | 4:20 am | 5.91 | ||||||||
| SUS304 (Retire la película) |
0,93 | ||||||||||
| 804-GG | 2.26 | ||||||||||
La tabla revela que la diferencia entre el espesor real de SPCC y su espesor nominal está dentro de 0,03 mm. Se encontró que el espesor real del material SUS304 sin recubrimiento era aproximadamente 0,07 mm más delgado que su espesor nominal. Se midió que el espesor real de la lámina laminada en caliente SPHC de 4,5 mm era de 4,2 mm.
Duplicar el ángulo interno R interno
Al comparar la R interna bajo diferentes condiciones de flexión, se puede ver que la R interna está influenciada por el material, el espesor de la placa, el método de flexión y las herramientas de flexión.
De estos cuatro factores, la situación de otros tres es la misma:
- R interno (SUS304) > R interno (SPCC).
Si el ancho de la ranura en VB v = 12 mm, la R interna en SPCC con espesor de 1,2 mm y SUS304 es de 1,85 mm y 2,09 mm, respectivamente.
- Cuando la matriz de doblado es la misma, para el mismo material, el espesor interno de la placa de influencia R es menor.
Por ejemplo, cuando B v = 12 mm en flexión de tres puntos, la R interna en el espesor de 1,0 ~ 2,0 mm de SUS304 es 2,33 ~ 2,51 mm, la diferencia no es significativa.
- R interior (tres puntos) > R interior (ranura en V).
La comparación del mismo ancho de ranura doblando el troquel inferior (B v = 7 mm, 12 mm y 16 mm) muestra que la flexión interna R en tres puntos es ligeramente mayor que la de la ranura V.
- Cuanto mayor sea el ancho de la ranura B v, mayor será la R interna y mayor la R interna correspondiente
La Figura 5 es una comparación de los ángulos de flexión de tres puntos R para la ranura de matriz inferior cuyo ancho Bv es de 24 mm, 32 mm y 40 mm, correspondientes a aproximadamente 4,0 mm, 4,7 mm y 5,9 mm de R interno respectivamente.

Fig. 5 Comparación del radio interior del codo SPHC de 4,5 mm con diferentes anchos de canal (punzón puntiagudo de tres puntas)
Por lo tanto, además del ancho de la ranura de la matriz de doblado B v del material, el método de doblado (ranura en V y tres puntos) también afecta la flexión interna R a la que debemos prestar atención.
Relación de reducción y ángulo de flexión exterior R exterior
En la prueba, la diferencia entre R exterior y R interior se utiliza para representar el espesor promedio cerca del ángulo de flexión, es decir, t' = R exterior –R interior .
Por tanto, la relación de reducción es η = (t – t')/t.
A partir de los datos de la tabla adjunta, se puede ver que la reducción de espesor se produjo en todos los casos de este caso de prueba.
La mayor parte de la tasa de reducción está en el rango del 6% al 15%, y la influencia del espesor del material, el modo de flexión y el ancho de la ranura en la tasa de adelgazamiento es más complicada y la regla es difícil de identificar.
Sin embargo, está claro que la tasa de dilución de SPHC es menor, alrededor del 4% al 6%.
O de la prueba interna utiliza un instrumento de medición óptico para calcular el barrido, mientras que se puede calcular el valor de redondez.
(1) Cuando Bv = 7 ~ 16 mm, el valor de redondez de R interior y R exterior es muy pequeño, en su mayoría ≤ 0,05 mm, lo que indica que los contornos de las esquinas interior y exterior dobladas coinciden perfectamente con el grado de redondez.
(2) Cuando Bv = 24 mm, 32 mm y 40 mm (todos del tipo de tres puntos), los valores de redondez de R interior y R exterior aumentan ligeramente, superando 0,1 mm, lo que significa que después del ancho de ranura Bv del doblado inferior los troqueles aumentan a 24 mm, el grado de arco de los contornos interior y exterior del doblez disminuye.
Coeficiente de flexión α
El cronograma también proporciona los valores medidos y calculados de la prueba del coeficiente de flexión (método utilizado actualmente para calcular el coeficiente de flexión, fórmula de cálculo: α = 1,36t + 0,43R interno ).
A modo de comparación, la diferencia no es grande (en el cálculo, el espesor interno t y R se incluyen en el cálculo mediante el valor de prueba real), lo que indica que la fórmula actual del coeficiente de flexión α = 1,36t + 0,43R interno es Universal, el coeficiente de flexión depende de dos parámetros: el espesor real t del material y la flexión real R interna .
El R interno está influenciado por el material, el espesor de la placa, el método de doblado y la herramienta de doblado; el R interno real es el método más simple y efectivo.
Para materiales nuevos o piezas dobladas con otros espesores, es necesario medir el espesor real y la flexión interna R de la herramienta de flexión.
Conclusión
Del análisis anterior se pueden obtener varias conclusiones:
(1) Los resultados de las pruebas muestran los coeficientes de flexión R interior R exterior y de flexión de varias láminas gruesas de uso común de SPCC, SPHC, SUS304, 804-GG en talleres de chapa, máquinas dobladoras CNC como Beyeler, FASTI-50 y 3P250;
(2) La R interna no solo está relacionada con la matriz de doblado, sino también con el material;
La prueba muestra que el R interno de SUS304 es ligeramente mayor que el de SPCC bajo los mismos parámetros de flexión;
(3) Cuando los otros parámetros de flexión son iguales, el R interno de la flexión de tres puntos es ligeramente mayor que el de la ranura en V, por lo que se debe considerar el centro de trabajo de flexión al seleccionar el coeficiente de flexión;
(4) La fórmula para calcular el coeficiente de flexión interna α=1,36t+0,43R es universal.
La acumulación del espesor real de los materiales de flexión comúnmente utilizados en el taller y el correspondiente molde de flexión que forma la R interna puede calcular un coeficiente de flexión más preciso.

























































