Ha habido avances notables en ingeniería a lo largo de los años y un método que ha desempeñado un papel crucial en la resolución de problemas complejos es el método de elementos finitos (MEF). Esta poderosa técnica numérica ha revolucionado el análisis de ingeniería, permitiendo a ingenieros y científicos simular y analizar el comportamiento de sistemas complejos. En este artículo, profundizaremos en las complejidades del método de elementos finitos, sus aplicaciones, ventajas y desafíos, y exploraremos sus perspectivas futuras.
El método de los elementos finitos es una técnica matemática utilizada para aproximar soluciones de ecuaciones diferenciales que describen diversos fenómenos físicos. Fue desarrollado originalmente en la década de 1940 y desde entonces se ha convertido en un enfoque ampliamente utilizado para resolver problemas complejos de ingeniería. Al dividir un sistema continuo en elementos más pequeños e interconectados, FEM permite un análisis numérico eficiente.
Historia del método de los elementos finitos.
El Método de Elementos Finitos (FEM) es una técnica numérica para resolver problemas complejos de ingeniería y matemáticas. Se utiliza en muchas áreas, incluido el análisis estructural, la dinámica de fluidos, la transferencia de calor y el electromagnetismo. El desarrollo del FEM tiene una rica historia que abarca varias décadas. Aquí un breve resumen de su desarrollo:
- Inicios: Los orígenes del método de elementos finitos se remontan a principios de la década de 1940. Los ingenieros aeronáuticos buscaban métodos para resolver los problemas de análisis estructural encontrados en la construcción de aeronaves. JH Argyris, un ingeniero griego, desarrolló un método llamado "método Rayleigh-Ritz" en 1942, que sentó las bases para el análisis de elementos finitos.
- Análisis de estructura matricial: En las décadas de 1950 y 1960 surgió el campo del análisis estructural matricial, liderado por pioneros como Richard Courant, Ray W. Clough y Olgierd Zienkiewicz. Aplicaron técnicas de álgebra matricial para resolver problemas estructurales, allanando el camino para el desarrollo del análisis de elementos finitos.
- Desarrollo del método de los elementos finitos: Olgierd Zienkiewicz, conocido como el "padre del método de los elementos finitos", jugó un papel crucial en su desarrollo. A finales de la década de 1950, Zienkiewicz trabajó con Michael Turner para formular el concepto de dividir estructuras complejas en elementos más pequeños y manejables. Combinaron este enfoque con métodos matriciales, lo que dio como resultado la primera formulación FEM verdadera en 1960.
- Avances y expansión: Se lograron avances significativos en FEM en las décadas de 1960 y 1970. Los esfuerzos de investigación se centraron en refinar formulaciones matemáticas, mejorar las formas y tipos de elementos y desarrollar algoritmos numéricos eficientes. El desarrollo de software comercial de elementos finitos, como NASTRAN (Sistema de Análisis Estructural de la NASA), ha ampliado el uso de FEM en múltiples industrias.
- Aplicación en expansión: En las décadas de 1980 y 1990, FEM se expandió más allá del análisis estructural a otras áreas, incluida la transferencia de calor, la dinámica de fluidos y el electromagnetismo. Los investigadores han desarrollado formulaciones específicas de elementos finitos para satisfacer las necesidades únicas de estas áreas.
- Desarrollos en curso: El método de elementos finitos ha evolucionado desde la década de 2000. Los avances en la potencia informática y los algoritmos numéricos han permitido simulaciones más precisas y han aumentado la complejidad de los problemas que pueden resolverse. Además, nuevas técnicas como el refinamiento adaptativo de la malla y la cuantificación de la incertidumbre han mejorado la confiabilidad y eficiencia de las simulaciones FEM.
Hoy en día, el método de los elementos finitos es una herramienta indispensable en la ingeniería y la investigación científica. Su rica historia y continuos desarrollos los han convertido en una técnica numérica fundamental para resolver una amplia gama de problemas complejos, contribuyendo así al avance de numerosas áreas de investigación.
Comprender los conceptos básicos del método de los elementos finitos.
FEM incluye una serie de pasos para analizar un sistema.
Primero, se establece la formulación matemática del problema, definiendo las leyes físicas y las ecuaciones subyacentes.
Luego, el sistema continuo se discretiza en elementos más pequeños para que la solución pueda aproximarse dentro de cada elemento. Este proceso de discretización forma la base para cálculos posteriores.
La generación de mallas es un paso crítico en el método de elementos finitos. El área se divide en elementos más pequeños, como triángulos o cuadriláteros para problemas 2D, o tetraedros o hexaedros para problemas 3D.
La calidad de la red afecta la precisión de los resultados. Por lo tanto, se tiene cuidado de garantizar que se utilice una red adecuada para el problema en cuestión.
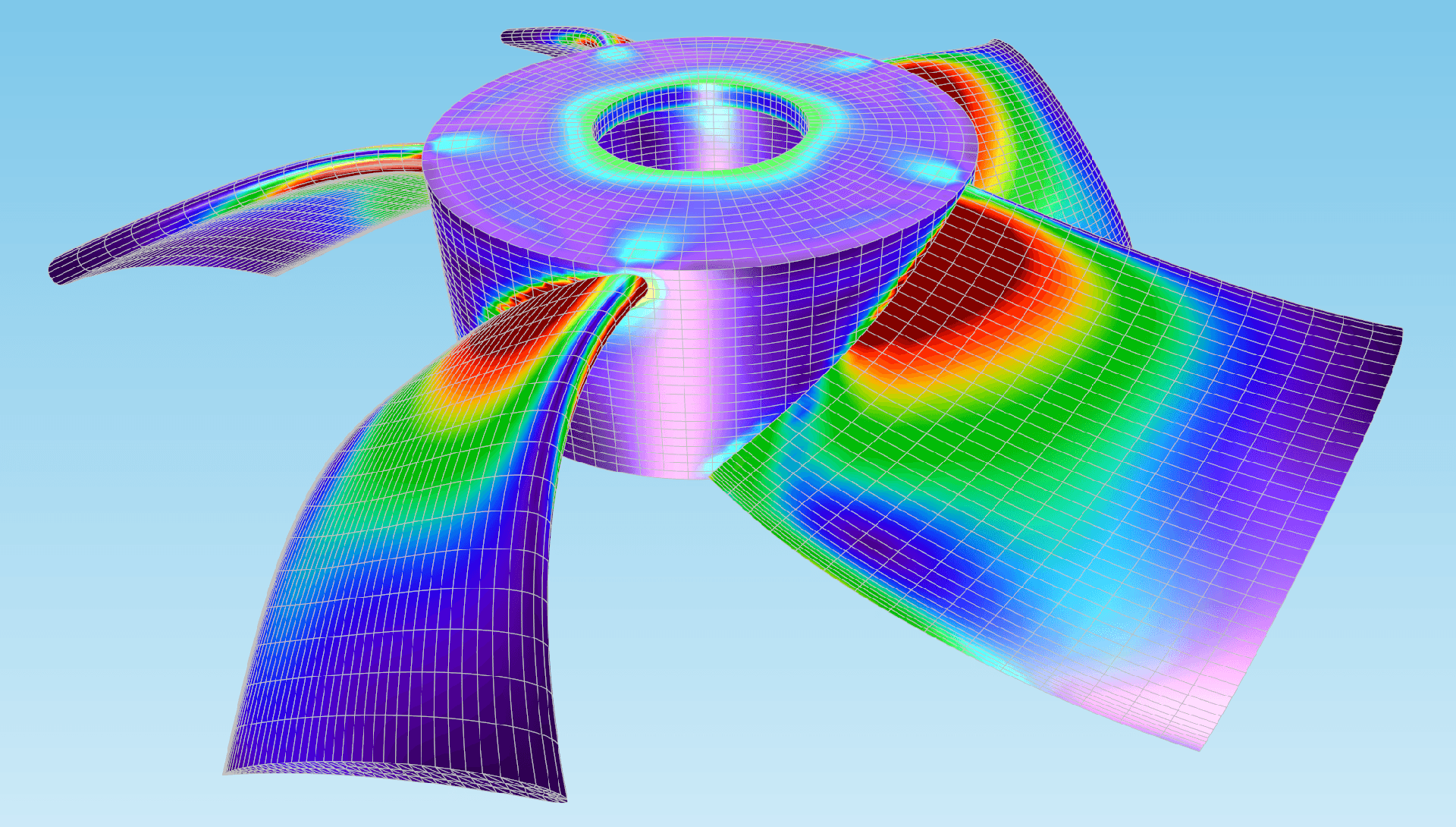
Aplicaciones del método de los elementos finitos
El método de elementos finitos (MEF) tiene una amplia gama de aplicaciones en diferentes áreas. Es una técnica numérica versátil que se puede utilizar para resolver problemas complejos en ingeniería, física y matemáticas. Estas son algunas de las principales aplicaciones del método de los elementos finitos:
- Análisis estructural : FEM se utiliza ampliamente en ingeniería civil para estudiar el comportamiento de estructuras bajo diferentes condiciones de carga . Puede predecir con precisión tensiones, deformaciones, desplazamientos y fallas de varios tipos de estructuras, como edificios, puentes, aviones y componentes de automóviles.
- Dinámica de fluidos : FEM se utiliza en dinámica de fluidos computacional (CFD) para estudiar el comportamiento del flujo de fluidos, incluida la aerodinámica, la hidrodinámica y la transferencia de calor. Permite la simulación de sistemas de fluidos complejos, como por ejemplo: el flujo de aire sobre el ala de un avión, el flujo de agua en tuberías y el comportamiento de los líquidos en procesos industriales.
- Transferencia de calor y termodinámica : FEM se utiliza para analizar la conducción, convección y radiación del calor en sistemas térmicos. Permite la predicción de distribuciones de temperatura, tasas de transferencia de calor y el desarrollo de sistemas de refrigeración eficientes.
- Electromagnetismo : FEM se aplica en el análisis de campos y dispositivos electromagnéticos. Puede modelar y simular fenómenos electromagnéticos, incluida la propagación de ondas electromagnéticas, el diseño de antenas, el análisis de campos magnéticos y el comportamiento de máquinas eléctricas.
- Geotecnia : FEM se utiliza para analizar la interacción suelo-estructura y problemas geotécnicos. Ayuda a evaluar la estabilidad de cimientos, taludes, túneles y estructuras subterráneas. FEM también es útil para analizar el comportamiento de presas, muros de contención y consolidación de suelos.
- Biomecánica e ingeniería biomédica : FEM juega un papel crucial en el modelado y simulación del comportamiento mecánico de estructuras y tejidos biológicos. Ayuda a estudiar la mecánica de huesos, articulaciones, tejidos blandos e implantes. FEM se utiliza para optimizar el diseño de dispositivos médicos como prótesis e implantes ortopédicos.
- Industrias automovilística y aeronáutica : FEM se utiliza ampliamente en las industrias automovilística y aeroespacial para análisis estructurales, simulación de accidentes, análisis de vibraciones y optimización del diseño de componentes. Ayuda a mejorar el rendimiento, la seguridad y la eficiencia de vehículos y aeronaves.
- Tecnología y materiales de fabricación : FEM se utiliza en la simulación de procesos como el formado, la soldadura y la fundición de metales. Ayuda a predecir tensiones y deformaciones residuales y a optimizar los procesos de fabricación. FEM también se utiliza para estudiar el comportamiento de materiales, como las propiedades mecánicas de metales, compuestos y polímeros.
Estos son sólo algunos ejemplos de la amplia gama de aplicaciones del método de los elementos finitos. Su capacidad para resolver problemas complejos y proporcionar información detallada sobre el comportamiento de los sistemas los convierte en una herramienta indispensable en la ingeniería y la investigación científica.
Ventajas y desventajas del método de los elementos finitos.
El método de elementos finitos ofrece varias ventajas que contribuyen a su amplio uso.
En primer lugar, proporciona un marco flexible que puede manejar geometrías y propiedades de materiales complejas. Esta flexibilidad permite un modelado preciso de estructuras y sistemas reales. Además, el método es adaptable a diferentes tipos de problemas, incluidos análisis lineales y no lineales, simulaciones transitorias o dinámicas y problemas multifísicos acoplados.
Además, el método de los elementos finitos ofrece un enfoque sistemático para la resolución de problemas. Divide un problema complejo en elementos más pequeños y manejables, lo que permite a los ingenieros centrarse en el comportamiento local y luego sintetizar los resultados en una solución global. Este enfoque modular mejora la potencia computacional y permite el procesamiento paralelo, lo que reduce el tiempo necesario para el análisis.
A pesar de sus numerosas ventajas, el método de los elementos finitos tiene algunas limitaciones. Una gran desventaja es la posibilidad de errores debido a cálculos aproximados. La precisión de los resultados depende de factores como la calidad de la malla, el tamaño del elemento y la elección de los métodos numéricos. En algunos casos, pueden ser necesarias técnicas especiales, como el refinamiento adaptativo de la malla, para mejorar la precisión.
Avances recientes en el método de los elementos finitos
Con los avances tecnológicos, FEM ha ido evolucionando e incorporando nuevos desarrollos. Una tendencia notable es la integración de inteligencia artificial (IA) y técnicas de aprendizaje automático en el proceso de análisis de elementos finitos. La IA puede mejorar la precisión de las simulaciones, automatizar el proceso de mallado y optimizar los diseños aprovechando grandes cantidades de datos. Esta integración tiene el potencial de revolucionar el análisis de ingeniería y permitir simulaciones más eficientes y precisas.
Perspectivas de futuro y posibles desafíos
El futuro del método de los elementos finitos parece prometedor. La investigación y el desarrollo continuos tienen como objetivo afrontar los desafíos actuales y ampliar sus capacidades. Los avances en potencia informática, algoritmos numéricos y computación paralela mejorarán aún más la eficiencia y precisión de las simulaciones.
Sin embargo, también es necesario superar algunos desafíos. La creciente complejidad de los problemas de ingeniería requiere modelos matemáticos más sofisticados, que pueden requerir importantes recursos computacionales. Además, la validación y verificación de los modelos de elementos finitos sigue siendo esencial para garantizar resultados precisos y fiables.
El método de los elementos finitos revolucionó el análisis de ingeniería al proporcionar una poderosa técnica numérica para resolver problemas complejos. Sus aplicaciones abarcan diversas áreas, incluido el análisis estructural, la dinámica de fluidos y el análisis de transferencia de calor. Con avances continuos, como la integración de la IA y el aprendizaje automático, se espera que el método de elementos finitos desempeñe un papel aún más importante en las simulaciones de ingeniería y la optimización del diseño.
Preguntas frecuentes
1. ¿Cuáles son las principales ventajas de utilizar el método de los elementos finitos?
FEM ofrece varias ventajas, incluida su capacidad para manejar geometrías y propiedades de materiales complejas, su adaptabilidad a diferentes tipos de problemas y su enfoque modular que mejora el rendimiento computacional.
2. ¿Se puede aplicar el método de los elementos finitos a problemas no lineales?
Sí, FEM puede manejar problemas no lineales incorporando modelos de materiales apropiados y técnicas numéricas para resolver las ecuaciones rectoras.
3. ¿En qué se diferencia el método de los elementos finitos de otros métodos numéricos?
FEM discretiza el área en elementos más pequeños, mientras que otros métodos, como los métodos de diferencia o volumen, dividen el área en una cuadrícula o volumen de control. La elección del método depende del problema en cuestión y de los requisitos específicos del análisis.
4. ¿Qué software se utiliza habitualmente para el análisis de elementos finitos?
Existen varios paquetes de software populares para el análisis de elementos finitos, incluidos ANSYS, Abaqus, COMSOL Multiphysics y LS-DYNA. Estas herramientas de software ofrecen una interfaz fácil de usar y una amplia gama de funciones para realizar simulaciones y analizar resultados.
5. ¿Existen limitaciones en el tamaño de los problemas que se pueden resolver utilizando el método de elementos finitos?
El tamaño del problema que se puede resolver utilizando el método de elementos finitos depende de factores como los recursos computacionales, la memoria y la complejidad del problema. Los grandes problemas con millones de grados de libertad pueden requerir computación de alto rendimiento o técnicas de procesamiento paralelo para producir resultados en un tiempo razonable.

