El pandeo lateral por torsión es la deformación de la viga con respecto a su eje longitudinal debido a las cargas aplicadas. Además, provoca fallos en las vigas de acero.
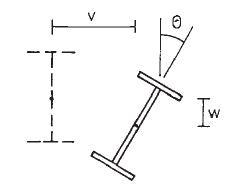
La deformación puede ocurrir como movimiento de traslación y rotación de la sección. Este tipo de movimientos se denominan pandeo flexo-torsional. La Figura 1 muestra las deformaciones que pueden ocurrir como resultado del pandeo por flexión-torsión.


Figura 01 Doblar y torcer
Como se muestra en la Figura 01, la viga se puede decodificar aplicando cargas. Esta deformación puede ocurrir cuando el componente se gira lateral y verticalmente. Al diseñar vigas de acero, se proporcionan soportes laterales a intervalos calculados para evitar fallas.
El pandeo lateral por torsión ocurre con cargas crecientes basadas en las propiedades de la sección transversal y sus limitaciones. Las cargas sobre una viga no se pueden evitar porque ese es el propósito de la viga.
Sin embargo, las propiedades de la sección transversal y las condiciones de restricción se pueden controlar durante la fase de construcción y diseño.
- Como se explicó anteriormente, el pandeo por flexión y torsión ocurre cuando la viga no está completamente restringida en la dirección lateral a lo largo del ala comprimida de la viga.
- La viga se considera totalmente fija lateralmente si la conexión entre la viga y el piso puede soportar al menos una fuerza lateral del 2,5% de la fuerza máxima en el ala comprimida de la viga.
Si no hay restricciones, se deberán proporcionar tramos con un módulo de sección superior. Si las restricciones se proporcionan adecuadamente, se puede reducir el tamaño del transportador.
Se ha demostrado que durante las fallas el momento de la sección se aleja de su eje. Por lo tanto, al proporcionar límites, las dimensiones de la sección definitivamente se reducirán.
Sin embargo, debido a la disposición estructural de la estructura, puede que no sea posible proporcionar límites laterales en los extremos o en el interior. En estas situaciones, las vigas deben diseñarse sin considerar limitaciones laterales.
Principalmente, la falta de fijación de la brida de presión provoca un movimiento lateral del perfil. Por lo tanto, el pandeo por torsión se puede evitar mediante el frenado interno.
Se proporcionan soportes intermedios para reducir la longitud sin soporte en la dirección lateral. Deben soportar fuerzas laterales y tener la capacidad de mantenerlas sin deformarse. La capacidad de carga axial de los soportes intermedios debe comprobarse de acuerdo con la guía BS 5950.
Diseño de pandeo por flexión-torsión de una viga.
Para cumplir con los requisitos de flexión, la sección debe tener una capacidad de flexión en la dirección de flexión (Mc) mayor que el momento flector aplicado y una capacidad de pandeo por torsión lateral mayor que el momento generado por el pandeo.
M X < M b /M LT y M X ≤M C
En este artículo se explica el procedimiento a seguir para calcular la capacidad de pandeo lateral por torsión. Y es posible que se requiera el artículo Construcción de vigas de acero según BS 5950, pruebas de capacidad de flexión.
La resistencia al pandeo por torsión en flexión (M b /M LT ) se puede calcular como se muestra a continuación. Dos métodos para calcular el momento resistente de pandeo (M b ). Se puede utilizar cualquiera de los métodos según las preferencias del diseñador.
- Método riguroso
- Método simplificado
| Método riguroso | Método simplificado | |
| Clase 1 – Plástico Clase 2 – Compacto |
Mb = PbSX | Mb = PbSX |
| Clase 3 – Semicompacto | M segundo =P segundo Z X o M b =P b S x,efe |
Mb = PbZX |
| Clase 4 – Delgado | M b =P b Z x,efe | |
| P b basado en λ LT y P j | P b basado en √(β i ) I E /R j y relación D/T | |
| λ LT = uvλ √( β i ) |
Al comparar los dos métodos, la principal diferencia parece ser el método utilizado para evaluar la resistencia a la flexión (P b ).
Para una explicación detallada del método de construcción de vigas de acero, consulte el artículo Ejemplo práctico de construcción de una viga de acero .
Detectar pandeo por flexión y torsión
Ejemplo de pandeo torsional
Datos:
- Considere una viga simplemente apoyada sin restricciones intermedias.
- Extensión de soporte 6m
- Momento flector máximo de diseño 100 kNm
Como se explicó anteriormente, existen dos métodos para detectar el pandeo por flexión y torsión. Expliquemos esto con un ejemplo práctico.
Para que una sección sea resistente a la flexión, debe satisfacer la siguiente ecuación.
M X < M b /M LT
Por simplicidad, en este ejemplo no se consideran restricciones intermedias.
Entonces,
MLT = 0,925, Tabla 18, BS 5950
M b =P b S X Sección 4.3.6.4
Primero, verifiquemos la resistencia al pandeo con un método riguroso.
En el cálculo se tienen en cuenta los siguientes datos de ruta
- T = 500 mm
- T = 16 mm
- t = 10 mm
- B = 200 mm
- b = 100 mm
- R1 = 20 mm
- d = 500 – 16 x 2 – 2 x 20 = 428 mm
- SX = 2175 × 10 3 mm 3
- Z X = 1914 × 10 3 mm 3
- R j = 43,3 mm
- El perfil está fabricado en plástico según sus dimensiones.
Método riguroso
Mb = PbSX
P b es función de λ LT y P j
λLT =uvλ√( βi )
λ = I E /R j
M E – se puede obtener de la Tabla 13 (Sección 4.3.5.1) y tiene en cuenta L LT = L – span
Por lo tanto,
M E = 1,0 L LT = 1 x 6 = 6 metros
λ = I E /R j = 6.000/43,3 = 138,568
La sección 4.3.6.8 se aplica a los perfiles laminados I y H.
x = D / T usado con u = 0,9
x = D/T = 500/16 = 31,25
β i se puede encontrar en la Sección 4.3.6.9
β i = 1 para perfiles plásticos clase 1 o perfiles compactos clase 2
v – factor de esbeltez – se deriva de la Tabla 19 según λ / x y η
λ/x = 138,568/31,25 = 4,434
Para bridas del mismo tamaño η = 0,5
v = 0,84 de la Tabla 19 ( se supone un valor conservador; λ/x = 4,5, se debe utilizar la interpolación para el valor exacto )
λ LT =uvλ√(β i ) = 0,9 x 0,84 x 138,568 x √(1) = 104,8
λ ELA se puede encontrar en la Tabla 16 (indicado a continuación en la Tabla 16)
Si λ ELA ≥λ LT ; P b =P j o bien P b se puede encontrar en la Tabla 16 para perfiles laminados.
Si λ ELA ≥λ LT No es necesario tener en cuenta el pandeo por torsión; en caso contrario se deberá realizar una verificación de pandeo por torsión.
Pj = 275 N/ mm2 ; λELA = 34,3
λ ELLA <λ LT
Por lo tanto, verifique si hay pandeo por torsión.
Del Cuadro 16 para λ LT = 104,8; P b = 117 N/mm 2
M b = P b S X = 117 x 2175 x 10 3 x 10 -6 = 254,5 kN · m
Mb / MLT = 254,8 / 0,925 = 275,4 kNm
Por lo tanto, MX = 100kNm
La sección transversal es adecuada para pandeo lateral por torsión según el método estricto.
Método simplificado
No necesitamos hacer ambos cálculos para comprobar la resistencia al pandeo.
M b =P b S X : Párrafo 4.3.7
El propósito de P b no es el mismo que el del método riguroso.
Este método proporciona respuestas conservadoras.
P b se puede obtener de la Tabla 20 de BS 5950 según √(β i ) (EU E /R j ) y D/T
βi = 1; Igual que el cálculo anterior.
ME / Rj = 138,568; de los cálculos anteriores
√(β i ) (IE E /R j ) = 1 0,5 x 135,568 = 138,568
D/T = 500/16 = 31,25
Ahora puedes obtener de la tabla 20.
Pb = 116,646 N/ mm2
M segundo = P segundo S
Mb / MLT = 253,705 / 0,925 = 274,3 kNm
Entonces M es X = 100kNm
Por tanto, la sección es suficiente.