El ejemplo de diseño de una viga de acero trabajada explica la construcción de una viga simplemente apoyada con una carga uniformemente distribuida. La viga se considera simplemente apoyada y los datos de diseño para calcular el momento flector y las fuerzas cortantes se proporcionan a continuación.
Además, las propiedades de la sección transversal a considerar se especifican en los distintos pasos del ensayo.
Los aspectos teóricos y los procedimientos de diseño del código se analizan en el artículo Diseño de vigas de acero conforme a BS 5950 .
Datos de diseño
- Carga UDL 20 kN/m
- Extensión de viga 6m
- La viga está simplemente apoyada
- Resistencia de diseño del acero, Py = 275 N/mm 2
Momento flector máximo
= wl 2/8 = 20 x 6 2/8 = 90 kN·m
Fuerza de corte máxima
= wl/2 = 20 x 6/2 = 60 kN
Considere transportador universal 500x200x89,7 kg/m (P j = 275 N/mm 2 )
Datos de la sección
- T = 500 mm
- T = 16 mm
- t = 10 mm
- B = 200 mm
- b = 100 mm
- R1 = 20 mm
- d = 500 – 16 x 2 – 2 x 20 = 428 mm
- SX = 2175 × 10 3 mm 3
- Z X = 1914 × 10 3 mm 3
- R j = 43,3 mm
Comencemos a calcular el diseño de la viga de acero. Como parte de este cálculo de diseño de vigas de acero, se llevan a cabo las siguientes pruebas.
- Clasificación de secciones
- Diseño de corte
- Construcción curvada
- Verificar pandeo por torsión
- Control de deflexión
- Prueba de rodamiento de puente
- Prueba de pandeo web
Clasificación de secciones
El primer paso en el diseño de una viga de acero es clasificar la sección transversal para determinar si es plástica, semiplástica, compacta o esbelta.
T = 16 mm, P j = 275 N/mm 2
ε = (275/P j ) 0,5 = 1
Comprobar la brida
b/T = 100/16 = 6,25 < 9ε = 9 – La brida está hecha de plástico
consultar la web
d/t = 428/10 = 42,8 < 80ε = 80 – La red es de plástico
Además, d/t < 70ε = 70; por lo tanto, no se requiere verificación de pandeo por cortante.
Por tanto, la sección es plástica.
Diseño para fuerzas cortantes.
Fuerza cortante de diseño, F contra = 60 kN
P contra = 0,6p j A contra = 0,6p j tD = 0,6 x 275 x 10 x 500 x 10 -3 = 825 kN
f en contra
contra la capacidad de corte está bien
Dependiendo de la fuerza cortante, la construcción de la viga de acero decide si la sección transversal estará expuesta a una fuerza cortante baja o alta.
Construcción flexible
Compruebe si la sección está sujeta a corte alto o bajo.
60% XP contra = 0,6 x 825 = 495 kN
F vs <0.6P vs Sección de bajo corte
M C debe ser inferior a 1,2P j Z X o P j S X de acuerdo con la Sección 4.2.5.1 y la Sección 4.2.5.2
M C ≤1,2P j Z X = 1,2x275x1914x10 3 x 10 -6 = 613,62 kN·m
M C = P j S
Por lo tanto,
CM = 598,125 kNm > 90 kNm
Bien plegable
Detectar pandeo por flexión y torsión
M X < M b /M LT
En este ejemplo no se consideraron restricciones intermedias.
MLT = 0,925, Tabla 18, BS 5950
M b =P b S X Sección 4.3.6.4
Existen dos métodos para comprobar el pandeo lateral por torsión, como se describe en el artículo Construcción de vigas de acero según BS 5950 . Estos son el método estricto y el método simplificado.
En este ejemplo de diseño de vigas de acero, analizamos ambos métodos para explicar con más detalle los procedimientos que deben seguirse en ambos métodos.
Más allá y más allá La principal diferencia entre estos dos métodos es la evaluación de la resistencia a la flexión .
Método riguroso
Mb = PbSX
P b depende de λ LT y P j
λLT =uvλ√( βi )
λ = I E /R j
M E – tomado de la Tabla 13 de acuerdo con la Sección 4.3.5.1 y teniendo en cuenta L LT = L – span
M E = 1,0 L LT = 1 x 6 = 6 metros
λ = I E /R j = 6.000/43,3 = 138,568
La sección 4.3.6.8 se aplica a los perfiles laminados I y H.
x = D / T usado con u = 0,9
x = D / T = 500/10 = 50
β i se puede encontrar en la sección 4.3.6.9
β i = 1 para perfiles plásticos clase 1 o perfiles compactos clase 2
v – factor de esbeltez, que se determina en la Tabla 19 con base en λ / x y η
λ/x = 138,568/50 = 2,771
η = 0,5 para bridas isósceles
v = 0,919 de la Tabla 19
λ LT =uvλ√(β i ) = 0,9 x 0,919 x 138,568 x √(1) = 114,6
λ ELA se puede encontrar en la Tabla 16 (ver tabla a continuación)
Si λ ELA ≥λ LT ; P b =P j o bien P b se puede encontrar en la Tabla 16 para perfiles laminados.
Si λ ELA ≥λ LT No es necesario tener en cuenta el pandeo por torsión; en caso contrario se deberá realizar una verificación de pandeo por torsión.
Pj = 275 N/ mm2 ; λELA = 37,3
λ ELA <λ LT Por lo tanto, verifique si hay pandeo por torsión.
De la Tabla 16 para λ LT = 114,6; P b = 102 N/mm 2
M b = P b S X = 102 x 2175 x 10 3 x 10 -6 = 221,85 kN · m
Mb / MLT = 221,85 / 0,925 = 239,838 kNm
Por lo tanto, MX = 90kNm
La sección es suficiente .
Método simplificado
Nota: No es necesario utilizar ambos métodos al dimensionar una viga. Simplemente siga el método simplificado o estricto.
M b =P b S X : Párrafo 4.3.7
Con este método la determinación de P b es diferente al método anterior. Este método proporciona respuestas conservadoras. P b se puede encontrar en la Tabla 20 de BS 5950 basado en √(β i ) ( IE /R j ) y D/T
βi = 1; calculo previo
ME / Rj = 138,568; calculo previo
√(β i ) (IE E /R j ) = 1 0,5 x 135,568 = 138,568
D/T = 500/16 = 31,25
P b = 116,646 N/mm 2 De la tabla 20
M segundo = P segundo S
Mb / MLT = 253,705 / 0,925 = 274,3 kNm
Por lo tanto, MX = 90kNm
la sección es suficiente
Desvío
La deflexión máxima (δ) para una viga simplemente apoyada con distribución uniforme se puede calcular utilizando la siguiente ecuación.
δ = 5W t M 4 / (384EI)
Esta ecuación se puede simplificar aún más de la siguiente manera.
δ = 0,104 M Máx. M 2 / (EI)
Mientras evaluamos la deflexión en función de las cargas aplicadas, asumimos una carga aplicada de 10 kN/m para este cálculo.
δ = 0,104 x 90 x 10 6 6.000 2 / (205×10 3 x 478 x 10 6 ) = 1,7 mm
Suponiendo que se utilicen superficies quebradizas
Envergadura / 360 = 6000/360 = 16,7 mm
δ < span / 360, por lo que la deflexión está bien
En el artículo de Wikipedia distracción (tecnología) se explican diferentes métodos para calcular las distracciones.
Capacidad de carga web
Al diseñar vigas de acero, se debe comprobar la capacidad de carga del alma. En esta categoría se prueba la capacidad de carga del alma y el pandeo.
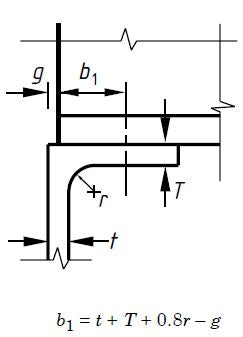
P cabeza = (b 1 + nk) tP Sí
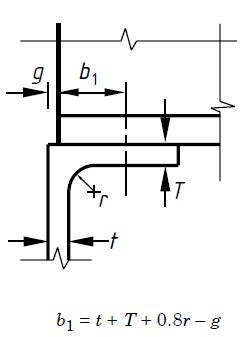
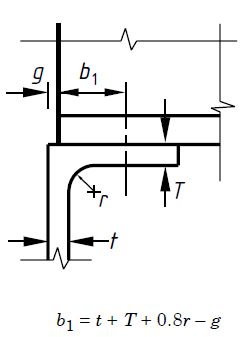
t = 10 mm
T = 10 mm
r = 10 mm
gramos = 5 mm
punto = 5 mm
segundo 1 = t + T + 0,8r – g = 10 + 10 + 0,8 x 10 – 5 = 23 mm
k = T + r = 16 + 20 = 36 mm (para perfil laminado)
al final,
n = (2 + 0,6b t /k) pero ≤ 5
n = (2 + 0,6 x 5/36) = 2,083 < 5 P Sí = 275 N/mm 2 de la Tabla 9
P cabeza = (b 1 + nk) tP Sim = (23 +2.083 x 36) x 10 x 275 x 10 -3 = 269.5kN
La capacidad de carga es de 60 kN.
El soporte del puente está bien y no se necesitan refuerzos.
Si F X >P cabeza tenemos que proporcionar refuerzos para reducir las fuerzas de compensación (F X -P cabeza ). La capacidad de carga de las armaduras viene dada por P S = ON s.net P j . Donde a s.net es el área de la sección transversal de rigidez. Si el alma y la rigidez tienen resistencias diferentes, se debe usar el valor menor para calcular tanto P. S como P cara .
Pandeo del puente
Cuando un t ≥ 0,7 días
P X = 25εt P cabezas /√( ( b 1 + nk) d)
Cuando t <0,7 días
P
Dónde
En t = 0,7d = 23/2 = 11,5 mm <0,7 x 428 = 300 mm
P
PAG
divisas
X
No se necesitan refuerzos.
El listón cumple todas las pruebas.