La no linealidad geométrica es un concepto fundamental en ingeniería que juega un papel crucial en el análisis y diseño de estructuras. A diferencia del análisis lineal, que supone que las estructuras se comportan linealmente bajo carga, la no linealidad geométrica es responsable de las deformaciones causadas por grandes desplazamientos, rotaciones y deformaciones. En este artículo, exploramos el concepto de no linealidad geométrica, su importancia en ingeniería, su impacto en el comportamiento estructural y sus diversas aplicaciones.
En el análisis técnico, a menudo se supone que las estructuras reaccionan linealmente a las fuerzas externas. Sin embargo, en escenarios reales, esta suposición puede no ser cierta cuando se trata de grandes deformaciones o sistemas altamente flexibles. La no linealidad geométrica tiene en cuenta los cambios en la geometría que ocurren como resultado de estas deformaciones, lo que permite una representación más precisa de la respuesta estructural.
Comprender la no linealidad geométrica
La no linealidad geométrica se refiere a la desviación de la linealidad en la geometría de una estructura cuando ésta se somete a cargas o desplazamientos significativos. Esta desviación es provocada por las grandes rotaciones, desplazamientos y deformaciones a las que está sometida la estructura. Es importante considerar la no linealidad geométrica cuando los desplazamientos y las rotaciones se vuelven comparables al tamaño de la estructura o cuando las cargas aplicadas causan deformaciones significativas.
Importancia de la no linealidad geométrica en ingeniería estructural.
La no linealidad geométrica es extremadamente importante en ingeniería por varias razones.
En primer lugar, los ingenieros pueden predecir con precisión el comportamiento de las estructuras sometidas a grandes deformaciones. El análisis lineal no captura los efectos no lineales que pueden provocar fallas inesperadas o catastróficas. Al tener en cuenta las no linealidades geométricas, los ingenieros pueden evaluar de forma más fiable la estabilidad, la resistencia y el rendimiento general de las estructuras.
En segundo lugar, la no linealidad geométrica juega un papel crucial en el proceso de optimización del diseño. Descuidar la no linealidad geométrica puede dar como resultado diseños demasiado conservadores o estructuras propensas a errores. Al tener en cuenta la no linealidad geométrica, los ingenieros pueden optimizar el diseño, reducir el consumo de material y mejorar la eficiencia general de la estructura.
Efectos de la no linealidad geométrica.
La no linealidad geométrica conduce a varios efectos que influyen significativamente en el comportamiento de las estructuras. Estos efectos incluyen:
1. Grandes deformaciones y rotaciones:
Con la no linealidad geométrica, las estructuras pueden sufrir deformaciones y rotaciones importantes. Esto puede provocar cambios en la rigidez, cambios en la distribución de tensiones e inestabilidad potencial.
2. Redistribución de carga:
La no linealidad geométrica puede conducir a la redistribución de carga dentro de una estructura. Cuando se producen deformaciones, las fuerzas y los momentos se redistribuyen, lo que afecta a la estructura general. Respuesta estructural . Además, una capacidad de carga insuficiente del elemento estructural puede provocar fallos estructurales debido al aumento de fuerzas.
3. Comportamiento al pandeo y post-pandeo:
La no linealidad geométrica juega un papel importante en el comportamiento de pandeo y pospandeo de las estructuras. Cuando las deformaciones de una estructura se vuelven grandes, la suposición de pequeños desplazamientos y deformaciones inherentes al análisis lineal ya no es válida. La no linealidad geométrica es responsable de los cambios en la geometría que ocurren cuando una estructura se deforma, lo que resulta en un comportamiento no lineal.
El pandeo es la falla repentina o el colapso de una estructura debido a un equilibrio inestable. La no linealidad geométrica afecta el comportamiento de pandeo al introducir deformaciones adicionales y cambios de forma cuando la estructura alcanza cargas críticas. En un análisis lineal, la carga de pandeo está determinada únicamente por las propiedades del material y la rigidez de la estructura. Sin embargo, en presencia de no linealidad geométrica, la carga crítica también depende de la forma inicial y las condiciones de contorno.
El comportamiento posterior al pandeo describe la reacción de una estructura después del pandeo. La no linealidad geométrica afecta el comportamiento post-pandeo, introduciendo grandes deformaciones y cambios en la rigidez. Después del pandeo, la estructura pasa por una serie de configuraciones de equilibrio a medida que se adapta a nuevas condiciones de carga. El comportamiento posterior al pandeo puede tener formas complejas, deformaciones locales e interacciones entre diferentes tipos de deformaciones.

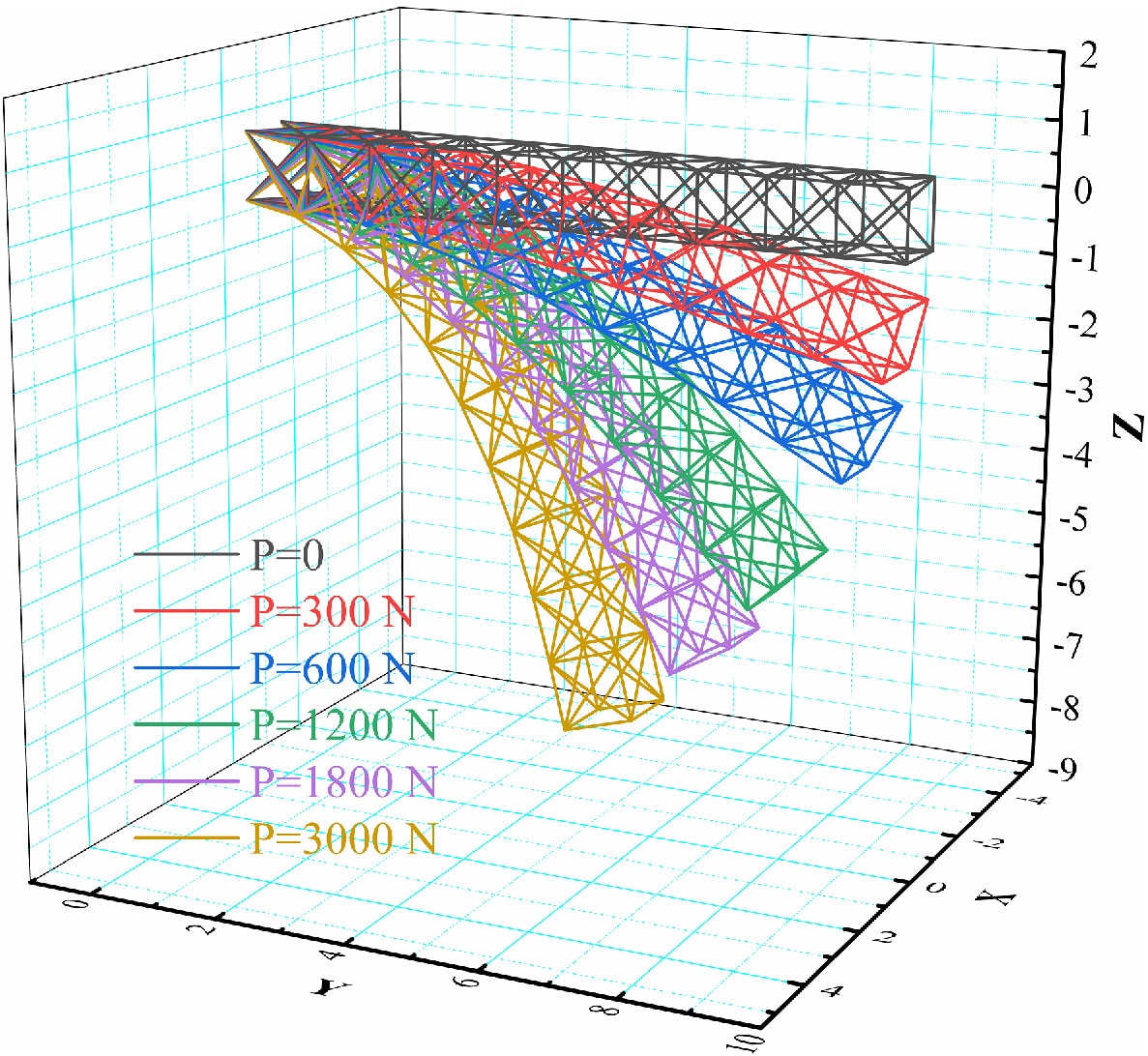
Modelado matemático de no linealidad geométrica.
Los modelos matemáticos se utilizan para analizar y predecir el comportamiento de estructuras bajo no linealidad geométrica. Estos modelos tienen en cuenta las relaciones no lineales entre desplazamientos, rotaciones y cargas aplicadas. El análisis de elementos finitos (FEA) es una técnica ampliamente utilizada para modelar la no linealidad geométrica. FEA discretiza la estructura en elementos pequeños, lo que permite una representación precisa de geometría compleja y comportamiento no lineal.
Se utilizan varios modelos constitutivos para describir la respuesta del material en caso de no linealidad geométrica. Estos modelos tienen en cuenta factores como el endurecimiento, las grandes deformaciones y las relaciones tensión-deformación. Las ecuaciones de equilibrio no lineales se resuelven iterativamente para encontrar los desplazamientos, rotaciones y fuerzas internas que satisfacen las condiciones de equilibrio.
Técnicas de análisis para problemas geométricamente no lineales.
El análisis de problemas geométricos no lineales requiere técnicas especializadas que van más allá del análisis lineal tradicional. Algunas técnicas comúnmente utilizadas son:
1. Métodos iterativos incrementales:
Estos métodos dividen el análisis en pequeños incrementos y resuelven iterativamente las ecuaciones de equilibrio en cada incremento. El enfoque incremental garantiza que los efectos no lineales se capturen con precisión.
2. Control de carga o recorrido:
En el análisis geométrico no lineal, la carga puede controlarse mediante fuerzas aplicadas o desplazamientos prescritos. Esto le permite examinar diferentes escenarios de carga y evaluar la respuesta de la estructura bajo diferentes condiciones.
3. Análisis de pandeo no lineal:
La no linealidad geométrica influye significativamente en el comportamiento de pandeo de las estructuras. El análisis de pandeo no lineal identifica cargas críticas y los modos de falla correspondientes, proporcionando así información sobre la estabilidad estructural.
4. Análisis dinámico:
La no linealidad geométrica puede tener efectos significativos en el comportamiento dinámico de las estructuras. Las técnicas de análisis dinámico, como el análisis modal o el análisis de la historia del tiempo, tienen en cuenta los efectos del comportamiento no lineal en las frecuencias naturales, las formas modales y las respuestas dinámicas.
En resumen, la no linealidad geométrica es un aspecto crucial del análisis de ingeniería que tiene en cuenta las deformaciones y rotaciones que ocurren en estructuras bajo cargas significativas. Es importante comprender y tener en cuenta la no linealidad geométrica para garantizar predicciones precisas del comportamiento estructural y optimizar los diseños.
Aplicaciones de la no linealidad geométrica.
La no linealidad geométrica tiene aplicaciones en varias áreas de la ingeniería. Algunas aplicaciones notables son:
1. Planificación estructural:
La no linealidad geométrica es extremadamente importante en la ingeniería civil. Desempeña un papel importante en el análisis y diseño de estructuras como puentes, edificios y componentes aeroespaciales. Tener en cuenta la no linealidad geométrica ayuda a garantizar la seguridad, la estabilidad y el rendimiento estructurales en condiciones de carga realistas.
2. Ingeniería mecánica:
En ingeniería mecánica, la no linealidad geométrica es crucial para el análisis de mecanismos, componentes mecánicos y sistemas mecánicos. Ayuda a comprender el comportamiento de cuerpos, conexiones y enlaces flexibles, lo que conduce a un mejor rendimiento y confiabilidad.
3. Modelado de materiales:
La no linealidad geométrica está estrechamente relacionada con el comportamiento y la deformación del material. Se utiliza en el modelado de materiales para representar con precisión fenómenos no lineales como la plasticidad, la viscoelasticidad y la hiperelasticidad. Los modelos de materiales con no linealidad geométrica permiten simulaciones y predicciones más realistas.
4. Dinámica de fluidos computacional (CFD):
Las simulaciones CFD a menudo necesitan considerar los efectos de la no linealidad geométrica, particularmente en problemas de interacción fluido-estructura. La no linealidad geométrica influye en el comportamiento de estructuras flexibles en el flujo de fluidos y proporciona información sobre la dinámica y la estabilidad de sistemas como plataformas marinas, turbinas eólicas y alas de aviones.
5. Biomecánica:
La no linealidad geométrica juega un papel importante en el análisis de estructuras biológicas como huesos, tejidos blandos y órganos. Ayuda a comprender la deformación y la respuesta de estas estructuras bajo diferentes condiciones de carga y respalda la investigación médica, el diseño protésico y las simulaciones quirúrgicas.
Preguntas frecuentes
¿Cuál es la diferencia entre análisis geométrico lineal y no lineal?
El análisis lineal supone que las estructuras se comportan linealmente bajo carga, ignorando los efectos de grandes deformaciones y rotaciones. El análisis geométrico no lineal considera las relaciones no lineales entre desplazamientos, rotaciones y cargas aplicadas, lo que permite una representación más precisa del comportamiento estructural.
¿Qué influencia tiene la no linealidad geométrica en la estabilidad estructural?
La no linealidad geométrica puede afectar la estabilidad estructural, provocando pandeo, cambios de formas modales y redistribución de fuerzas y momentos dentro de la estructura. Descuidar la no linealidad geométrica puede conducir a una subestimación de cargas críticas y posibles fallas estructurales.
¿Se puede ignorar la no linealidad geométrica en el análisis de ingeniería?
En muchos escenarios de ingeniería que involucran grandes deformaciones, rotaciones o estructuras flexibles, no se puede ignorar la no linealidad geométrica. Descuidar la no linealidad geométrica puede generar predicciones inexactas, comprometer la seguridad y diseños ineficientes.
¿Existen herramientas de software para abordar problemas geométricamente no lineales?
Sí, existen varias herramientas de software que pueden resolver problemas geométricamente no lineales. Estas herramientas utilizan métodos numéricos avanzados y brindan capacidades para modelado, simulación y análisis de estructuras bajo no linealidad geométrica. Los ejemplos incluyen Abaqus, ANSYS y LS-DYNA.
¿Cuáles son algunos ejemplos de la vida real en los que la no linealidad geométrica juega un papel importante?
Los ejemplos del mundo real donde la no linealidad geométrica juega un papel incluyen el análisis de edificios altos expuestos a cargas sísmicas y de viento, la construcción de puentes y arcos curvos, la simulación de manipuladores robóticos flexibles y el estudio de la mecánica de las válvulas cardíacas en ingeniería biomédica.

