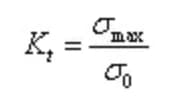Normalmente, as curvas SN obtidas em testes manuais são baseadas nos resultados de amostras padrão sem entalhes. No entanto, as peças reais utilizadas em aplicações do mundo real podem ter diferentes formas, tamanhos, condições de superfície, ambientes de trabalho e características de carga, o que pode impactar significativamente a resistência à fadiga das peças.
Os fatores que afetam a resistência à fadiga podem ser agrupados em três categorias: mecânica, metalurgia e meio ambiente. Esses fatores são interdependentes, tornando difícil avaliar de forma abrangente seu impacto no projeto de resistência à fadiga e na previsão da vida em fadiga.
Fatores mecânicos são influenciados principalmente pela concentração de tensão e pela tensão média. Fatores metalúrgicos estão relacionados à qualidade do material, como pureza e resistência. Os fatores ambientais, por outro lado, incluem a presença de substâncias corrosivas e altas temperaturas.
Para peças de veículos ferroviários, que operam principalmente em condições atmosféricas normais e temperaturas normais, o foco principal deve ser em fatores mecânicos e metalúrgicos, como a influência do formato do entalhe, tamanho, condição da superfície e tensão média.
Informações específicas sobre a influência desses fatores no limite de fadiga podem ser encontradas em manuais e materiais relevantes através do uso de fórmulas empíricas.
Este artigo tem como objetivo discutir as leis e fenômenos importantes que precisam ser compreendidos no projeto de resistência à fadiga e na previsão da vida em fadiga, bem como os cuidados que devem ou deveriam ser levados em consideração.
1. Efeito de forma de entalhe
As peças ou componentes geralmente têm entalhes, como degraus de ressalto, furos de parafusos, furos de óleo, rasgos de chaveta, etc. A característica definidora desses entalhes é que a área da seção transversal das peças sofre uma mudança repentina no entalhe, causando a tensão em a raiz do entalhe aumente significativamente. Este aumento no estresse é conhecido como concentração de estresse.
A concentração de tensão no entalhe é o principal fator responsável pela redução da resistência à fadiga dos componentes. A concentração de tensão faz com que a tensão real na raiz do entalhe seja muito maior que a tensão nominal, levando à formação de trincas por fadiga e eventualmente resultando na falha ou dano da peça.
A extensão da concentração de tensão é descrita pelo fator de concentração de tensão (também conhecido como fator teórico de concentração de tensão) Kt, que é expresso da seguinte forma:

Aqui, σmáx. representa a tensão máxima, e σ0 representa a tensão média calculada dividindo a carga pela área líquida da seção transversal no entalhe, também conhecida como tensão nominal.
Dentro de uma certa faixa, quanto menor o raio de curvatura ρ na raiz do entalhe, maior será a concentração de tensão e maior será a redução na resistência à fadiga. No entanto, para materiais plásticos como aço de baixo e médio carbono, à medida que o raio de curvatura na raiz do entalhe se torna menor e se aproxima de alguns milímetros, a redução na resistência à fadiga torna-se menor ou até deixa de reduzir.
Neste caso, o fator de concentração de tensão não é mais um reflexo preciso do impacto do entalhe na resistência à fadiga. Para refletir com mais precisão a verdadeira redução na resistência à fadiga, o fator de entalhe de fadiga Kf (anteriormente conhecido como fator efetivo de concentração de tensão) é frequentemente usado.

Aqui, σw0 e σw representam os limites de fadiga de corpos de prova lisos sem entalhes e corpos de prova com entalhes, respectivamente.
A figura a seguir ilustra a relação entre o fator de concentração de tensão Kt e o fator de entalhe de fadiga Kf para aço.
Conforme mostrado na figura, para aço de baixo e médio carbono, quando o fator de concentração de tensão é inferior a 2 a 2,5, Kt e Kf geralmente são semelhantes. Porém, quando esse valor é ultrapassado, o aumento de Kf diminui significativamente.
Para aço de alto carbono com alta taxa de resistência, Kf aumenta linearmente com Kt em um longo alcance.
Pode-se concluir que a resistência à fadiga do aço de alta resistência é altamente sensível à presença de entalhes, enquanto a resistência à fadiga do aço de baixa e média resistência é menos sensível aos entalhes.

Geralmente, Kf é menor que Ktmas no caso de entalhes afiados em aço de alto carbono, Kt pode ser maior que Kf. Isto também pode ocorrer em peças de parafusos, onde Kt pode chegar a 4 e Kf pode ser de 8 a 10. Isso se deve à distribuição desigual da carga entre as roscas, com diversas cargas concentradas em uma só rosca.
Para materiais lisos, os tratamentos térmicos de superfície, como têmpera superficial, cementação e nitretação, podem efetivamente melhorar sua resistência à fadiga. No entanto, estes métodos podem ser ineficazes ou até mesmo reduzir a resistência à fadiga dos materiais entalhados. Isto ocorre porque a resistência superficial é melhorada através do tratamento térmico, mas a sensibilidade aos entalhes também aumenta.
A figura a seguir ilustra a mudança na resistência à fadiga do aço entalhado de alta resistência e do aço de baixa resistência com boa plasticidade à medida que a concentração de tensão aumenta. Na faixa de menor concentração de tensão Kt, a resistência à fadiga do aço de alta resistência é significativamente maior do que a do aço de baixa resistência. No entanto, à medida que o fator de concentração de tensão aumenta, a resistência à fadiga do aço de alta resistência diminui mais rapidamente do que a do aço de baixa resistência, resultando na resistência à fadiga do aço de alta resistência sendo quase igual à do aço de baixa resistência.

Para componentes soldados, a resistência à fadiga é muitas vezes significativamente reduzida devido à combinação da zona afetada pelo calor estar localizada perto do entalhe estrutural e à presença de defeitos de soldagem e tensão de tração residual. Essa redução pode ser várias vezes maior que o normal ou até mais de dez vezes.
O coeficiente de entalhe de fadiga também pode ser afetado pelo tamanho das peças. Como regra geral, para o mesmo entalhe, o coeficiente de fadiga do entalhe aumenta com o aumento do tamanho.
Para melhorar a vida à fadiga de materiais entalhados ou componentes com entalhes, é mais eficaz realizar o projeto estrutural e a seleção de processos que reduzam ou melhorem a concentração de tensões.
No entanto, uma superfície rugosa e de tamanho grande pode reduzir a resistência à fadiga dos componentes.
2. Efeito de tamanho das peças
O diâmetro da amostra usada para testes de fadiga é normalmente entre 5 e 10 mm, o que é muito menor que o tamanho real das peças.
Para componentes sujeitos a cargas de flexão e torção, a resistência à fadiga diminui à medida que o tamanho aumenta. Contudo, para cargas de tensão axial e compressão, o tamanho tem um efeito mínimo.
A influência do tamanho no limite de fadiga é representada pelo coeficiente de influência do tamanho (ε).

Aqui, σd e σd0 representam os limites de fadiga de amostras lisas de qualquer tamanho e tamanho padrão, respectivamente.
O efeito do tamanho no aço de alta resistência é maior do que no aço de baixa resistência, e o efeito do tamanho é mais pronunciado para peças com superfícies rugosas.
O efeito do tamanho é principalmente devido ao impacto do estado da estrutura do material e do gradiente de tensão na resistência à fadiga de componentes maiores.
À medida que o tamanho do material aumenta, torna-se mais difícil controlar o processo de fabricação, e a estrutura do material torna-se menos uniforme e compacta, com mais defeitos metalúrgicos e uma área superficial maior, o que aumenta a probabilidade desses defeitos.
Isso resulta em um maior risco de fadiga e rachaduras na superfície de amostras grandes. A concentração local de tensões causada por defeitos metalúrgicos leva à formação de trincas por fadiga.
Em relação à influência do gradiente de tensão, quando submetido a flexão, torção e outras cargas, quanto maior o tamanho do componente, menor o gradiente de tensão de trabalho, maior a tensão média por unidade de área e mais fácil é a fadiga rachaduras se formarão.
3. Efeito da condição da superfície
As condições da superfície afetam vários fatores, como rugosidade da superfície, estado de tensão da superfície, grau de deformação plástica da superfície, defeitos superficiais e outros.
No processo de teste, é utilizada a amostra padrão com superfície polida, porém, as peças reais geralmente possuem superfícies usinadas, forjadas ou fundidas.
A usinagem pode resultar no endurecimento do plástico na superfície da peça.
O corte muitas vezes deixa tensões de compressão residuais na superfície, o que melhora a resistência à fadiga, mas apenas até certo ponto.
A retificação, por outro lado, pode causar tensão de tração residual, o que é prejudicial à resistência à fadiga.
Além disso, a rugosidade em microescala das superfícies usinadas pode levar à concentração de tensões e diminuir a resistência à fadiga.
O efeito combinado destes fatores resulta em uma menor resistência à fadiga em comparação com a amostra padrão.
Superfícies forjadas ou fundidas normalmente apresentam maior rugosidade e camadas de endurecimento superficial, bem como tensões residuais de compressão, levando a uma diminuição significativa na resistência à fadiga.
Concluindo, quanto mais rugoso for o método de processamento da superfície, maior será o seu impacto na redução da resistência à fadiga.
O efeito das condições de processamento superficial na resistência à fadiga é representado pelo coeficiente de processamento superficial (β).

Aqui, σβ representa o limite de fadiga de uma amostra lisa padrão em um determinado estado de superfície, σβ0 representa o limite de fadiga de uma amostra lisa padrão polida e “no exterior” refere-se à amostra lisa padrão com superfície polida.
Do ponto de vista metalúrgico, a usinagem em desbaste tem um impacto significativo na resistência à fadiga de materiais de alta resistência; portanto, o aço de alta resistência pode não aumentar a resistência à fadiga em estados de usinagem em desbaste. Isso se deve principalmente à alta sensibilidade do entalhe dos materiais de alta resistência às superfícies ásperas e ao mínimo efeito de endurecimento da usinagem na superfície do aço de alta resistência.
Poucas pesquisas foram feitas sobre o impacto de defeitos superficiais, como descarbonetação superficial, marcas de colisão superficial e arranhões, na resistência à fadiga. No entanto, defeitos superficiais causados por motivos acidentais podem ter um impacto significativo na resistência à fadiga. Portanto, atenção suficiente deve ser dada a estas questões no projeto e especialmente no processo de fabricação.
Para materiais lisos, o tratamento térmico de superfície e outros métodos de modificação de superfície podem melhorar a resistência à fadiga. No entanto, para materiais com entalhes, como peças reais, estes métodos têm pouco efeito e podem até ter um efeito adverso. Como resultado, shot peening e laminação são frequentemente usados para gerar endurecimento por trabalho e tensão de compressão residual na superfície, melhorando assim a resistência à fadiga dos componentes.
No entanto, estes dois métodos geralmente não melhoram significativamente a resistência à fadiga de peças com furos. As pesquisas mais recentes mostram que o uso de uma matriz de metal simples para chanfrar uma pequena parte da borda do furo pode melhorar significativamente a resistência à fadiga e até mesmo eliminar o impacto do entalhe, reduzindo o limite de fadiga.
No passado, acreditava-se comumente que a principal razão para a melhoria na resistência à fadiga dos métodos de processamento de superfícies plásticas era devido à tensão de compressão residual gerada na superfície compensando parte da tensão de trabalho.
No entanto, a tensão compressiva concentrada produzida pela tensão compressiva residual no entalhe compensou o efeito adverso do entalhe. A deformação plástica fortalece as áreas fracas próximas ao entalhe, tornando a estrutura mais uniforme e melhorando a resistência geral, o que por sua vez melhora o nível de tensão que produz trincas por fadiga.
Além disso, a tensão residual de compressão faz com que as fissuras por fadiga parem de crescer e se tornem fissuras permanentes.
4. Efeito do estresse médio
Como afirmado anteriormente, a principal causa da falha por fadiga é a tensão dinâmica, mas o componente de tensão estática, ou tensão média, também tem algum impacto no limite de fadiga. Numa gama específica de tensão estática, um aumento na tensão estática de compressão aumentará o limite de fadiga, enquanto um aumento na tensão estática de tração irá reduzi-lo.
É amplamente aceito que a tensão residual tem um efeito semelhante no limite de fadiga que a tensão média. Para um determinado material, um diagrama de limite de fadiga pode ser traçado com base em seus resultados de limite de fadiga sob diferentes tensões médias ou taxas de tensão (R).
O diagrama abaixo apresenta uma quantidade adimensional, a razão entre a tensão média (σeu) ou tensão residual, até o limite de resistência (σb), no eixo x, e a razão da amplitude de tensão (σa) ao limite de fadiga cíclica simétrica (σ-1), no eixo y.

A figura mostra que a maioria dos pontos de dados de teste ficam entre linhas retas e curvas. A linha reta é chamada de linha de Goodman, enquanto a curva é conhecida como parábola de Gerber. A linha de Soderberg é obtida substituindo o limite de resistência (σb) com o limite de rendimento (σé). Da mesma forma, a linha de Morrow é derivada substituindo σb pela verdadeira tensão de fratura (σf).
Linha Goodman:

Linha Gerber:

Linha Soderberg:

Linha amanhã:

A linha Goodman é uma abordagem conservadora e direta para metais dúcteis, tornando-se um método amplamente utilizado em projetos de fadiga. Outro método frequentemente usado é o Diagrama Ideal Melhorado de Goodman.
A figura a seguir ilustra o diagrama de Goodman ideal melhorado de uma viga de aço em forma de I sob carga de fadiga por flexão. O eixo x representa a tensão mínima (σmin), o eixo y representa a tensão máxima (σmáx.), e a equação linear é a seguinte:

Onde m é a inclinação da linha de Goodman, b é a interceptação da linha no eixo y e é o limite de fadiga do ciclo de pulsação quando a tensão mínima é igual a zero.
Quando o limite de fadiga é expresso pela tensão máxima, nomeadamente σ c= σ Máx.considerando a razão de tensão R= σ máx./σ Mínimo.
A linha Morrow inclui:


O limite de fadiga para uma determinada relação de tensão (R) pode ser calculado usando a fórmula acima. Porém, a estrutura real de um veículo é muito mais complexa do que as condições de teste sob as quais a curva SN foi obtida, como o tipo de soldagem e as concentrações de tensões.
A norma americana AAR fornece orientações valiosas para a resistência à fadiga de várias estruturas de soldagem e, portanto, os valores de “b” e “m” nos cálculos reais são retirados da norma AAR.
Os resultados dos testes indicam que o impacto dos componentes da carga estática no coeficiente de concentração de tensão, no coeficiente de dimensão e no coeficiente de superfície é menor e pode ser desconsiderado.