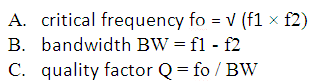Existem 2 frequências de corte para filtro passa-banda.
1. frequência de corte superior (f1) – a frequência abaixo da qual todas as frequências são passadas
2. frequência de corte inferior (f2) – todas as frequências acima desta frequência são passadas
A partir destes f1 e f2 definiremos os seguintes parâmetros que estão projetando parâmetros para filtro passa-banda.

Fig.1: Captura de tela listando diferentes parâmetros para filtro passa-banda
Com base em Q temos dois tipos de filtro passa-banda
1. Filtro passa banda larga – com Q <10 tem ampla resposta plana em toda a faixa de frequências. BW é mais
2. Filtro passa banda estreita – com Q>10 tem uma resposta nítida do tipo sino. BW é muito menor.
Filtro passa banda larga
Na verdade, é uma combinação de LPF e HPF, conforme mostrado na figura

Fig. 2: Visão geral do filtro passa-banda larga
Aqui F2 > F1. Então temos que projetar HPF com F1 e LPF com F2. Suponha que queiramos passar a banda de frequências entre 2 KHz a 5 KHz. então F1 = 5.000 Hz e F2 = 2.000 Hz.
Projetando seção HPF
Passo 1: assuma o valor necessário do capacitor. Deve ser inferior a 0,1 micro Farad. Isso é necessário para uma melhor estabilidade de frequência. Suponha que assumimos o valor C como 10 nF (nano farad)
Passo 2: calcule o valor da resistência da equação

Fig. 3: Captura de tela dos cálculos necessários para encontrar a resistência do HPF no filtro passa-banda larga

Figura 4:
portanto, nossa suposição para o valor de capacitância como 10 nF é boa (ou OK). Caso contrário, se o valor calculado de R for muito menor que 1 KOhm, teremos que assumir algum outro valor do capacitor. Porque o valor de R não deve ser inferior a 1 K Ohm.
Etapa 3: escolha o ganho de banda passante necessário. Suponha que tomemos isso como 2. Então forme a equação
Af = 1 + (R2/R1)
2 = 1 + (R2/R1)
R2/R1 = 1
R2 = R1

Figura 5: Captura de tela dos cálculos necessários para encontrar a resistência do HPF no filtro passa-banda larga
Projetando seção LPF
Passo 4: assuma o valor necessário do capacitor. Suponha que assumimos o mesmo valor C como 10 nF
Etapa 5: calcule o valor da resistência da equação

Figura 6: Captura de tela dos cálculos necessários para encontrar a resistência do LPF no filtro passa-banda larga
Este valor é um valor ímpar do resistor. Pode não estar disponível como valor fixo. Então podemos usar potenciômetro de 4,7 K? e ajuste-o ao valor desejado.
Etapa 6: escolha o ganho de banda passante necessário. Se considerarmos isso como 2, então novamente
R2 = R1

Fig. 7: Captura de tela dos cálculos necessários para encontrar a resistência do LPF no filtro passa-banda larga
O projeto final com os valores dos componentes são mostrados. O amplificador operacional é um componente ativo e requer tensões de polarização +ve e -ve. Pode-se testar o circuito aplicando a entrada através do gerador de sinal e observando a saída no DSO ou osciloscópio, bem como no plotter de bode, conforme mostrado na figura.
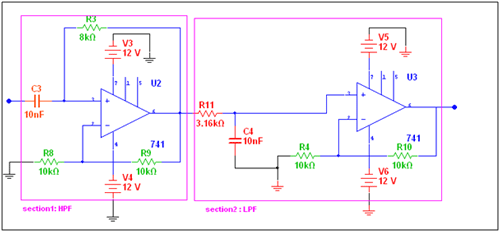
Fig. 8: Diagrama de circuito do filtro passa-banda larga baseado em IC LM741 OPAMP
Observação: – O projeto esquemático é preparado no software multisim 11 da NI. O software está disponível gratuitamente por um período de teste de 1 mês no site da NI. A seguir todos os circuitos também são preparados no software multisim 11.
Filtro de passagem de banda estreita
Passo 1: para simplificar, assuma C1 = C2 = C
Passo 2: selecione frequência central fc = 2 KHz, ganho de banda passante Af = 2 e Q = 10
Etapa 3: assuma o valor do capacitor C como 100nF
Passo 4: calcular o valor de R1 de

Fig. 9: Captura de tela dos cálculos necessários para encontrar a resistência do filtro passa-banda estreita
O design final é mostrado abaixo.

Fig. 10: Diagrama de circuito do filtro passa-banda estreita baseado em IC LM741 OPAMP