Este artigo explica o dimensionamento de pilares de aço de acordo com o Eurocode 3, EN 1993-1-1, utilizando um exemplo prático. As explicações do projeto são feitas consultando as seções relevantes do Código.
Para uma explicação detalhada da estrutura de suporte de aço, consulte o artigo Projeto de coluna de aço de acordo com o Eurocode 3.
O processo de design descrito no artigo acima é o seguinte.


Vamos começar o processo de design com um exemplo prático.
Dados de design
- Dimensões da coluna 150x150x 31,1 kg/m
- Classe de aço S275
- Altura da coluna 3m
- Carga axial 500 kN
- Por uma questão de simplicidade, neste exemplo consideramos a coluna com uma extremidade de pino
Classificação da seção
Vamos descobrir os parâmetros de força.
t < 40 mm
Da Tabela 3.1 da EN 1993-1-1,
fy = 275 N/mm2
ε = √(235/fj) = √(235/275) = 0,92
Da seção 6.1:
γm0 = 1,0
γm1 = 1,0
A = 39,65cm2
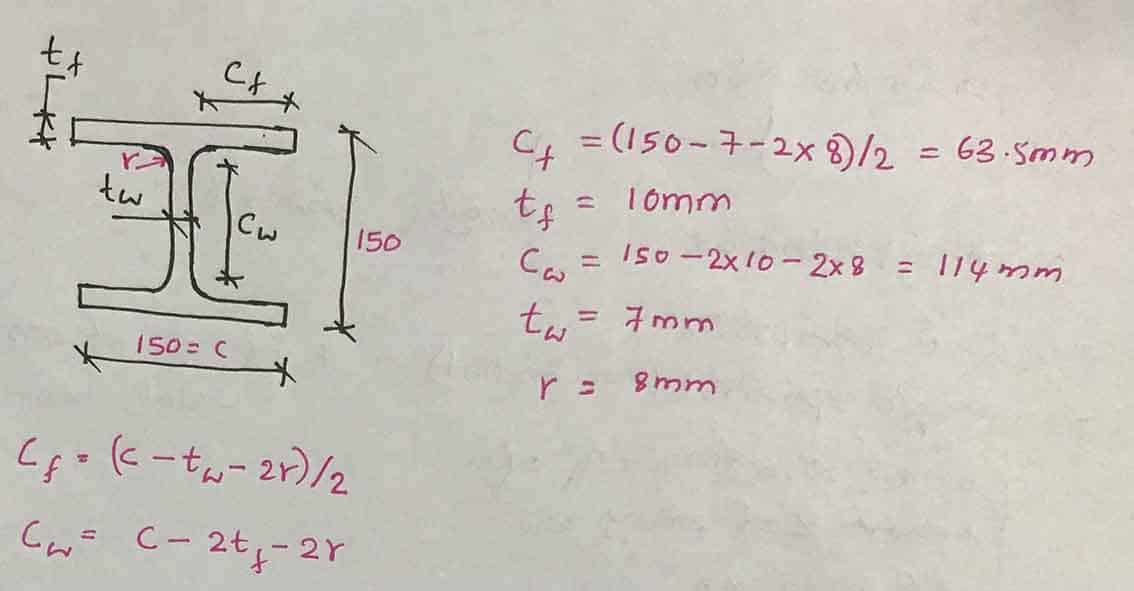
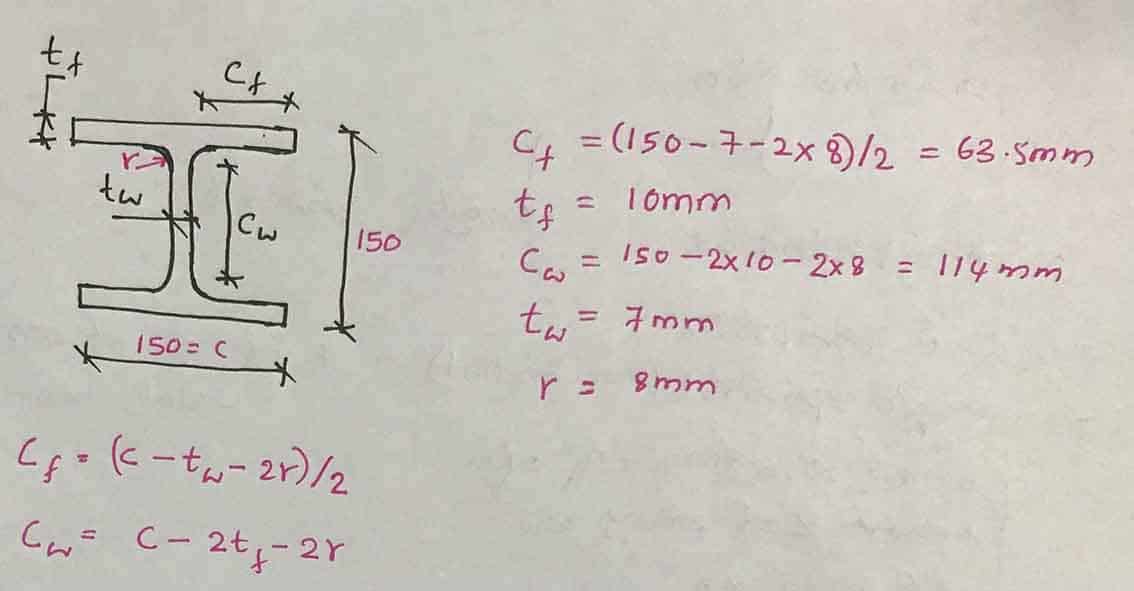
Podemos calcular os limites de magreza.
mesa
CF/TF = 63,5/10 = 6,35 < 9ε = 9 x 0,92 = 8,82; Seção classe 1
rede
Ceu/Teu = 114/7 = 16,3 < 33ε = 33 x 0,92 = 30,36; Seção classe 1
-
Resistência plástica ou resistência transversal, Nc, Estrada
- Perfis não finos: Classe 1
Nc,Rd = Afj /γm0 = 3965 x 275/1 = 1.090,4 kN
Após calcular a resistência, deve ser realizado o seguinte teste de capacidade.
NEd. = 500 kN
NEd. /Nc,Rd = 500/1090,4 = 0,46 <1
A seção transversal atende à resistência plástica.
- Resistência à flambagem, Nb, Estrada
Primeiro calcule a resistência à encurvadura dependendo da classe da secção.
Vamos seguir o procedimento no processo de design.
λ1 = 93,9ε = 93,9 x 0,92 = 86,4
Ao projetar o pilar, precisamos considerar a resistência em torno de cada eixo (YY e ZZ).
i = raio de giração
EUJJ = 6,4 cm
EUatualmente = 3,77cm
Mcr = comprimento de flambagem
Como as duas extremidades da coluna estão fixadas,
Mcr = 1,0 x L = 3m
λ¯ = eucr / euλ1
Eixo YY; λ¯ = eucr / euλ1 = 3000 / (64 x 86,4) = 0,54
Eixo ZZ; λ¯ = eucr / euλ1 = 3000 / (37,7 x 86,4) = 0,92
Vamos determinar o α – fator de imperfeição da Tabela 6.1 da EN 1993-1-1
Encontre a curva de flambagem
h/b = 150/150 = 1 < 1,2
TF = 10 mm < 100 mm
Vejamos agora a parte da tabela 6.2 da EN 1993-1-1,
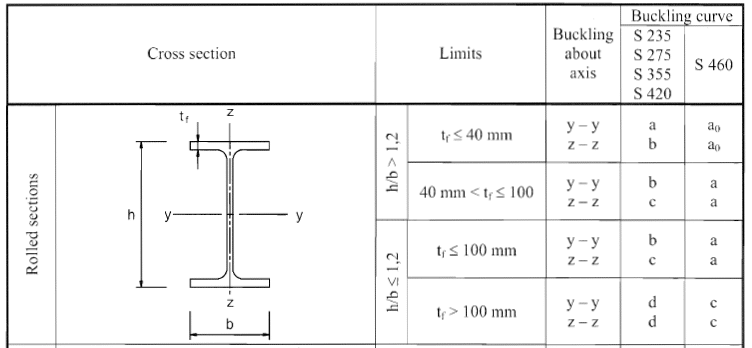
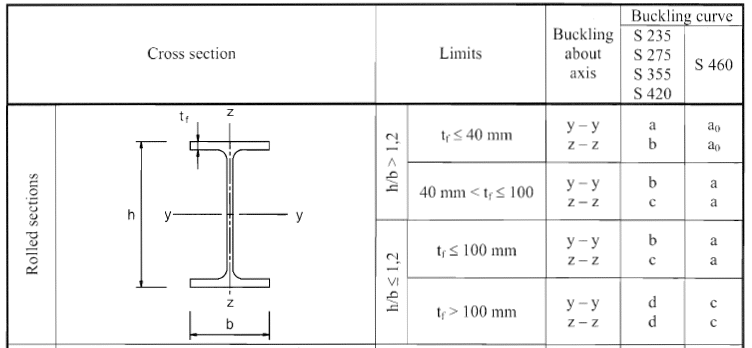
Portanto, a curva jubarte resulta da seguinte forma
Eixo YY – b
Eixo ZZ – c
Da Tabela 6.1
| Curva de curvatura | A0 | A | b | C | D |
| Fator de imperfeição α | 0,13 | 0,21 | 0,34 | 0,49 | 0,76 |
α no eixo YY = 0,34
α no eixo ZZ = 0,49
Agora calcule Ø
Ø = 0,5 ( 1 + α( λ¯ – 0,2) + λ¯2)
Sobre o eixo YY
Ø = 0,5 (1 + 0,34(0,54 – 0,2) + 0,542) = 0,7
Sobre o eixo ZZ
Ø = 0,5 (1 + 0,49(0,92 – 0,2) + 0,922) = 1,1
Cálculo do fator de redução, χ
χ =1 /( Ø + √(Ø2 –λ¯2 )) ≤ 1,0
Sobre o eixo YY
χ =1 /( 0,7 + √(0,72 – 0,542 )) = 0,873 < 1,0
Sobre o eixo ZZ
χ =1 /( 1,1 + √(1,12 – 0,922 )) = 0,587 < 1,0
O χ mais baixo é o eixo crítico contra a flambagem e menor resistência à flambagem está disponível.
Portanto,
χ = 0,587
Agora calcule a resistência à flambagem Nb, Estrada,
Nb, Estrada = χ A fj /γM1 – Não é magro – Classe 1
Nb, Estrada = 0,587 x 3965 x 275/1 = 640 kN
- Verificação de capacidade
NEd. /Nb, Estrada ≤ 1,0
NEd. /Nb, Estrada = 500/640 = 0,781 <1
A seção está ok.
Para mais informações, consulte o artigo “Eurocode 3: Projeto e construção de estruturas metálicas” publicado na Wikipedia.

