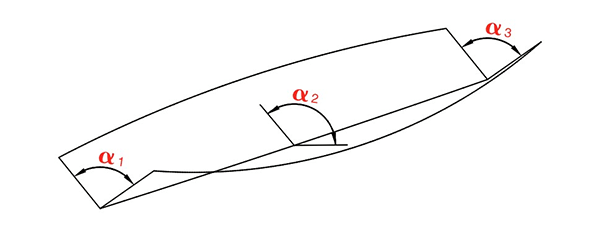
Precisão de Dobra
Erro de ângulo e erro de retidão
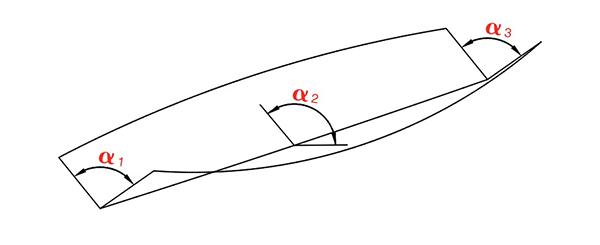
Pergunta: existe erro de ângulo e erro de retilineidade no “estado de flexão ideal”?
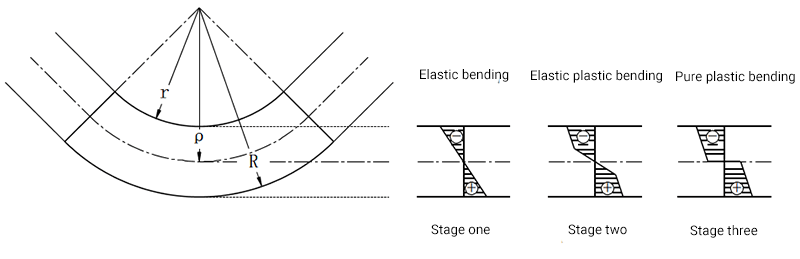
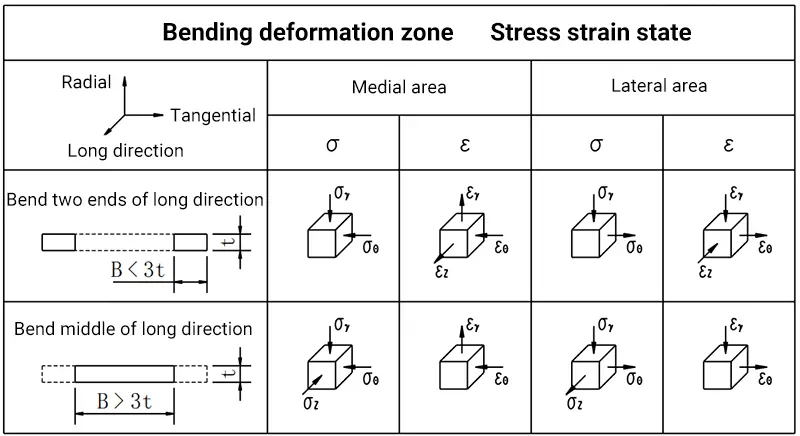
Análise de tensão e deformação do processo de dobra de chapa metálica
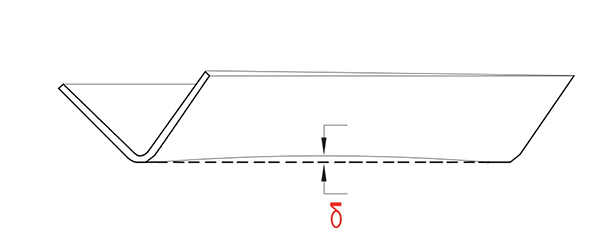
Análise de erro de retidão
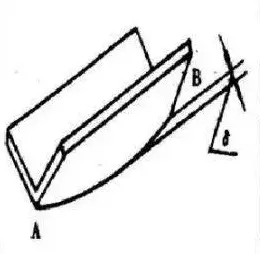
Após a dobra da chapa metálica, a borda da peça dobrada apresentará deflexão natural, que normalmente é medida pela sua deflexão máxima (δ).
De acordo com a análise de tensões, a tensão (σZ) na zona de deformação é de tração externa e compressiva internamente. Essas tensões opostas de tração e compressão criam um momento fletor, que é necessário para manter a peça reta durante a flexão. Porém, ao final do processo de dobra, esse momento desaparece, fazendo com que a peça se desvie para cima.
Quanto mais longa for a placa de dobra, maior será a deflexão (δ). Da mesma forma, quanto mais larga for a placa dobrada, quanto menor for a largura da placa, maior será a deflexão (δ).
No entanto, reduzir o ângulo de curvatura de 150° para 90° reduzirá a deflexão (δ).
Além disso, à medida que a espessura da placa aumenta, a deflexão (δ) aumentará proporcionalmente.
Aplicar pressão na borda da folha dobrada, como por meio de dobra de correção ou dobra de três pontos, pode melhorar a retilineidade da peça de trabalho.
Fatores que afetam a precisão da flexão
Os principais fatores que influenciam a precisão da dobra em uma máquina dobradeira são a rigidez da dobradeira, o modo de dobra e a força de dobra.
1. Pressione a rigidez do freio
Como determinar o índice de rigidez da máquina dobradeira no projeto?
Deformação por deflexão de pressione o freio máquina

2. Modo de flexão
1) Dobragem de ar
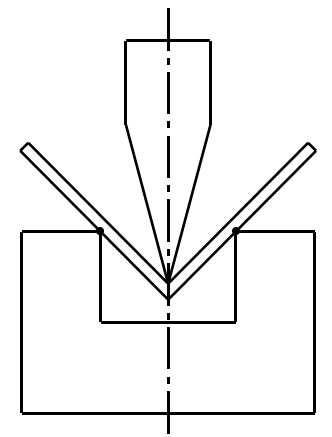
2) Flexão de três pontos
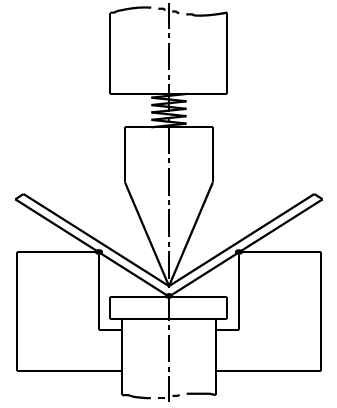
3) Cunhagem
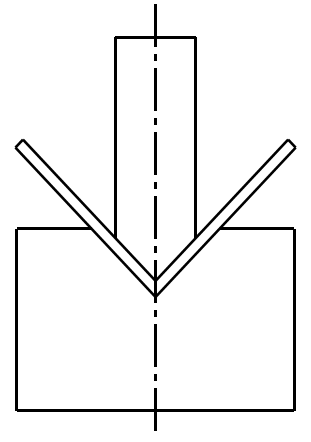
3. Força de flexão
Como a força de flexão muda durante a flexão?
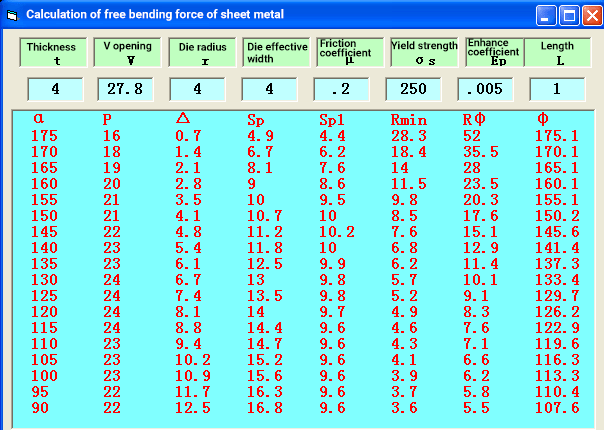
1)Flexão livre do soco agudo
Conforme ilustrado na figura anexa, no modo de flexão livre, o material da chapa é feito de aço Q235, que é considerado como tendo comportamento elástico-plástico ideal com endurecimento linear. A resistência ao escoamento deste material é σS = 250 MPa, e seu módulo de endurecimento (também conhecido como módulo tangente) é 1050 MPa.
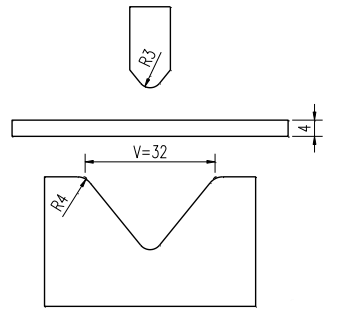
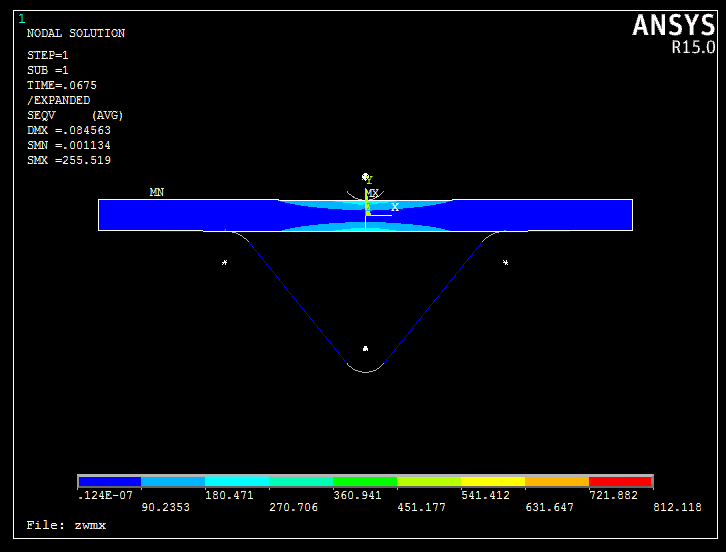
Os resultados da análise ANSYS são os seguintes
Curva de força de flexão:
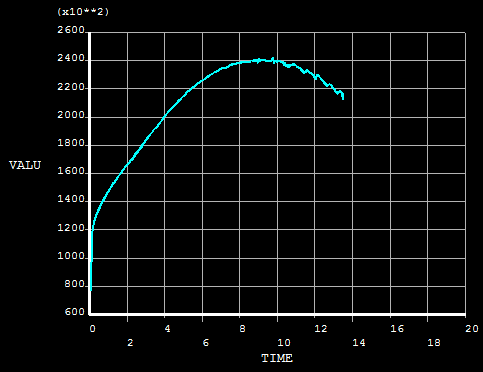
Os resultados do método analítico são os seguintes
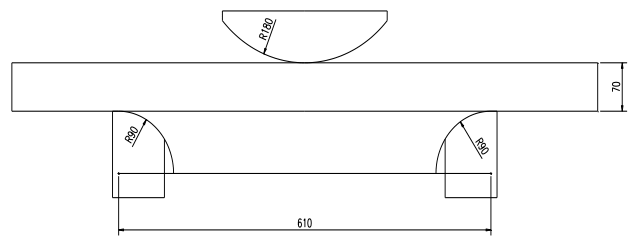
2) Dobragem larga da faca
Conforme ilustrado na figura anexa, a matriz superior é projetada com um amplo arco R180 e o material da folha é definido como X80. Este material possui comportamento elástico-plástico ideal com endurecimento linear e seu limite de escoamento é σs = 552 MPa. O módulo de endurecimento (também conhecido como módulo tangente) deste material é de 840 MPa.
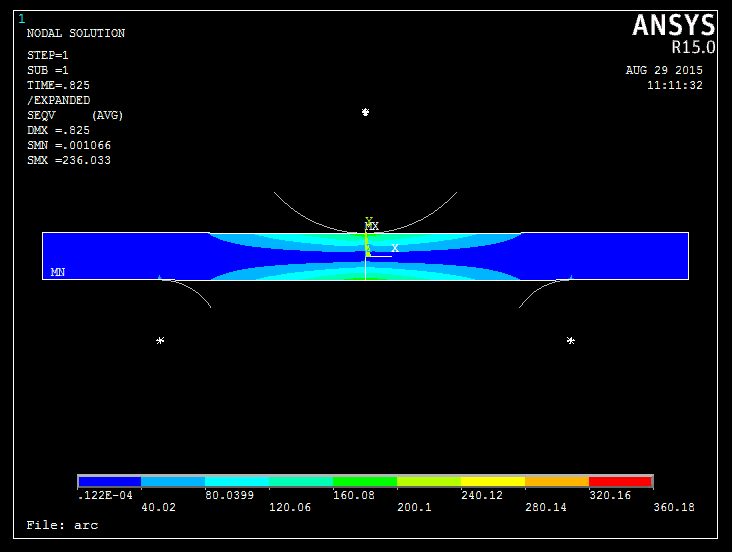
Os resultados da análise ANSYS são os seguintes
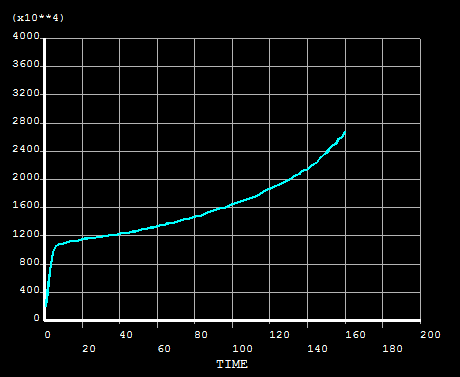
Curva de força de flexão:
Existem outros fatores que afetam a precisão da dobra, entre os quais estão a espessura irregular da placa, a dureza da placa, a deformação da bancada e do aríete durante a dobra, a seleção da abertura da matriz, a profundidade da matriz superior na matriz inferior, o desgaste da matriz e a convexidade da bancada. Esses fatores podem causar erros no ângulo de flexão e na retilineidade da peça após a flexão.
A abertura da matriz e a profundidade da matriz superior na matriz inferior são controladas por programação manual.
4. Influência da qualidade do material na precisão
A dobra nominal é uma dobra livre de chapa de aço de baixo carbono com resistência à tração σb = 450 N/mm², que dobra a chapa em um ângulo de 90° na matriz em forma de V com uma distância de abertura V = 8 × S.
Quando a flexão nominal é realizada com placas de espessura irregular, podem ocorrer erros de ângulo.
Quando a dureza da placa não é uniforme, o retorno elástico da peça durante a flexão não é igual.
Portanto, a qualidade dos materiais tem um impacto significativo na qualidade do processamento.
5. Compensação convexa da mesa de trabalho
Sob a ação da carga, a bancada e o aríete sofrerão deformação elástica.
A profundidade da matriz superior na matriz inferior é irregular ao longo de todo o comprimento, o que pode afetar o ângulo de curvatura e a retilineidade da peça de trabalho.
Para resolver este problema, a máquina adota o NC convexo da mesa de trabalho para compensar sua deformação, manter a profundidade da matriz superior na matriz inferior essencialmente uniforme ao longo de todo o comprimento e melhorar a precisão do ângulo de flexão e da retilineidade do peça de trabalho.
6. Carga excêntrica
Carga excêntrica refere-se à operação de carga no lado esquerdo ou direito do aríete. A máquina tem uma forte capacidade de resistir a cargas excêntricas.
Sob a ação da força de carga excêntrica, será gerada inclinação entre a bancada e o aríete.
O mecanismo de detecção de grade em ambas as extremidades do aríete detectará o desvio e fornecerá feedback ao computador. O computador controla a servoválvula proporcional para ajustar a quantidade de óleo que entra no cilindro de óleo, para manter a posição dos dois pistões sincronizada e manter um pequeno erro de paralelismo entre a bancada e o aríete.
Ao processar peças especiais, deve-se considerar a carga excêntrica acima. Em geral, é necessário evitar operar sob carga excêntrica.
7. Correção de erro de ângulo de flexão
Após a parte dobrada ter sido formada e o ângulo ser de cerca de α°, o valor de erro do ângulo medido △α° pode ser corrigido ajustando a posição Y do ponto morto inferior. O valor de correção △Y pode ser calculado aproximadamente de acordo com a seguinte fórmula: △Y = K × V × △α
Onde:
- △ Y – valor de correção do ponto morto inferior (mm)
- V – abertura selecionada da matriz (mm)
- △ α – Valor do erro do ângulo (graus)
- K – Fator de correção (grau /mm)
Quando α ≈ 90°, K ≈ 0,0055; para barra de aço dobrada de 8-12 lados, quando α ≈ 135°-157,5°, K ≈ 0,004.
Se o ângulo da peça inspecionada for maior que os requisitos do desenho, ajuste a posição do ponto morto inferior para baixo de acordo com o valor de correção △Y; caso contrário, ajuste para cima.
Exemplo 1:
Os ângulos em ambas as extremidades são iguais ao ângulo médio.
Para dobrar um dodecágono com α= 150°, selecione a abertura V = 200mm, e meça o ângulo após a dobra, α= 151,5°. Usando o método acima, △α é calculado como 1,5° e K é 0,004.
△Y = K × V × △α = 0,004 × 200 × 1,5 = 1,2 mm.
Insira a posição do ponto morto inferior Y + △Y no computador.
Exemplo 2:
Os ângulos em ambas as extremidades não são iguais ao ângulo médio.
Para uma peça dobrada em α=90° com abertura V = 60mm, os ângulos reais medidos em ambas as extremidades são α=90°, e o ângulo médio é α=91° (a quantidade convexa não é suficiente).
Usando o método acima: △α = 1°; K=0,0055
△Y = K × V × △α = 0,0055 × 60 × 1 = 0,33 mm.
Adicione △Y ao valor convexo original e insira-o no computador.
Se o ângulo médio for menor que os ângulos em ambas as extremidades (a quantidade convexa é muito grande), reduza o valor convexo em △Y da base original e insira-o no computador.
Exemplo 3:
Os ângulos nas extremidades inferiores da coluna não são iguais. Com largura de abertura V = 60mm, uma peça é dobrada em α= 90°.
O ângulo real medido na extremidade esquerda é α=90°, e o ângulo na extremidade direita é α=91° (inferior esquerdo e superior direito).
Usando o método acima: △α=1, K=0,0055
△Y=K × V × △α=0,0055 × 60 × 1=0,33 mm
Insira o valor Y + △Y no ponto zero da extremidade direita para cima para alterar sua posição de referência.
8. Precisão do ângulo
A precisão do ângulo é sem dúvida o parâmetro mais complexo e desafiador para controlar em operações de dobra. Existem dois métodos de dobra comuns: dobra de fundo e dobra de ar. Várias aplicações de flexão de fundo são ilustradas a seguir.
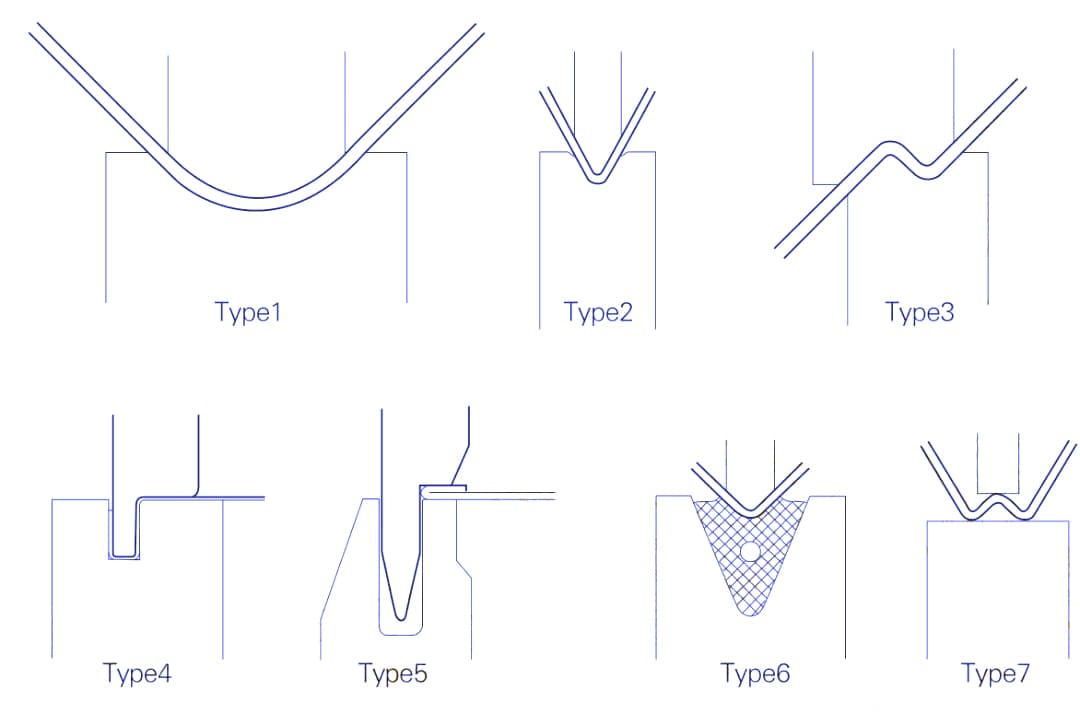
A flexão de fundo é controlada ajustando a força descendente aplicada durante o processo de flexão para moldar o metal. Suas vantagens incluem alta precisão angular, atingindo até ±15 minutos, com ângulos de curvatura consistentes.
No entanto, as desvantagens são significativas: requer até cinco a oito vezes mais força do que a flexão a ar e tem menor flexibilidade. Diferentes ângulos ou formas requerem ferramentas diferentes.
A flexão a ar, também conhecida como flexão livre, é mais comumente usada. É controlado regulando a descida do eixo Y, ou seja, a profundidade em que a matriz superior penetra na matriz inferior, controlando assim o ângulo de curvatura.
As vantagens da dobra a ar incluem menor força necessária e alta flexibilidade, já que um conjunto de ferramentas pode dobrar peças em vários ângulos. A desvantagem é a menor precisão no ângulo da peça dobrada e a menor consistência.
Por que a precisão do ângulo das peças dobradas a ar é menor? Por exemplo, ao dobrar chapa metálica com uma matriz inferior V10, uma diferença de 0,05 mm na distância que a matriz superior pressiona pode resultar em um desvio angular de 1°, conforme mostrado na tabela abaixo.
Tabela: Mudanças na profundidade de descida correspondente a uma variação de ângulo de 1° para diferentes aberturas inferiores da matriz e ângulos de curvatura
| Ângulo de curvatura/abertura inferior do molde | 30° | 45° | 60° | 75° | 90° | 105° | 120° | 135° | 150° | 165° |
| 4 | 0,17 | 0,07 | 0,04 | 0,03 | 0,02 | 0,02 | 0,02 | 0,01 | 0,01 | 0,01 |
| 6 | 0,26 | 0,11 | 0,07 | 0,05 | 0,04 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 |
| 8 | 0,36 | 0,14 | 0,08 | 0,06 | 0,05 | 0,04 | 0,04 | 0,03 | 0,03 | 0,03 |
| 9 | 0,41 | 0,16 | 0,09 | 0,07 | 0,05 | 0,05 | 0,05 | 0,04 | 0,03 | 0,03 |
| 10 | 0,45 | 0,18 | 0,10 | 0,08 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,04 |
| 12 | 0,54 | 0,22 | 0,13 | 0,08 | 0,07 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 |
| 14 | 0,61 | 0,24 | 0,15 | 0,10 | 0,08 | 0,07 | 0,06 | 0,06 | 0,06 | 0,06 |
| 15 | 0,66 | 0,26 | 0,16 | 0,11 | 0,08 | 0,08 | 0,07 | 0,07 | 0,07 | 0,06 |
| 16 | 0,71 | 0,28 | 0,16 | 0,12 | 0,09 | 0,08 | 0,07 | 0,07 | 0,07 | 0,07 |
| 18 | 0,81 | 0,32 | 0,19 | 0,13 | 0,11 | 0,09 | 0,08 | 0,08 | 0,07 | 0,07 |
| 20 | 0,90 | 0,36 | 0,21 | 0,15 | 0,11 | 0,10 | 0,09 | 0,09 | 0,09 | 0,08 |
| 22 | 1,00 | 0,40 | 0,23 | 0,16 | 0,13 | 0,11 | 0,10 | 0,09 | 0,09 | 0,09 |
| 24 | 1.09 | 0,44 | 0,25 | 0,17 | 0,14 | 0,11 | 0,10 | 0,10 | 0,10 | 0,10 |
Atualmente, a precisão do eixo Y das dobradeiras geralmente pode atingir 0,01 mm, portanto o desvio do ângulo não deve ser muito severo. Mas será que a espessura da chapa metálica pode ser garantida como perfeitamente consistente?
Se uma chapa de 1,5 mm de espessura varia em 10% na espessura, isso representa uma diferença de 0,15 mm, equivalente a uma diferença de 0,15 mm na distância entre as matrizes superior e inferior, resultando em um desvio angular de aproximadamente 3°.
Da mesma forma, uma variação de 10% nas características de endurecimento por deformação da chapa metálica pode causar uma mudança de cerca de 1,5° no ângulo de flexão. O impacto da espessura da chapa metálica e do endurecimento por deformação no ângulo de flexão durante a flexão a ar é mostrado na Figura 6.
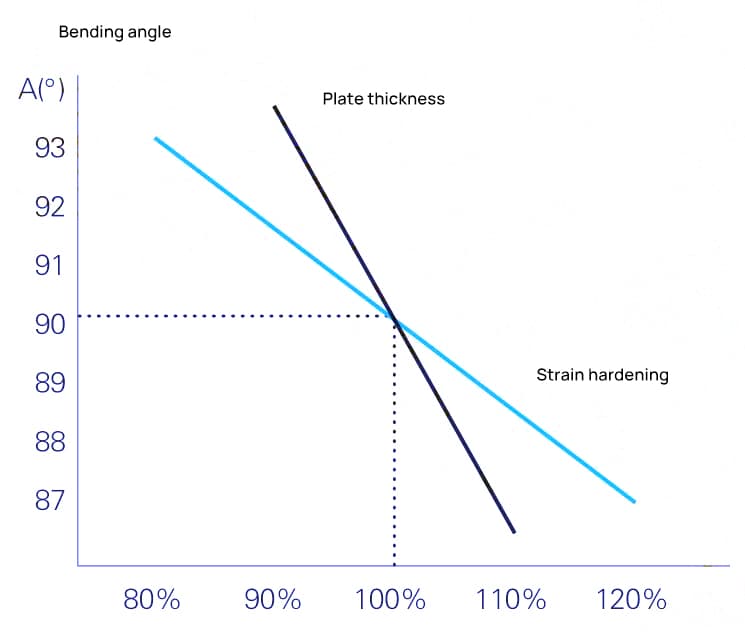
É aqui que as máquinas de dobra diferem das máquinas-ferramentas de corte de metal. Com máquinas de corte de metal, independentemente das diferenças de tamanho entre as peças brutas, a precisão final das peças usinadas pode ser garantida desde que a máquina-ferramenta seja suficientemente precisa.
No entanto, este não é o caso da prática comum de flexão de ar em dobradeiras; não é uma questão de precisão inerente à máquina.