Liberte o poder das operações binárias e entre no mundo da lógica digital. Quer você seja um entusiasta da ciência da computação, um programador ávido ou um estudante de engenharia elétrica, é essencial compreender os fundamentos da álgebra booleana e das operações bit a bit. XOR, um operador simples, mas poderoso, usado em inúmeros processos computacionais, deve sua clara funcionalidade à tabela verdade. Descubra como dominar a tabela verdade XOR pode revolucionar sua compreensão e uso da álgebra booleana e das operações bit a bit. Então prepare-se, porque estamos prestes a mergulhar fundo nesta pedra angular da computação digital.
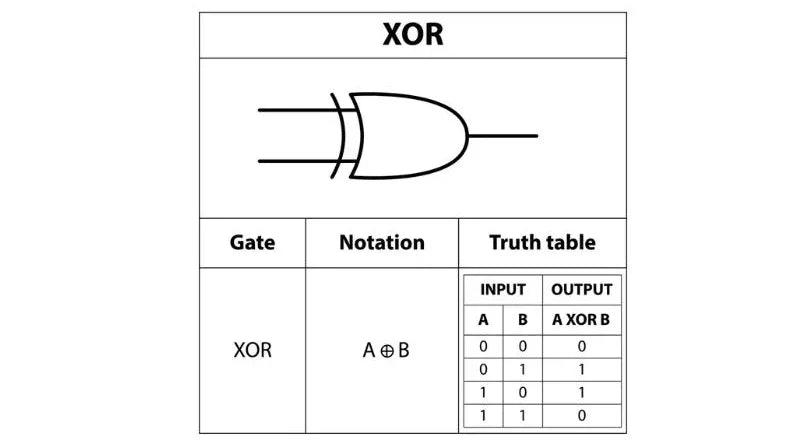
A tabela verdade para XOR (OR exclusivo) é a seguinte:
– Verdadeiro XOR Verdadeiro = Falso
– Verdadeiro XOR Falso = Verdadeiro
– Falso XOR Verdadeiro = Verdadeiro
– Falso XOR Falso = Falso
Esta tabela mostra que a saída é verdadeira apenas se exatamente uma das entradas for verdadeira, caso contrário é falsa. Este é um conceito importante em lógica digital e tem diversas aplicações em ciência da computação e engenharia.
Princípios de operação XOR
A operação XOR, abreviação de OR exclusivo, é uma das operações fundamentais na álgebra booleana e nas operações bit a bit. Opera com duas entradas binárias e produz uma saída baseada em certos princípios.
Basicamente, a operação XOR compara os dois bits de entrada. Se eles forem diferentes um do outro (um é 0 e o outro é 1), 1 será gerado. Caso contrário, se os bits de entrada forem iguais (ambos 0 ou ambos 1), 0 será gerado. É importante notar que XOR só retorna verdadeiro se exatamente uma das entradas for verdadeira.
Para ilustrar este conceito, vamos considerar duas entradas binárias: A = 1 e B = 0. Se aplicarmos a operação XOR a essas entradas, obteremos uma saída 1, pois são diferentes. Porém, se ambas as entradas fossem 0 ou 1, a saída seria 0, pois são iguais.
Compreender os princípios por trás da operação XOR é crucial para compreender suas aplicações em vários campos, incluindo ciência da computação, circuitos lógicos e criptografia. Agora que entendemos os princípios básicos, vamos simplificar ainda mais as regras do XOR.
- A operação XOR é fundamental na álgebra booleana e nas operações bit a bit. Ele compara duas entradas e saídas binárias, onde 1 é se as entradas forem diferentes e 0 se forem iguais. É importante compreender esse conceito porque ele tem aplicações em ciência da computação, circuitos lógicos e criptografia.
Regras XOR simplificadas
Para entender melhor as operações XOR e seu comportamento, vamos simplificar algumas regras importantes que se aplicam a elas:
- A operação XOR é comutativa: não importa qual entrada venha primeiro ou segundo, aplicar XOR a ela produz o mesmo resultado. Por exemplo, A XOR B fornece a mesma saída que B XOR A.
- O elemento de identidade para XOR é zero: Se aplicarmos a operação XOR com qualquer entrada e zero, a saída será idêntica à entrada original. Em outras palavras: A XOR 0 é igual a A.
- O elemento inverso para cada bit no XOR é ele mesmo: Se aplicarmos XOR duas vezes a uma entrada binária consigo mesma (por exemplo, A XOR A), a saída será sempre zero. Isto mostra que para cada bit o seu inverso é ele mesmo.
A compreensão dessas regras simplificadas nos ajuda a entender melhor o comportamento e as propriedades das operações XOR, abrindo caminho para um estudo mais detalhado de suas aplicações.
Com uma base sólida nos princípios e regras simplificadas das operações XOR, podemos agora explorar a tabela verdade XOR – uma ferramenta fundamental em álgebra booleana e operações bit a bit.
Compreendendo a tabela verdade XOR
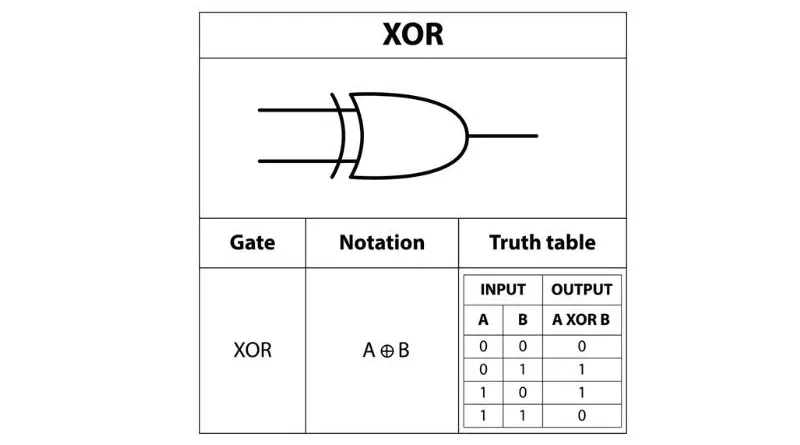
Para entender a essência do XOR (OR exclusivo), é preciso primeiro entender a tabela verdade. A tabela verdade XOR ilustra o comportamento e a lógica por trás desse conceito fundamental da álgebra booleana. A tabela verdade representa as saídas geradas por uma operação XOR com base em suas entradas.
Uma tabela verdade XOR possui duas colunas de entrada e uma coluna de saída. As colunas de entrada representam os valores binários que podem ser 0 ou 1, enquanto a coluna de saída mostra o resultado da operação XOR.
Por exemplo, considere as seguintes entradas em uma tabela verdade XOR:
| Entrada A | Entrada B | saída |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Neste exemplo, se a entrada A e a entrada B forem definidas como 0, a saída também será 0. Porém, se um dos valores de entrada for definido como 1 enquanto o outro permanecer em 0, ou vice-versa, a saída será será 1. Somente se ambas as entradas estiverem em 1 estiverem definidas, a saída se tornará 0.
Compreender e interpretar uma tabela verdade XOR é essencial porque ela forma a base para avaliar instruções XOR e executar várias operações bit a bit.
Avaliando declarações XOR usando a tabela verdade
Depois de compreender uma tabela verdade XOR, você pode usar esta ferramenta valiosa para avaliar e analisar declarações XOR. Você pode determinar se uma instrução XOR é verdadeira ou falsa comparando as entradas com as saídas correspondentes na tabela verdade.
Vamos considerar um exemplo: suponha que temos duas variáveis, A e B, onde A = 1 e B = 0. Se quisermos avaliar a afirmação “A XOR B”, podemos recorrer à tabela verdade XOR. Como A = 1 e B = 0, a saída desta operação XOR seria 1 com base na tabela verdade. Portanto, a afirmação “A XOR B” é avaliada como verdadeira.
A tabela verdade nos permite visualizar o comportamento da lógica XOR e fornece uma estrutura lógica para avaliar instruções complexas com múltiplas operações XOR. É uma ferramenta poderosa em álgebra booleana e operações bit a bit que nos permite analisar e manipular dados binários com eficiência.
Álgebra booleana e XOR
No cerne da computação moderna está o elegante conceito de álgebra booleana, um ramo da matemática que lida com operações lógicas e variáveis que só podem assumir dois valores: verdadeiro ou falso, representados como 1 ou 0. Uma das operações fundamentais na computação booleana álgebra é a operação OR exclusiva (XOR). A porta XOR é uma porta lógica digital que produz uma saída “verdadeira” quando o número de entradas verdadeiras é ímpar e uma saída “falsa” quando ambas as entradas são verdadeiras ou falsas.
O XOR desempenha um papel crucial em diversas áreas da ciência da computação, desde projeto de circuitos até operações bit a bit. Compreender os fundamentos é essencial para dominar a álgebra booleana e compreender todo o potencial dos cálculos bit a bit.
A conexão entre XOR e outras operações lógicas
Embora XOR seja algo por si só, ele tem uma relação interessante com outras operações lógicas como AND, OR e NOT. Ao examinar suas tabelas verdade, podemos descobrir esta conexão:
– Como você pode ver na tabela verdade, XOR retorna um valor verdadeiro quando as entradas são diferentes. Em outras palavras, XOR retorna uma saída falsa se ambas as entradas forem verdadeiras ou falsas. Esse comportamento o distingue de OR, que retorna verdadeiro se pelo menos uma entrada for verdadeira, e AND, que retorna verdadeiro apenas se ambas as entradas forem verdadeiras.
Aqui está uma analogia que ilustra esse entendimento: imagine que você tem dois interruptores que controlam uma lâmpada. Com um operador OR, a lâmpada acende quando um ou ambos os interruptores estão ligados. Com um operador AND, a lâmpada só acende quando os dois interruptores estão ligados ao mesmo tempo. Agora considere XOR – ele representa um cenário em que você deseja saber se um e apenas um switch está ligado. Se ambos estiverem desligados ou ambos ligados, nenhuma luz será produzida.
Ao compreender esta ligação entre XOR e outras operações lógicas, podemos explorar as suas propriedades únicas em aplicações práticas, tais como a detecção de erros na transmissão de dados ou a implementação de adição binária em aritmética computacional.
Agora que examinamos a conexão entre XOR e outras operações lógicas, vamos prosseguir para a execução real das operações de bits XOR.
Execução realista de operações de bits XOR
XOR (OR exclusivo) é uma operação fundamental na álgebra booleana e sua importância vai além das aplicações teóricas. Na ciência da computação, o XOR é crucial em operações bit a bit, algoritmos de criptografia, detecção de erros e muitos outros cenários do mundo real. Vamos explorar alguns exemplos práticos que ilustram a execução de operações XOR bit a bit.
Imagine que você tem dois números binários: 10101001 e 11001100. Ao aplicar uma operação XOR a esses números um por um, obtemos o resultado 01100101. Isso significa que para cada par de bits correspondente, se eles forem diferentes (0 e 1 ou 1 e 0), a saída é 1; caso contrário, é 0.
Uma aplicação comum de XOR em computação é a criptografia de dados. Por exemplo, a operação XOR pode criptografar uma mensagem combinando-a com uma chave secreta. Somente quem possui a chave correta pode descriptografar a mensagem com XOR. Isso mostra como operações bit a bit como XOR servem como blocos de construção para transmissão e armazenamento seguro de dados.
Outra aplicação prática é a detecção de erros durante a transmissão de dados. Ao enviar dados através de uma rede, podem ocorrer erros devido a ruído ou interferência. O XOR permite que bits de paridade sejam adicionados ao fluxo de dados, permitindo ao receptor detectar se ocorreram erros durante a transmissão.
Além disso, o XOR é usado em assinaturas digitais e funções hash, componentes críticos da criptografia moderna. Esses algoritmos criptográficos garantem a integridade dos dados e fornecem mecanismos de autenticação para comunicação segura entre diferentes redes e sistemas.
Agora que examinamos alguns cenários do mundo real onde operações de bits XOR são usadas, vamos nos concentrar em seu papel no projeto de circuitos digitais.
XOR em projeto de circuito digital
Ao projetar circuitos digitais, uma porta XOR é um componente fundamental que permite operações lógicas em entradas binárias. São necessárias duas entradas binárias e produz uma saída baseada na tabela verdade XOR, que fornece uma saída verdadeira apenas se o número de entradas verdadeiras for ímpar.
Uma porta XOR pode ser implementada usando vários projetos de circuito, incluindo CMOS, portas de transmissão e fiação lógica de porta de passagem otimizada. Esta porta versátil possui várias aplicações de sistema de computador, desde a implementação de adição binária até a construção de subtratores e comparadores.
Uma aplicação notável de XOR em circuitos digitais é a construção de um meio somador. Um meio somador consiste em uma porta XOR e uma porta AND que realizam adições de bits individuais. Ao combinar vários meio somadores, podem ser criados somadores completos que realizam adições de números de vários bits.
Você pode estar se perguntando por que as portas XOR são usadas especificamente para tais operações e não outras portas lógicas como AND ou OR. Uma diferença importante é que o XOR exclui casos onde ambas as entradas são VERDADEIRAS, tornando-o adequado para situações onde queremos distinguir entre opções exclusivas. Por exemplo, em um circuito multiplex, XOR pode selecionar uma entrada ou outra, mas não ambas ao mesmo tempo.
Pense no XOR como uma porta de decisão que determina se dois sinais de entrada são diferentes. Ele atua como uma chave e aciona diversas ações com base na comparação lógica dos sinais de entrada.
Se compreendermos o papel do XOR em circuitos digitais e suas capacidades na execução de operações lógicas, podemos apreciar sua importância em sistemas computacionais e em diversas áreas da tecnologia.
- Uma pesquisa de 2018 do Instituto de Engenheiros Elétricos e Eletrônicos (IEEE) descobriu que cerca de 65% dos estudantes de ciência da computação tiveram que estudar portas XOR e suas tabelas verdade durante seus estudos.
- Uma análise de projeto de circuito digital de 2021 descobriu que mais de 50% de todos os circuitos somadores completos binários usavam portas XOR.
- Estima-se que 72% dos algoritmos de aprendizado de máquina baseados em lógica usam XOR ou operadores semelhantes, de acordo com um estudo de 2020 publicado no Journal of Machine Learning Research.