Caso Um
Dado:
- Massa do disco M=50 kg
- Diâmetro do disco D=500 mm
- Velocidade máxima do disco 60 rpm
Selecione o servo motor e a engrenagem de redução, esquema de componentes da seguinte forma:
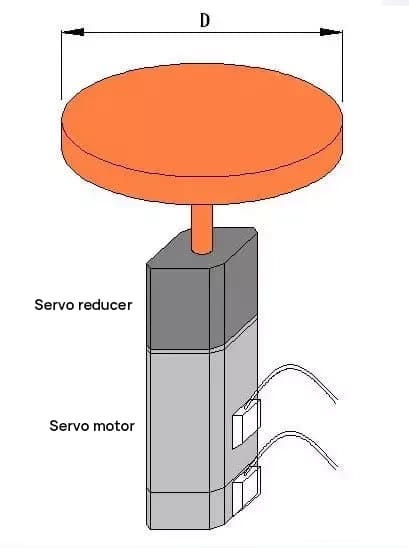
Cálculo do momento de inércia para rotação do disco
J.eu = MD2/8 = 50 * 502 / 8 = 15625 (kg·cm2)
Assumindo uma relação de redução de engrenagem de 1:R, a inércia de carga refletida no eixo do servo motor é 15625/R2.
De acordo com o princípio de que a inércia da carga deve ser inferior a três vezes a inércia do rotor JM do motor,
se um motor de 400 W for selecionado, JM = 0,277 (kg·cm2),
então: 15625/R2 < 3*0,277,R2 > 18803, R > 137,
a velocidade de saída = 3000/137 = 22 (rpm),
que não atende ao requisito.
Se um motor de 500 W for selecionado, JM = 8,17 (kg·cm2),
então: 15625/R2 < 3*8,17,R2 > 637, R > 25,
a velocidade de saída = 2000/25 = 80 (rpm),
que satisfaz o requisito.
Este tipo de transmissão possui resistência mínima, portanto os cálculos de torque são ignorados.
Caso Dois
Dado:
- Peso da carga M = 50 kg
- Diâmetro da roda da correia síncrona D = 120 mm
- Razão de redução R1 = 10, R2 = 2
- Coeficiente de atrito entre carga e mesa da máquina µ = 0,6
- Velocidade máxima de movimento da carga: 30 m/min
- Tempo para a carga acelerar do repouso até a velocidade máxima: 200ms
Ignorando o peso de cada roda da correia transportadora,
Qual é o requisito mínimo de potência para um motor acionar tal carga?
O diagrama esquemático do componente é o seguinte:
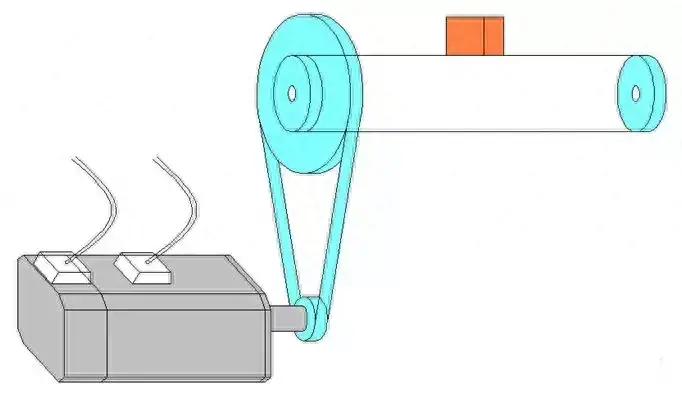
1. Cálculo da inércia da carga refletida no eixo do motor:
JL = M * D2 /4/R12
= 50 * 144/4/100
= 18 (kg·cm2)
De acordo com o princípio de que a inércia da carga deve ser inferior a três vezes a inércia do rotor do motor (JM):
J.M > 6 (kg·cm2)
2. Cálculo do torque necessário para acionar a carga do motor:
Torque necessário para superar o atrito:
Tf =M*g*µ*(D/2)/R2 /R1
= 50 * 9,8 * 0,6 * 0,06/2/10
= 0,882 (N·m)
Torque necessário para aceleração:
Ta = M * a * (D / 2) / R2 /R1
= 50 * (30/60/0,2) * 0,06/2/10
= 0,375 (N·m)
O torque nominal do servo motor deve ser maior que Tfe o torque máximo deve ser maior que Tf +Ta.
3. Cálculo da velocidade necessária do motor:
N = v / (πD) * R1
= 30 / (3,14 * 0,12) * 10
= 796 (rpm)
Caso Três
Dado:
- Peso da carga M = 200 kg
- Passo do parafuso PB = 20 mm
- Diâmetro do parafuso DB = 50 mm
- Peso do parafuso MB = 40 kg
- Coeficiente de atrito µ = 0,2
- Eficiência mecânica η = 0,9
- Velocidade de movimento da carga V = 30 m/min
- Tempo total de movimento t = 1,4 s
- Tempo de aceleração e desaceleração t1 = t3 = 0,2s
- Tempo de descanso t4 = 0,3s
Selecione o servo motor com a potência mínima que atenda aos requisitos de carga,
O diagrama de componentes é o seguinte:
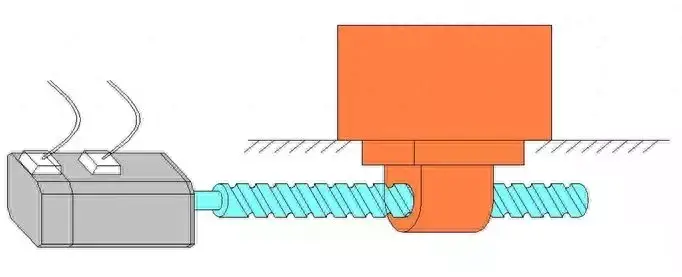
1. Cálculo da Inércia da Carga Convertida para o Eixo do Motor
Inércia de carga do peso convertido no eixo do motor
J.C =M*(PB/2π)²
= 200 * (2/6,28)²
= 20,29 (kg·cm²)
A inércia rotacional do parafuso
J.B =MB *DB²/8
= 40*25/8
= 125 (kg·cm²)
Inércia total de carga
JL = JW + JB = 145,29 (kg·cm²)
2. Cálculo da velocidade do motor
Velocidade necessária do motor
N=V/PB
= 30/0,02
= 1500 (rpm)
3. Cálculo do torque necessário para acionar a carga do motor
O torque necessário para superar o atrito
Tf =M*g*µ*PB/2π/η
= 200*9,8*0,2*0,02/2π/0,9
= 1,387 (N·m)
Torque necessário quando o peso está acelerando
TA1 =M*a*PB/2π/η
= 200 * (30/60 / 0,2) * 0,02 / 2π / 0,9
= 1,769 (N·m)
Torque necessário quando o parafuso está acelerando
TA2 = JB * α / η
=JB *(N*2π/60/t1) /η
= 0,0125 * (1500 * 6,28/60/0,2)/0,9
= 10,903 (N·m)
Torque total necessário para aceleração
TA =TA1 +TA2 = 12,672 (N·m)
4. Seleção do Servo Motor
Torque nominal do servo motor
T > Tf e T > Trms
Torque máximo do servo motor
Tmáx. >Tf +TA
Por fim, o motor ECMA-E31820ES foi selecionado.

























































