1. Teoria da tensão máxima de tração (a primeira teoria de resistência é a tensão principal máxima):
Esta teoria é comumente referida como a primeira teoria da força. Afirma que a principal causa da falha é a tensão máxima de tração. Se a primeira tensão principal atingir o limite de resistência à tração uniaxial, independentemente da complexidade ou simplicidade do estado de tensão, isso resultará em fratura.
Formulário de falha: Fratura
Condições de dano: σ1 =σb
Condição de resistência: σ1≤(σ)
Experimentos mostraram que esta teoria de resistência pode explicar melhor o fenômeno de fratura de materiais frágeis como pedra e ferro fundido, particularmente em áreas onde está localizada a tensão máxima de tração. No entanto, não é adequado para casos sem tensão de tração, como compressão unidirecional ou compressão tripartida.
Desvantagem: Não considera as outras duas tensões principais.
Âmbito de aplicação: Esta teoria é adequada para a tensão de materiais frágeis, como alongamento e torção de ferro fundido.
2. Teoria da deformação linear de alongamento máximo (a segunda teoria de resistência é a deformação principal máxima)
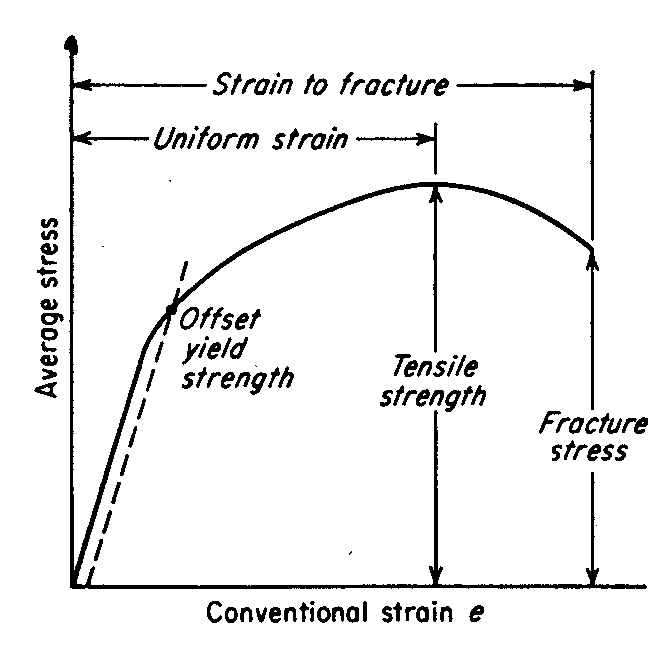
Esta teoria é comumente referida como a segunda teoria da força. Ele postula que a principal causa da falha é a deformação linear máxima de alongamento. Se a primeira deformação principal atingir o valor limite da tensão uniaxial, independentemente da complexidade ou simplicidade do estado de tensão, resulta em fratura.
Suposição de falha: A deformação máxima de alongamento atinge o limite da tensão simples (assumindo que a lei de Hooke ainda pode ser usada para calcular até que ocorra a fratura).
Formulário de falha: Fratura
Condições de fratura frágil: ε1 = εu = σb/E;
ε1 = 1/E (σ1−μ(σ2+σ3));
Condições de dano: σ1−μ(σ2+σ3) = σb;
Condição de resistência: σ1−μ(σ2+σ3)≤(σ)
Experimentos mostraram que esta teoria de resistência pode explicar melhor o fenômeno de fratura de materiais frágeis, como pedra e concreto, sob tensão axial. No entanto, tem sido raramente utilizado porque os seus resultados experimentais são consistentes apenas com alguns materiais e não podem explicar amplamente a lei geral da falha por fratura frágil.
Desvantagem: Não explica a lei geral da falha por fratura frágil.
Âmbito de aplicação: Esta teoria é adequada para a compressão axial de pedra e concreto.
3. Teoria da tensão máxima de cisalhamento (a terceira teoria de resistência, nomeadamente resistência Tresca):
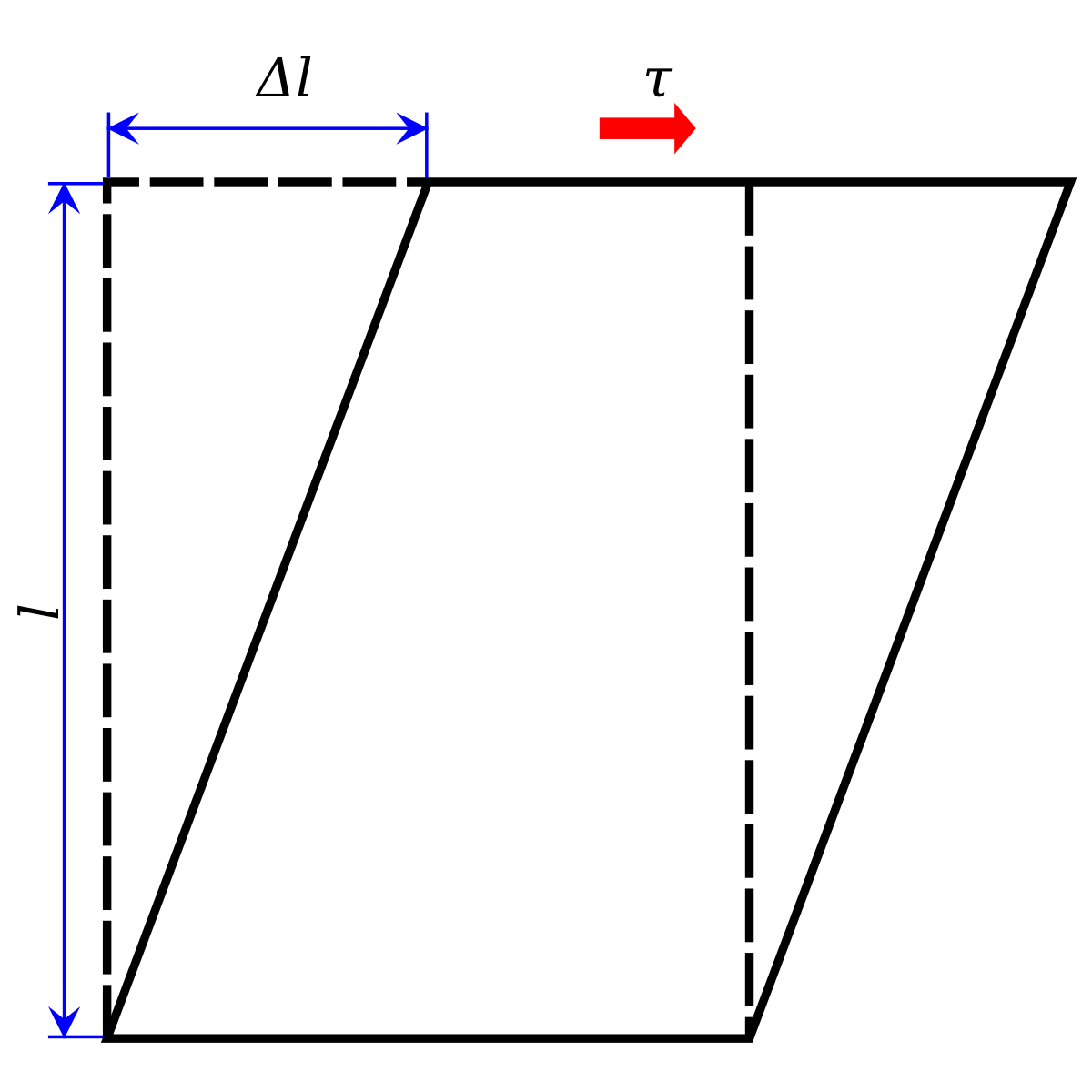
Esta teoria, conhecida como terceira teoria da resistência, postula que a principal causa da falha é a tensão de cisalhamento máxima (τmax). A teoria afirma que, independentemente da complexidade ou simplicidade do estado de tensão, uma vez que a tensão de cisalhamento máxima atinja o valor final da tensão de cisalhamento sob tensão uniaxial, ocorrerá o escoamento.
A suposição de falha é que quando a tensão de cisalhamento máxima em um estado de tensão complexa atinge o limite de tensão de cisalhamento do material durante tração e compressão simples, a falha ocorrerá na forma de escoamento. O principal fator que contribui para a falha é a tensão de cisalhamento máxima, que é igual à tensão de cisalhamento última (τmax=τu=σs/2).
A condição de falha de rendimento é definida como τmax=1/2(σ1−σ3), e as condições de dano são atendidas quando σ1−σ3=σs. A condição de resistência é declarada como σ1−σ3≤(σ).
Experimentos mostraram que esta teoria fornece uma explicação melhor para a deformação plástica de materiais plásticos. No entanto, deve-se notar que esta teoria não leva em consideração a influência de 2σ e, como resultado, os componentes projetados com base nesta teoria tendem a ser excessivamente conservadores.
Desvantagens: nenhuma influência 2 σ
Âmbito de aplicação: adequado para condições gerais de materiais plásticos.
A forma é simples, o conceito é claro e o maquinário é amplamente utilizado.
Mas o resultado teórico é mais seguro que o real.
4. Teoria da energia específica da mudança de forma (quarta teoria da força, nomeadamente força de von mises)
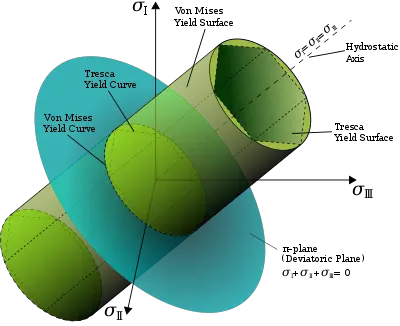
Esta teoria é referida como a quarta teoria da resistência e postula que a razão para o escoamento de um material é a energia específica (DU) da mudança de forma atingindo um determinado valor limite, independentemente do estado de tensão.
As condições de dano são definidas como 1/2(σ1−σ2)2+2(σ2−σ3)2+(σ3−σ1)2=σs, e a condição de resistência é dada como σr4= 1/2(σ1−σ2) 2+ (σ2−σ3)2 + (σ3−σ1)2≤(σ).
Dados experimentais de testes de tubos finos em diversos materiais (aço, cobre, alumínio) mostraram que a teoria da energia específica da mudança de forma está mais alinhada com os resultados experimentais em comparação com a terceira teoria de resistência.
Uma forma unificada das quatro teorias de resistência pode ser estabelecida tendo uma tensão equivalente (σrn) que possui uma expressão unificada da condição de resistência (σrn≤(σ)). A tensão equivalente pode ser expressa da seguinte forma:
σr1=σ 1≤(σ)
σr2=σ1−μ(σ2+σ3)≤(σ)
σr3=σ1−σ3≤ (σ)
σr4= 1/2(σ1−σ2)2+(σ2−σ3)2+(σ3−σ1)2≤ (σ)
5. Teoria da força de Mohr
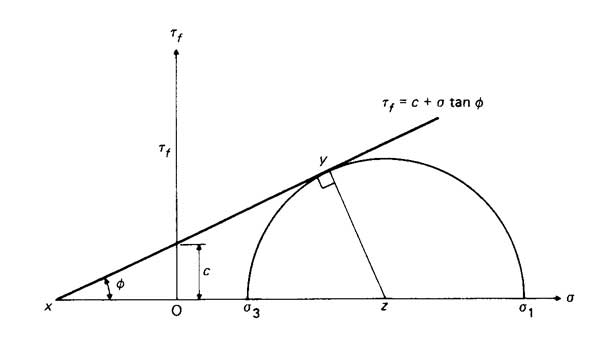
A teoria da resistência de Mohr não se baseia na suposição de que a falha nos materiais é causada por um único fator (como tensão, deformação ou energia específica) atingindo seu valor limite. Em vez disso, é uma teoria de resistência baseada nos resultados de testes de falha de materiais sob vários estados de tensão.
Esta teoria considera as diferenças entre as resistências à tração e à compressão dos materiais, reconhece a tensão de cisalhamento máxima como a principal causa do escoamento e leva em consideração a influência da tensão normal no plano de cisalhamento.
Embora a teoria da resistência de Mohr reconheça as diferentes capacidades de tração e compressão dos materiais, o que é consistente com materiais frágeis (como rocha e concreto), ela não leva em conta a influência da tensão principal intermediária 2a, o que é uma limitação da teoria.
6. Âmbito de aplicação da teoria da resistência
A resistência de um material não é determinada apenas pela natureza do material, mas também pelo estado de tensão no ponto de falha.
Os materiais frágeis são normalmente analisados usando a teoria da resistência da fratura frágil ou a teoria da resistência de Mohr, enquanto os materiais plásticos são analisados usando a teoria da resistência ao escoamento.
No entanto, o modo de falha nos materiais também está relacionado ao estado de tensão. Por exemplo, sob a condição de tensão de tração tridimensional, seja um material plástico ou frágil, ele falhará na forma de fratura, e a teoria da tensão de tração máxima deve ser usada. No caso de tensão de compressão tridimensional, ocorre deformação plástica, e a terceira ou quarta teoria de resistência deve ser usada.