A viga da ponte é geralmente construída como uma viga protendida ou protendida. Além de vigas pré-fabricadas, também são construídas lajes de concreto sobre encontros, bueiros em caixão, vigas em caixão e pontes suspensas, aquelas para tráfego de passageiros ou veículos.
O projeto da viga da ponte de concreto protendido discutido neste artigo está em conformidade com a BS 8110 Parte 1.
Neste artigo discutimos o Projeto ULS (estimativa ULS da capacidade de momento fletor) uma viga de ponte protendida com Método de compatibilidade de deformação.
Vamos discutir um pouco sobre o método de compatibilidade root.


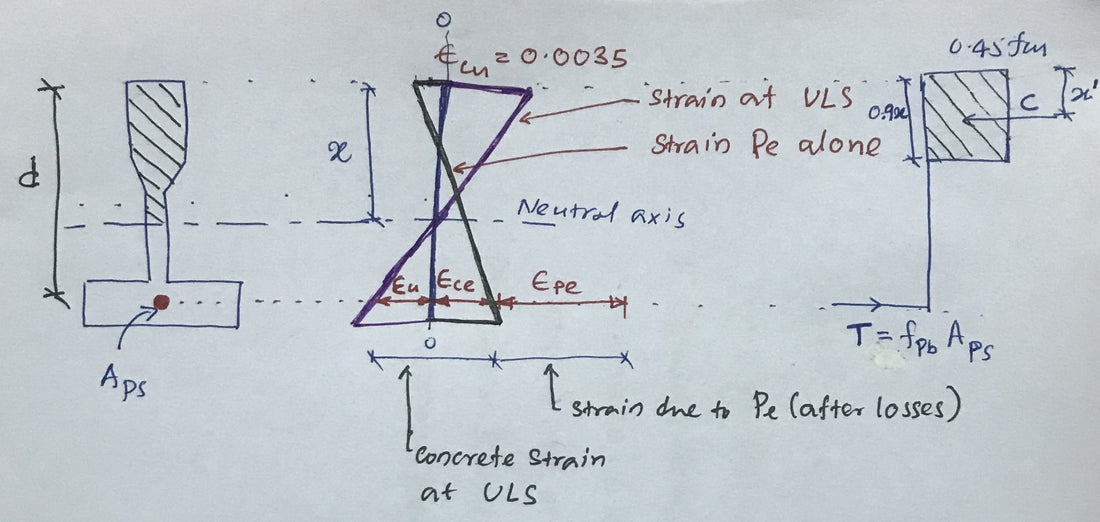
Deformação no estado limite último (εpb )Ao selecionar superfícies de tensão, preste atenção aos seguintes componentes.
- Alongamento devido à força de tração efetiva (Pe) (após perdas) – εEsportes
- Deformação causada pela carga aplicada – εPai
O alongamento devido à pré-carga Pe é calculado da seguinte forma
εEsportes =Pt / (Aobs:.Eobs: )
Onde Aobs: é a área dos tendões e Eobs: é o módulo de elasticidade do aço.
Durante a protensão, a compressão está abaixo do eixo neutro e a seção está sujeita a tensões de compressão εce E εEsportes.
Aqui, εceé a tensão de compressão na seção no plano do aço através do “Esportes“.
A carga aplicada inicialmente causa esta expansão (εce) zero, e então a tensão de tração do aço é desenvolvida. A tensão de tração total desenvolvida pela carga no estado limite último é
εPai = εce + εEla
Avançar,
Redução da tensão de compressão do concreto = aumento da tensão de tração do aço
Isso ocorre porque o aço e o concreto estão na mesma seção. A tensão do concreto diminui e ao mesmo tempo a tensão do aço aumenta. Ambos acontecem ao mesmo tempo.
Aqui,
εce =fcom / EC = (Pt/EC) ( 1/A + e2/EU)
εEla = εcu (d – x) / x = 0,0035 (d – x) /x
A tensão de tração do aço pode ser expressa como
εpb = εEla + εce + εEsportes
Precisamos usar um processo iterativo para calcular a profundidade do eixo neutro até que a força de impulso seja igual à força de tração (C = T).
Depois de calcularmos a deformação de tração (εpb ), calcule a capacidade de flexão da seção usando a seguinte equação.
MEla =fpb Aobs: (t')
Ao calcular a capacidade de flexão da viga da ponte, são executados os seguintes passos.
- Suponha uma profundidade natural do eixo e calcule a força de compressão (C = 0,45 fcu A'C)
- Em seguida, calcule a tensão de tração no tendão.
- Para fazer isso, calcule as tensões de tração nos tendões (εpb = εEla + εce + εEsportes)
- E então você encontra o strass de aço na curva tensão-deformação
- Verifique se a força de tração (T=fpb Aobs:) e a força de compressão é a mesma.
- Caso contrário, repita o cálculo alterando as profundidades do eixo neutro até que sejam iguais.
- Após determinar a profundidade do eixo neutro, calcule a capacidade de flexão da seção (MEla =fpb Aobs: (dd')).
Vamos explorar isso com um exemplo prático
Dados para projeto de vigas de ponte
- Envergadura = 16m
- Peso da laje = 1 kN/m
- Carga útil = 4 kN/m
- Densidade do concreto 24 kN/m3
- Resistência ao escoamento dos tendões, fpu = 1670 N/mm2
- Área dos tendões, Aobs: = 882mm2
- Resistência do cubo de concreto, fcu = 40 N/mm2
- Área da seção transversal, A = 121.000 mm2
- Módulo de elasticidade do aço, Eobs: = 205kN/mm2
- Módulo de elasticidade do concreto, Ecu = 28 N/mm2
- Momento de inércia da área da seção transversal, I = 5,236×109 milímetros4
- Força de pré-carga, Pt = 744 kN


Calcular o torque nominal
Os fatores de carga de projeto foram adotados da BS 8110.
Área da seção = 121.000 mm2
Peso próprio da viga = 121.000 x 10-6 x 24 = 2,9 kN/m
Carga de projeto = 1,4 (2,9 + 1) + 1,6 x 4 = 11,86 kN/m
Torque nominal = wl2/8 = 11,86 x 162 / 8 = 379,52 kN·m
Teste de resistência ao momento
Calcule a profundidade do eixo neutro
Suponha o eixo neutro, x = 400 mm da fibra mais externa superior
Altura do bloco de tensão compressiva = 0,9 x = 0,9 x 400 = 360mm


Área do bloco de tensão compressiva, A'C = LIGADO1 + UM2 + UM3
A'C = 150×200 + 0,5x(200+100)x75 + 135×100 = 54,75×103 milímetros2
Força compressiva
C = 0,45.fcu.A'C
C = 0,45 x 40 x 54,75 x 103 = 985,5 × 103 N = 985,5 kN
Calcular a força de tração
T=fpb Aobs:
Primeiro temos que calcular a tensão de tração (fpb). Vamos usar tensão nesta seção.
εpb = εEsportes + εce + εEla = Pt/(Aobs:.Eobs:) + (Pt/EC)(1/A + t2/EU) + 0,0035(dx)/x
εEsportes =Pt/(Aobs:.Eobs:) = 744×103 / (882×205×103) = 4,11 x 10-3
εce = (Pt/EC)(1/A + t2/eu = (744×103/28×103)(1/121000 + 1992/5.236×109) = 0,42 x 10-3
εEla = 0,0035(dx)/x = 0,0035x ((199+364) -400) / 400 = 1,43 x 10-3
εpb = 4,11 x 10-3 +0,42×10-3 + 1,43×10-3 = 5,96×10-3
O alongamento do tendão é 5,96 x 10-3 ≈ 0,006
A partir do diagrama de tensão e deformação para cabos na BS 8110 Parte 01, as seguintes informações podem ser levadas em consideração para o projeto


As seguintes informações estão disponíveis
- ϒM = 1,5
- Fpu = 1670 N/mm2
- Eobs: = 205kN/mm2
Fpu/γM = 1670 / 1,15 = 1452,2 N/mm2
0,8fpu/γM = 1452,2 x 0,8 = 1161,7 N/mm2
Fpu/γMEobs: = 1670 / (1,15 x 205×103) = 0,0071
0,8fpu/γMEobs: = 0,0071 x 0,8 = 0,0057
Agora os valores na imagem acima podem ser marcados da seguinte forma.


Através da interpolação linear podemos determinar a tensão nos tendões.
Fpb = 1175,3 N/mm2
área do tendão, Aobs: = 882 mm2
Agora podemos calcular a força de tração,
T=fpb Aobs: = 1175,3 x 882 = 1036,6×103 N = 1.036,6 kN
C = 985,5 kN
T ≠ C, a profundidade do eixo neutro assumida está incorreta. Temos que repetir o mesmo procedimento até T = C.
Podemos precisar fazer várias iterações para chegar perto da profundidade correta do eixo neutro.
Primeiro verificamos a faixa da profundidade do eixo neutro.
Podemos assumir C = 1036,6 kN (força de tração) e então verificar a profundidade
C = 0,45.fcu.A'C
1036,6×103 = 0,45x40x A'C
A'C = 57588,9 mm2
57588,9 = 150×200 + 0,5x(200+100)x75 + (0,9x – 150 – 75 )x100
x = 431,54 mm
Portanto podemos dizer que “x” deve ser menor que este valor.
Suponha que x = 425 mm
εpb = 4,11 x 10-3 +0,42×10-3 + 0,0035x ((199+364) -425) / 425 = 0,0057
Siga o mesmo procedimento da tabela acima.
Fpb = 1161,7 N/mm2
T =fpb Aobs: = 1161,7 x 882 = 1024,6×103 N = 1.024,6 kN
C = 0,45.fcu.A'C = 0,45 x 40 x (150×200 + 0,5x(200+100)x75 + 157,5×100} = 1026×103 N = 1.026 kN
Portanto podemos concluir que T ≈ C
Então, para calcular a capacidade de flexão, considere x = 425 mm.
MEla =fpb Aobs: (t')
Onde d' é o centro de gravidade do bloco de tensão compressiva.


d' pode ser calculado calculando o momento em torno de uma aresta. Então o cálculo não é levado em consideração porque é um cálculo simples.
d' = 159,6 mm
Vamos calcular a capacidade de flexão.
MEla =fpb Aobs: (t')
Esta equação pode ser escrita da seguinte forma:
MEla = T (d – d')
MEla= 1024,6 (563 -159,6)/1000 = 413,3 kN·m
A capacidade de flexão é de 413,3 kNm e o momento de flexão aplicado é de 379,52 kNm. A seção é adequada para dobrar.
No entanto, a seção deve ser testada quanto ao cisalhamento. Informações sobre dimensionamento de vigas de concreto protendido podem ser encontradas em um artigo separado.
O artigo Construção de ponte de acordo com BS 5400 poderia ser consultado para fornecer mais informações sobre a teoria do projeto de vigas de pontes.
Leitura adicional sobre peças pré-moldadas de concreto: artigo da Wikipedia concreto protendido poderia ser encaminhado.