No tutorial anterior, foram discutidas várias portas lógicas e sua construção. No tutorial – Operações Lógicas Booleanas, foi discutido como, ao realizar operações lógicas em dados binários, operações aritméticas podem ser executadas. Em um circuito digital, muitas portas lógicas são interconectadas juntamente com registros e elementos de memória para realizar uma tarefa computacional complexa. Qualquer problema computacional pode ser expresso como uma função booleana ou expressão booleana.
Uma expressão booleana leva em consideração as variáveis booleanas (que podem ser vistas como fontes de dados binários individuais) e representar relação matemática (na forma de adição e multiplicação) entre eles. As operações matemáticas como divisão e subtração são executadas pela própria multiplicação e adição. Da mesma forma, a subtração pode ser implementada por adição com o complemento e a divisão pode ser implementada pela multiplicação do divisor por um fator e subtração.
As funções ou expressões booleanas seguem um conjunto de regras matemáticas que são chamadas coletivamente de álgebra booleana. Os vários teoremas da álgebra booleana são úteis para minimizar uma função booleana. Para projetar um circuito digital otimizado (número mínimo de portas lógicas para resolver um problema computacional específico), uma expressão booleana deve ser minimizada. Então, vamos começar com teoremas e postulados básicos da álgebra booleana.
Postulados de Huntington –
A Álgebra Booleana foi desenvolvida por George Boole no ano de 1854. Em 1904, EV Huntington formulou vários postulados que devem ser satisfeitos por um sistema algébrico booleano. Esses postulados são os seguintes –
1) Fecho – Se uma expressão booleana envolve certas variáveis que pertencer um conjunto digamos S, então o conjunto S é fechado em relação a um operador binário se para cada par de elementos de S, o operador binário especifica regras para obter um elemento único de S. Em outras palavras, se uma função booleana envolve certas variáveis booleanas , então as variáveis bem como o resultado da expressão booleana deve pertencer a um conjunto comum de elementos. Qualquer expressão booleana sempre seguir fechamento em relação à adição binária (+ operador) e multiplicação binária (. operador).
2) Identidade – Diz-se que um conjunto tem um elemento de identidade para um operador (como *) se existir um elemento, digamos e no conjunto, tal que e pertence ao conjunto e a multiplicação de e com qualquer outro elemento resulta no mesmo elemento, ou seja, se x também pertence a mesmo definido, então x*e = e*x = x. Em um sistema booleano, o elemento de identidade em relação à adição binária é 0, como para qualquer variável booleana, digamos x, x + 0 = 0 + x = x. Da mesma forma, o elemento de identidade em relação à multiplicação binária é 1, como para qualquer variável booleana, digamos x, x.1 = 1.x = x.
3) Comutativo – Qualquer expressão booleana é comutativa em relação à adição binária, bem como à multiplicação binária. Como se existissem duas variáveis booleanas – x e você, então x + y = y + x. Da mesma forma, xy = yx
4) Associativo – Qualquer expressão booleana também é associativa em relação à adição binária, bem como à multiplicação binária. Como se existissem três variáveis booleanas – x, y e z, então x + (y + z) = (x + y) + z. Da mesma forma, x.(yz) = (xy).z.
5) Distributivo – Na álgebra booleana, a adição binária é distributiva sobre a multiplicação binária e a multiplicação binária é distributiva sobre a adição binária. Portanto, se houver três variáveis booleanas – x, y e z, então x.(y + z) = (xy) + (xz). Da mesma forma, x+(yz) = (x+y). (x+z).
6) Inverso – A álgebra booleana não possui inverso aditivo ou multiplicativo, pois não há operações de subtração e divisão na álgebra booleana. Porém, qualquer elemento booleano, digamos x, tem um complemento x' tal que x + x' = 1 e x.x' = 0.
A lei associativa não é um postulado de Huntington, mas é válida para a álgebra booleana. Deve-se notar também que a álgebra booleana possui + operador distributivo sobre. operador. Isso é diferente das leis da álgebra comum. É importante notar também que a álgebra booleana possui complemento, mas não inverso. A álgebra booleana usada na eletrônica digital é uma álgebra booleana de dois valores. É definido sobre um conjunto, digamos B, que possui apenas dois elementos – (0, 1). Todos os postulados mencionados acima são válidos na álgebra booleana de dois valores como segue –
1) Fecho – O resultado de qualquer expressão booleana é 0 ou 1. Portanto, segue a lei de fechamento em relação ao conjunto (0, 1).
2) Identidade – O 0 é o elemento de identidade em relação à adição binária, como para qualquer variável booleana, digamos x, 0 + x = x + 0 = x. Se x = 0, então 0 + 0 = 0 + 0 = 0. Se x for 1, então 0 + 1 = 1 + 0 = 1. O 1 é o elemento de identidade em relação à multiplicação binária como para qualquer variável booleana, digamos x , 1.x = x.1 = x. se x = 0, então 1,0 = 0,1 = 0. se x = 1, então 1,1 = 1,1 = 1.
3) Inverso – O complemento de 0 é 1 e o complemento de 1 é 0. Na adição binária, 0 + 1 = 1 e na multiplicação binária, 0,1 = 0. Para qualquer variável booleana diga x, x + x' = 1 e x.x' = 0.
Princípio da Dualidade –
A dualidade é uma propriedade importante da álgebra booleana. De acordo com esta propriedade, qualquer expressão booleana, dedutível pelos postulados da álgebra booleana (postulados de Huntington junto com a propriedade associativa), permanece a mesma se o operador e os elementos de identidade forem trocados. Portanto, o dual de uma expressão booleana pode ser obtido trocando os operadores AND e OR e substituindo todos os 1 por 0 e 0 por 1.
Teoremas Booleanos –
Qualquer expressão booleana é dedutível pelos seguintes teoremas –
Teorema 1 – Para qualquer variável booleana x, x + x = x e xx = x. Suponha que, se x = 0, então 0 + 0 = 0 e 0,0 = 0. Se x = 1, então 1 + 1 = 1 e 1,1 = 1.
Teorema 2 – Para qualquer variável booleana x, x + 1 = 1 e x,0 = 0. Suponha que, se x = 0, então 0 + 1 = 1 e 0,0 = 0. Se x = 1, então 1 + 1 = 1 e 1,0 = 0.
Teorema 3 (Involução) – Para qualquer variável booleana x, (x')' = x. Suponha que x = 0, então (0′)' = 1′ = 0. Se x = 1, então (1′)' = 0′ = 1.
Teorema 4 (associativo) – Para quaisquer variáveis booleanas x, y e z, x + (y + z) = (x + y) + z e x. (y. z) = (x. y) . z.
Teorema 5 (Teorema de DeMorgan) – Este teorema estabelece a lei da dualidade para a álgebra booleana. Para quaisquer variáveis booleanas x e y, (x + y)' = x' . y' e (xy)' = x' + y'.
Teorema 6 (Absorção) – Para quaisquer variáveis booleanas x e y, x + (x . y) = x e x . (x + y) = x. Isso pode ser provado da seguinte forma –
x + (x. y) = (x. 1) + (x. y)
= x (1 + y)
=x. 1
=x
De forma similar,
x. (x + y) = (x.x) + (x.y)
= x + (x. y)
= (x. 1) + (x. y)
= x (1 + y)
=x. 1
=x
Precedência do operador na álgebra booleana –
A precedência do operador em ordem decrescente na álgebra booleana é a seguinte – 1) Parênteses, 2) NÃO, 3) E e 4) OU. Qualquer expressão booleana é deduzida da esquerda para a direita e a maior precedência é entre parênteses . Depois NOT, AND e por último operador OR.
Função Booleana –
Uma função booleana é uma expressão algébrica booleana que consiste em variáveis booleanas (onde cada variável pode ter um valor 0 ou 1), constantes booleanas (ou seja, 0 e 1) e operadores booleanos (como AND, OR, NOT). Qualquer função booleana representa praticamente algum cálculo em dados binários. Por exemplo, deixe uma função booleana dizer que F seja como –
F = x + yz
Aqui x, y e z são variáveis booleanas (fontes de dados binários como células binárias de um registro) que são relacionadas pelos operadores AND e OR na função acima. Todos os resultados possíveis de uma expressão booleana podem ser representados por uma tabela verdade. A tabela verdade lista todas as combinações possíveis dos valores das variáveis booleanas e comparar com o resultado da expressão booleana. Como para o acima indicado função, o seguinte é a tabela verdade –
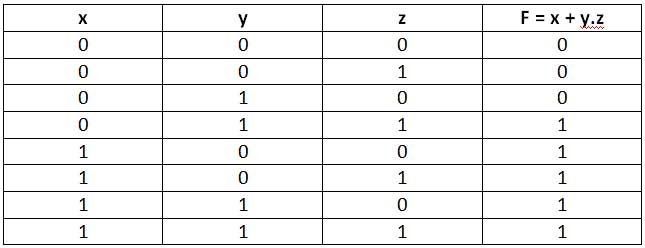
Figura 1: Tabela verdade para uma função booleana
Um circuito digital para a função booleana acima nada mais é do que a interconexão de portas lógicas (AND, OR, NOT) com fontes de dados binárias (representadas por variáveis booleanas na função booleana). A multiplicação binária ou operação de pontos entre duas variáveis é equivalente a conectar duas fontes binárias como entrada da porta AND. A adição binária ou operação de adição entre duas variáveis é equivalente a conectar duas fontes binárias como entrada da porta OR. O complemento equivale a conectar uma fonte binária a uma porta NOT. Portanto, o circuito digital para a função acima será o seguinte –
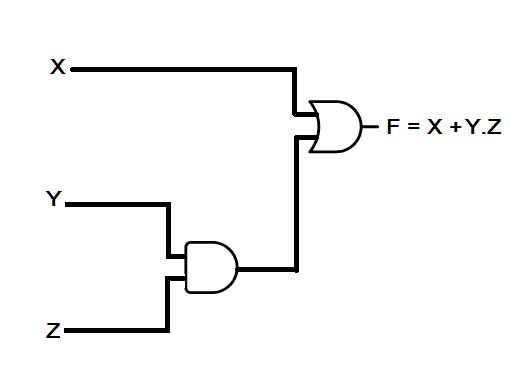
Fig. 2: Imagem mostrando Função Booleana convertida em Circuito Lógico
Complemento de uma função booleana –
O complemento de uma função booleana é obtido trocando todos os 0 por 1 e 1 por 0 e trocando os operadores AND e OR. Em uma função booleana, a substituição de todos os 0 por 1 e de todos os 1 por 0 é feita substituindo as variáveis booleanas por seus complementos. Por exemplo, o complemento da função indicada acima será o seguinte –
Se F = x + yz, então
F' = x' . (y' + z')
Minterm e Maxterm –
Uma variável booleana pode saída em sua forma normal (como x) ou em sua forma complementar (como x') em uma expressão booleana. Se a operação AND for feita entre duas variáveis, digamos x e você, pode haver quatro combinações possíveis – xy, x.y', x'.y e x'.y'. Cada um desses produtos possíveis são chamado Minterm ou produto padrão. Da mesma forma, se a operação OR for feita entre duas variáveis, digamos x e você, então, novamente, existem quatro combinações possíveis – x + y, x + y', x' + y e x' + y'. Cada uma dessas somas possíveis são chamados Maxterm ou somas padrão.
Para duas variáveis, x e y, os seguintes Mintermos e Maxtermos são possíveis –
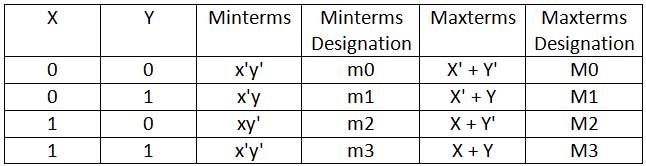
Fig. 3: Tabela listando Mintermos e Maxtermos para duas variáveis booleanas
Da mesma forma, para três variáveis, digamos x, y e z, os seguintes Mintermos e Maxtermos são possíveis –
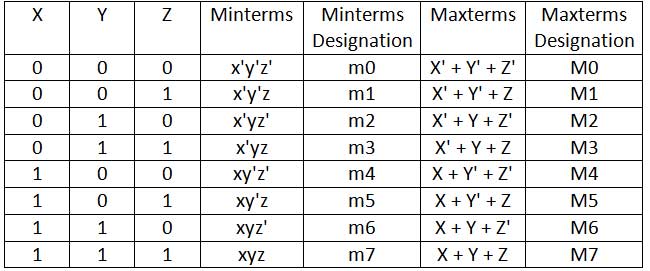
Fig. 4: Tabela listando Mintermos e Maxtermos para três variáveis booleanas
Para n variáveis, podem existir 2^n Mintermos e 2^n Maxtermos. Uma qualquer função booleana pode ser expresso como soma de Mintermos produzindo 1 para a função na tabela verdade ou Produto de Maxtermos produzindo 0 para a função na tabela verdade, desde que a tabela verdade para a função seja conhecida. Por exemplo, existe uma função F, com a seguinte tabela verdade –Da mesma forma, para três variáveis, digamos x, y e z, os seguintes Mintermos e Maxtermos são possíveis –
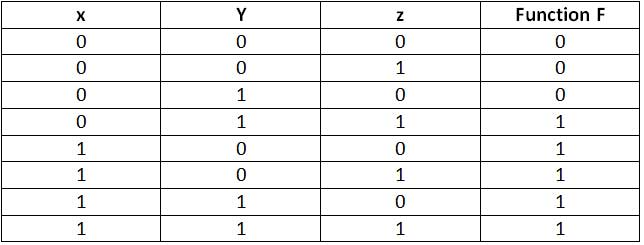
Fig. 5: Tabela verdade para uma função booleana de três variáveis
A partir da tabela verdade acima, a função F pode ser expressa como a soma dos mintermos produzindo 1 para a função na tabela verdade como segue –
F =x'yz + xy'z' + xy'z + xyz' + xyz = m3 + m4 + m5 + m6 + m7A partir da tabela verdade acima, a função F pode ser expressa como a soma dos Mintermos produzindo 1 para a função na tabela verdade como segue –
Da mesma forma, pode ser expresso como produto de Maxtermos produzindo 0 para a função na tabela verdade como segue –
F = (x' + y' + z') . (x' + y' + z) . (x' + y + z') = M0 . M1. M2
Diz-se que uma função expressa como soma de mintermos ou produto de maxtermos está em sua forma canônica. Quanto ao número n de variáveis, pode haver 2^n mintermos e 2^n maxtermos, o número de funções possíveis com n número de variáveis é 2^2n. Portanto, para 2 variáveis booleanas, pode haver 4 mintermos e 4 maxtermos e o número total de funções possíveis com eles é 16. Portanto, pode haver 16 funções binárias (operações binárias) possíveis entre duas variáveis booleanas ou (fontes binárias).
Ao expressar uma função na forma de Mintermos e Maxtermos, ela pode ter implementação de dois níveis em portas lógicas. A implementação em dois níveis é sempre preferida, pois produz ao menos quantidade de atraso através dos portões quando sinal se propaga da entrada para a saída do circuito digital.
No próximo tutorial, conheça todos os possíveis operações lógicas entre duas variáveis booleanas. Existem operações lógicas adicionais além de AND, OR e NOT. Todas as operações lógicas possíveis entre duas fontes binárias podem ser derivadas com o conhecimento de funções booleanas e teoremas.

