O projeto do bloco de pressão foi projetado para absorver as forças causadas pelas mudanças na direção do líquido que flui através dos tubos. Uma mudança no momento cria forças externas nos tubos. Os blocos de pressão são projetados para acomodar essas forças mesmo que não possam ser suportados pelo próprio tubo.
Este artigo discute a literatura sobre design de pilares e um exemplo de design de pilares.
Relatório CRIA 128 Fornece diretrizes abrangentes para o projeto do bloco de pilar.
O método de cálculo está sujeito às seguintes premissas, conforme indicado no Relatório CRIA 128.
- As seções transversais do fluxo são constantes (exceto para cones).
- A perda de viscosidade nos componentes é insignificante, exceto nas válvulas parcialmente fechadas.
- A pressão dinâmica é baixa (as velocidades do fluxo raramente excedem 3 ms-1o que corresponde a uma altura manométrica dinâmica < 0,05 bar).
- A teoria do fluxo unidimensional é válida
- O líquido no tubo é um fluido newtoniano, por exemplo água.
- As forças de impulso de qualquer atrito resultante de uma queda de pressão associada a uma mudança na velocidade do fluxo são consideradas insignificantes para aplicações dentro do escopo deste relatório.
Dois métodos são especificados na diretriz para calcular a força de impulso.


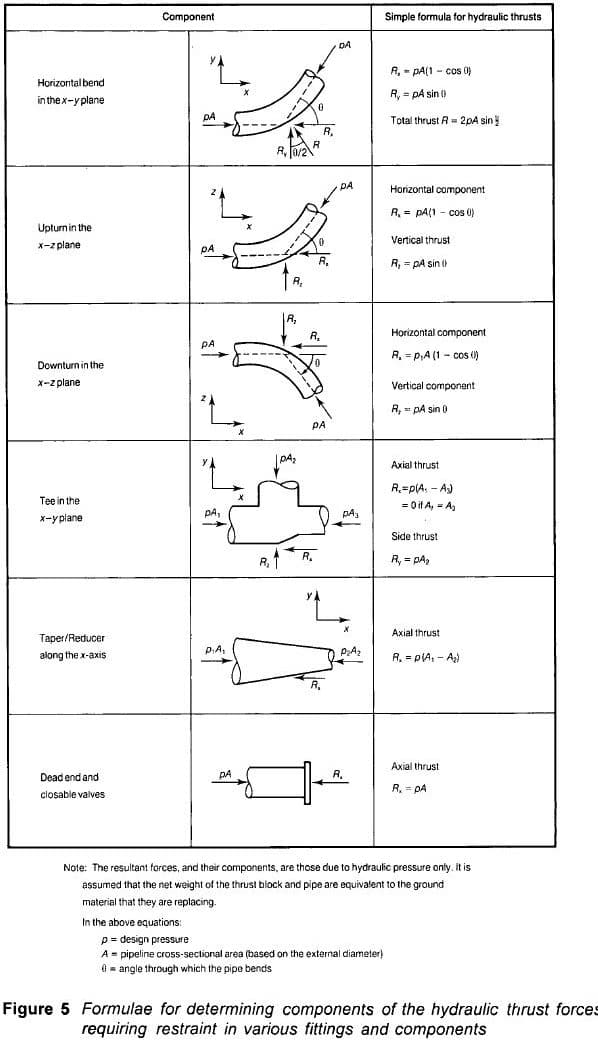
A tabela a seguir e os diagramas associados também podem ser usados para calcular as forças que atuam no bloco de pilar.


Para calcular as forças que atuam no bloco de pressão, você pode usar um dos métodos mencionados acima.
Exemplo de construção de bloco de pressão
A análise e o projeto consideraram as seguintes suposições e dados de projeto.
- Densidade do concreto 24 kN/m3
- Qualidade do concreto classe 25
- Resistência característica mínima do aço 460 N/mm2
- Cobertura para reforço abaixo da borda superior do solo 75mm
- Pressão operacional 6bar (= 600kN/m2)
- Inclinação do tubo 450
- Ângulo de atrito interno 300
- Pressão de suporte permitida 150 kN/m2
- Densidade do solo 18 kN/m3
Nesta seção são realizados o cálculo das cargas no bloco de encosto, o cálculo do peso do bloco de encosto e a verificação da estrutura de suporte e reforço.
CÁLCULO DA RESPOSTA DE UM TUBO DE 1200 MM DE DIÂMETRO
Ângulo do tubo em relação à horizontal = 450
Força horizontal = PA(1-cosθ) = 600 x π x 1,22 (1-cos45)/4 = 200kN
A força horizontal atua na direção do tubo.
Resposta vertical = PA sinθ = 600 x π x 1,22 x (sen45)/4 = 480 kN


Considere a disposição do bloco de impulso conforme mostrado na figura acima. A largura do bloco de pressão é de 2.250 mm e o comprimento é de 2.000 mm.
Peso do concreto = (2,25 x 1,05 x 2 – π x 1,22 x 2 / (2 x 4) ) x 24 = 87 kN
Verifique o armazém
Reação vertical = 480 kN
Como a pressão operacional é levada em consideração no cálculo das forças de impulso, a reação vertical sobrejacente pode ser levada em consideração para controlar o rolamento.
Força vertical SLS = 480 kN
Reação vertical ao solo = 480 + 87 = 567 kN
Área do pilar = 2,25 x 2 = 4,5 m2
Pressão sob a base = 567 / 4,5 = 126 kN/m2
A pressão é inferior à pressão de rolamento permitida (150 kN/m2). Portanto, ok.
Verificando a estabilidade lateral
A mudança no ângulo cria forças verticais e horizontais. As forças horizontais atuam na direção da tubulação. Este cálculo assume que não há forças atuando na tubulação.


Conforme mostrado na figura acima, o tubo é colocado 2 m abaixo da superfície do solo.
Do cálculo acima
Força horizontal no tubo (SLS) = 200 kN
Força de projeto = 1,5 x 200 = 300 kN
Resistência do solo = força devido à diferença de força lateral + resistência da base
Resistência de aterramento = (σP-σA)AF +τbAb
Calcule o coeficiente de pressão de terra ativa = (1-sinθ)/(1+sinθ)
Ka = (1-sen30)/(1+sen30)
Ka = 0,333
Calcule o coeficiente de pressão passiva da terra = (1+sinθ)/(1-sinθ)
Kp = (1+sinθ)/(1-sinθ)
Kp = 1,5
Uma vez que as forças no concreto Bloco e tubo, considere a pressão no meio do tubo.
Pressão ativa = KAγh = 0,333 x 18 x 2 = 12 kN/m2
Pressão passiva = KPγh =3 x 18 x 2 = 108 kN/m2
Superfície lateral = tubo + pilar = 0,6 + 1,05 = 1,65 m
Área lateral = 1,65 x 2 = 3,3 m2
Força de resistência = (108 – 12) x 3,3 = 316,8 kN
Força horizontal aplicada = 300 kN
Portanto, o bloco de pilar é horizontalmente estável. Além disso, a resistência de base não foi considerada neste cálculo. Levar em consideração a resistência da base aumenta ainda mais a resistência.
Além disso, o cálculo acima pode ser verificado da seguinte forma.
Força aplicada SLS = 200 kN
Resistência = 316,8kN
O fator de segurança contra escorregamento = 316,8/200 = 1,58 >1,5
Portanto, ok.