A não linearidade geométrica é um conceito fundamental em engenharia que desempenha um papel crucial na análise e projeto de estruturas. Ao contrário da análise linear, que assume que as estruturas se comportam linearmente sob carga, a não linearidade geométrica é responsável pelas deformações causadas por grandes deslocamentos, rotações e deformações. Neste artigo, exploramos o conceito de não linearidade geométrica, sua importância na engenharia, seu impacto no comportamento estrutural e suas diversas aplicações.
Na análise técnica, muitas vezes assume-se que as estruturas reagem linearmente às forças externas. Contudo, em cenários reais, esta suposição pode não ser verdadeira quando se trata de grandes deformações ou sistemas altamente flexíveis. A não linearidade geométrica leva em consideração as mudanças na geometria que ocorrem como resultado dessas deformações, permitindo uma representação mais precisa da resposta estrutural.
Compreendendo a não linearidade geométrica
A não linearidade geométrica refere-se ao desvio da linearidade na geometria de uma estrutura quando ela é submetida a cargas ou deslocamentos significativos. Este desvio é causado pelas grandes rotações, deslocamentos e deformações a que a estrutura está sujeita. É importante considerar a não linearidade geométrica quando os deslocamentos e rotações se tornam comparáveis ao tamanho da estrutura ou quando as cargas aplicadas provocam deformações significativas.
Importância da não linearidade geométrica na engenharia estrutural
A não linearidade geométrica é de extrema importância na engenharia por vários motivos.
Primeiro, os engenheiros podem prever com precisão o comportamento das estruturas sob grandes deformações. A análise linear não captura efeitos não lineares que podem levar a falhas inesperadas ou catastróficas. Ao levar em conta as não linearidades geométricas, os engenheiros podem avaliar de forma mais confiável a estabilidade, a resistência e o desempenho geral das estruturas.
Em segundo lugar, a não linearidade geométrica desempenha um papel crucial no processo de otimização do projeto. Negligenciar a não linearidade geométrica pode resultar em projetos excessivamente conservadores ou estruturas propensas a erros. Ao levar em conta a não linearidade geométrica, os engenheiros podem otimizar o projeto, reduzir o consumo de material e melhorar a eficiência geral da estrutura.
Efeitos da não linearidade geométrica
A não linearidade geométrica leva a diversos efeitos que influenciam significativamente o comportamento das estruturas. Esses efeitos incluem:
1. Grandes deformações e rotações:
Com a não linearidade geométrica, as estruturas podem sofrer deformações e rotações significativas. Isto pode levar a mudanças na rigidez, alterações na distribuição de tensões e instabilidade potencial.
2. Redistribuição de carga:
A não linearidade geométrica pode levar à redistribuição de carga dentro de uma estrutura. Quando ocorrem deformações, as forças e momentos são redistribuídos, o que afeta a estrutura geral. Resposta estrutural. Além disso, a capacidade de suporte insuficiente do elemento estrutural pode levar a falhas estruturais devido ao aumento das forças.
3. Comportamento de flambagem e pós-flambagem:
A não linearidade geométrica desempenha um papel significativo no comportamento de flambagem e pós-flambagem das estruturas. Quando as deformações de uma estrutura tornam-se grandes, a suposição de pequenos deslocamentos e deformações inerentes à análise linear não é mais válida. A não linearidade geométrica é responsável pelas mudanças na geometria que ocorrem quando uma estrutura se deforma, resultando em comportamento não linear.
Flambagem é a falha repentina ou colapso de uma estrutura devido ao equilíbrio instável. A não linearidade geométrica afeta o comportamento de flambagem, introduzindo deformações adicionais e mudanças de forma quando a estrutura atinge cargas críticas. Numa análise linear, a carga de flambagem é determinada unicamente pelas propriedades do material e da rigidez da estrutura. Contudo, na presença de não linearidade geométrica, a carga crítica também depende da forma inicial e das condições de contorno.
O comportamento pós-encurvadura descreve a reação de uma estrutura após a encurvadura. A não-linearidade geométrica afeta o comportamento pós-encurvadura, introduzindo grandes deformações e alterações na rigidez. Após a flambagem, a estrutura passa por uma série de configurações de equilíbrio à medida que se adapta às novas condições de carregamento. O comportamento pós-encurvadura pode ter formas complexas, deformações locais e interações entre diferentes tipos de deformação.

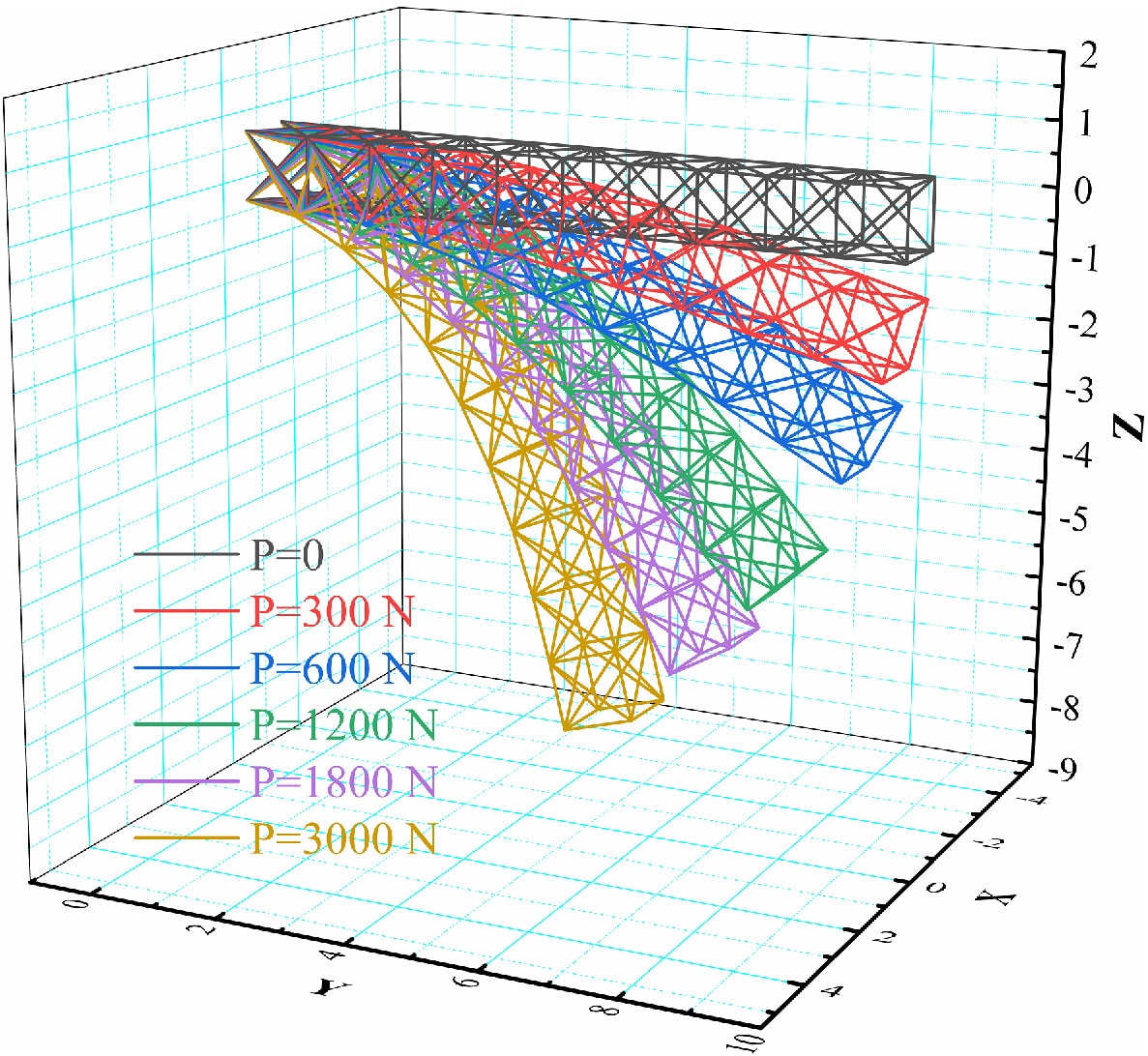
Modelagem matemática da não linearidade geométrica
Modelos matemáticos são utilizados para analisar e prever o comportamento de estruturas sob não linearidade geométrica. Estes modelos levam em consideração as relações não lineares entre deslocamentos, rotações e cargas aplicadas. A análise de elementos finitos (FEA) é uma técnica amplamente utilizada para modelar não linearidade geométrica. FEA discretiza a estrutura em pequenos elementos, permitindo uma representação precisa da geometria complexa e do comportamento não linear.
Vários modelos constitutivos são usados para descrever a resposta do material em caso de não linearidade geométrica. Esses modelos levam em consideração fatores como endurecimento, grandes deformações e relações tensão-deformação. As equações de equilíbrio não linear são resolvidas iterativamente para encontrar os deslocamentos, rotações e forças internas que satisfazem as condições de equilíbrio.
Técnicas de análise para problemas geometricamente não lineares
A análise de problemas geométricos não lineares requer técnicas especializadas que vão além da análise linear tradicional. Algumas técnicas comumente usadas são:
1. Métodos incrementais-iterativos:
Esses métodos dividem a análise em pequenos incrementos e resolvem iterativamente as equações de equilíbrio em cada incremento. A abordagem incremental garante que os efeitos não lineares sejam capturados com precisão.
2. Controle de carga ou caminho:
Na análise geométrica não linear, o carregamento pode ser controlado por forças aplicadas ou deslocamentos prescritos. Isto permite examinar diferentes cenários de carregamento e avaliar a resposta da estrutura sob diferentes condições.
3. Análise de flambagem não linear:
A não linearidade geométrica influencia significativamente o comportamento de flambagem das estruturas. A análise de flambagem não linear identifica cargas críticas e modos de falha correspondentes, fornecendo assim informações sobre a estabilidade estrutural.
4. Análise Dinâmica:
A não linearidade geométrica pode ter efeitos significativos no comportamento dinâmico das estruturas. Técnicas de análise dinâmica, como análise modal ou análise de histórico de tempo, levam em consideração os efeitos do comportamento não linear nas frequências naturais, formas modais e respostas dinâmicas.
Em resumo, a não linearidade geométrica é um aspecto crucial da análise de engenharia que leva em conta as deformações e rotações que ocorrem em estruturas sob cargas significativas. É importante compreender e levar em conta a não linearidade geométrica para garantir previsões precisas do comportamento estrutural e otimizar projetos.
Aplicações de não linearidade geométrica
A não linearidade geométrica tem aplicações em diversas áreas da engenharia. Algumas aplicações notáveis são:
1. Planejamento estrutural:
A não linearidade geométrica é de extrema importância na engenharia civil. Desempenha um papel importante na análise e projeto de estruturas como pontes, edifícios e componentes aeroespaciais. A contabilização da não linearidade geométrica ajuda a garantir a segurança estrutural, a estabilidade e o desempenho sob condições de carregamento realistas.
2. Engenharia mecânica:
Na engenharia mecânica, a não linearidade geométrica é crucial para a análise de mecanismos, componentes mecânicos e sistemas mecânicos. Ajuda a compreender o comportamento de corpos flexíveis, conexões e ligações, levando a um melhor desempenho e confiabilidade.
3. Modelagem de materiais:
A não linearidade geométrica está intimamente relacionada ao comportamento e à deformação do material. É usado na modelagem de materiais para representar com precisão fenômenos não lineares como plasticidade, viscoelasticidade e hiperelasticidade. Modelos de materiais com não linearidade geométrica permitem simulações e previsões mais realistas.
4. Dinâmica de Fluidos Computacional (CFD):
As simulações de CFD muitas vezes precisam considerar os efeitos da não linearidade geométrica, particularmente em problemas de interação fluido-estrutura. A não linearidade geométrica influencia o comportamento de estruturas flexíveis no fluxo de fluidos e fornece insights sobre a dinâmica e estabilidade de sistemas como plataformas offshore, turbinas eólicas e asas de aeronaves.
5. Biomecânica:
A não linearidade geométrica desempenha um papel significativo na análise de estruturas biológicas, como ossos, tecidos moles e órgãos. Ajuda a compreender a deformação e a resposta destas estruturas sob diferentes condições de carga e apoia a investigação médica, o desenho de próteses e as simulações cirúrgicas.
Perguntas frequentes
Qual é a diferença entre análise linear e geométrica não linear?
A análise linear assume que as estruturas se comportam linearmente sob carga, desprezando os efeitos de grandes deformações e rotações. A análise geométrica não linear considera as relações não lineares entre deslocamentos, rotações e cargas aplicadas, permitindo uma representação mais precisa do comportamento estrutural.
Que influência a não linearidade geométrica tem na estabilidade estrutural?
A não linearidade geométrica pode afetar a estabilidade estrutural, causando flambagem, alterando formas modais e redistribuindo forças e momentos dentro da estrutura. Negligenciar a não linearidade geométrica pode levar à subestimação de cargas críticas e possíveis falhas estruturais.
A não linearidade geométrica pode ser ignorada na análise de engenharia?
Em muitos cenários de engenharia que envolvem grandes deformações, rotações ou estruturas flexíveis, a não linearidade geométrica não pode ser ignorada. Negligenciar a não linearidade geométrica pode levar a previsões imprecisas, comprometimento da segurança e projetos ineficientes.
Existem ferramentas de software para lidar com problemas geometricamente não lineares?
Sim, existem diversas ferramentas de software que podem resolver problemas geometricamente não lineares. Essas ferramentas utilizam métodos numéricos avançados e fornecem recursos para modelagem, simulação e análise de estruturas sob não linearidade geométrica. Exemplos incluem Abaqus, ANSYS e LS-DYNA.
Quais são alguns exemplos da vida real em que a não linearidade geométrica desempenha um papel significativo?
Exemplos do mundo real onde a não linearidade geométrica desempenha um papel incluem a análise de edifícios altos expostos ao vento e sísmico cargas, a construção de pontes e arcos curvos, a simulação de robôs manipuladores flexíveis e o estudo da mecânica das válvulas cardíacas em engenharia biomédica.

