Para entender melhor a funcionalidade e o desempenho de um filtro, existem funções matemáticas que representam teoricamente um filtro, como função de transferência, fator de qualidade e frequência de corte. A compreensão desses termos facilitará a compreensão de uma propriedade de filtro.
Terminologias (definições)
Função de transferência: As entradas e saídas de um circuito de amplificador operacional podem ser tensões, correntes ou uma combinação das duas. Quando você usa números complexos para as grandezas de entrada e saída, a relação entre saída e entrada torna-se uma função da frequência. O nome da razão é função de transferência.
Transformada de Laplace: A transformada de Laplace é usada para resolver equações diferenciais, a transformada de Laplace converte a equação diferencial em um problema algébrico que é relativamente fácil de resolver.
Sistema variante de tempo: o atraso ou avanço de tempo no sinal de entrada altera não apenas a saída, mas também os outros parâmetros.
Função de transferência
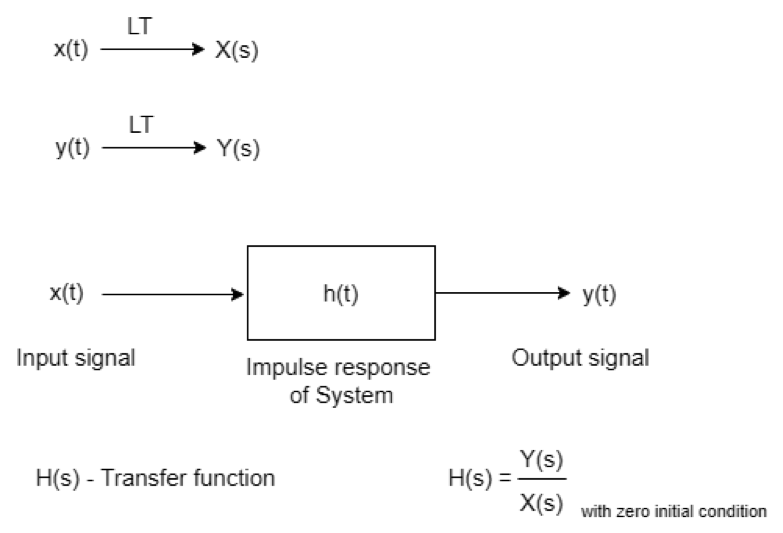
A função de transferência é a razão entre a transformada de Laplace da saída e a transformada de Laplace da entrada quando todas as condições iniciais são consideradas zero. A função de transferência não pode ser definida se a condição inicial não for considerada zero.
Condições iniciais zero significam que o sistema deve ser linear, já que sistemas lineares variantes no tempo são usados na prática.
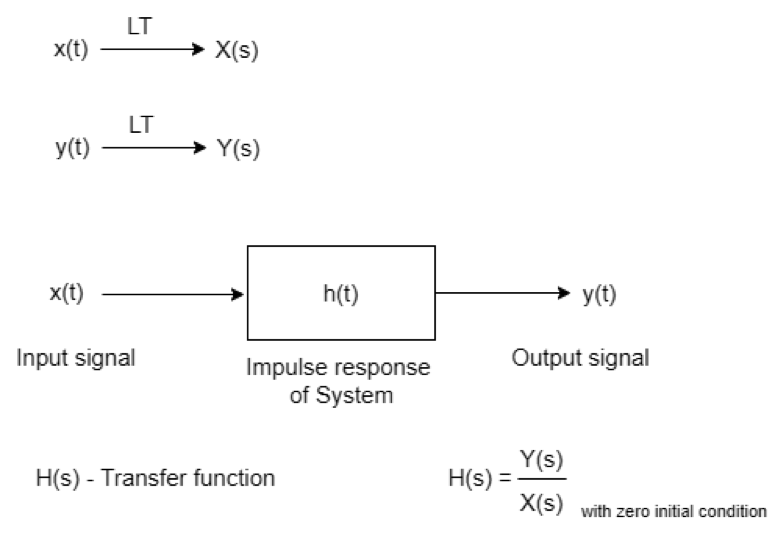
Figura 1 Diagrama de blocos da função de transferência.
Devido à impedância de um indutor ou capacitor, os filtros têm uma resposta dependente da frequência que muda com a frequência.
Como os sinais variantes no tempo são usados na prática, e esses sinais passam por um circuito (filtração, amplificação, atenuação), existe a possibilidade de que esses sinais sejam afetados pelos componentes (indutor, capacitor e resistores) usados no o circuito. E filtros são usados para atenuar alguma parte da frequência do sinal.
Como sabemos, w as impedâncias de um capacitor e de uma indução, respectivamente, são
Zc = 1/sC
Zeu = sL
Plano S s = ó +jù
O plano S é um plano complexo (que possui componentes reais e imaginários) em matemática no qual a transformada de Laplace pode ser plotada.
Onde ó frequência neper, nepers por segundo (NP/s)
ù frequência angular (rad/s)
A função de transferência do filtro pode ser desenvolvida usando técnicas padrão de análise de circuitos. Essas técnicas são as leis de tensão e corrente de Kirchoff, a lei de Ohm e a superposição. Como sabemos que as impedâncias são complexas, então a função de transferência será
H(s) = euéeu + umm-1ém-1 +…+ uma1s + uma0 bnén +bn-1én-1 +…+b1s + b0
Onde m é o grau do numerador, n é o grau do denominador e H(s) é a função racional de s.
O grau do denominador é chamado de ordem do filtro. Ao resolver a equação acima, você obterá raízes que determinam os zeros (numerador) e os pólos (denominador) do circuito do filtro. Cada pólo fornece uma resposta de -6 dB/oitava ou -20 dB/década e cada zero fornece uma resposta de +6dB/oitava ou +20 dB/década. As raízes calculadas da função de transferência podem ser reais ou complexas. Se forem complexas, então as raízes são traçadas no plano s (o plano complexo) onde o eixo horizontal é real (ó,) e o eixo vertical é o eixo imaginário (ù). A distribuição das raízes no plano s ou plano complexo nos diz muitas coisas sobre o circuito do filtro. Para haver estabilidade no sistema, todos os pólos devem estar no lado esquerdo do plano complexo. Zero na origem significa que há zero no numerador, o que significa que o filtro não terá resposta em CC.
Vamos considerar o circuito RLC e escrever uma função de transferência para isso.

A tensão no resistor é
H(s) = VoVin = RCsLCs2 + RCs +1)
Se R = 10, L =10mH, C=10uF então substituindo os valores dos componentes.
H(s) = 103 x(s2 + 103s + 107)

Após a fatoração,
H(s) = 103 x (s(s-(-0,5+j3,122)x103) x (s-(-0,5-j3,122)x103))
AA equação acima fornece um zero na outra origem e pólo em:
S = (-0,5±j3,122)x 103
O plano acima mostra esses pontos.
Em aplicações reais, na maioria dos casos, estamos mais interessados no desempenho do circuito de hardware. Mas também devemos olhar para o plano s do filtro, Neper e frequências imaginárias.
Frequência de corte (F0) e fator de qualidade (Q)
Trabalhar com um plano S não é tão conveniente, então surge a pergunta por quê? A resposta é: é necessário conhecer a função de transferência para entender o fator de qualidade e a frequência de corte.
Frequência de corte (F0)
A frequência de corte é a frequência a partir de onde o filtro começa a filtrar o sinal, então a frequência de corte em um filtro passa-baixa é a frequência a partir de onde o filtro começa a remover as altas frequências, a frequência de corte na verdade é o ponto onde o nível de saída é 3 dB inferior ao nível de entrada, portanto não é exatamente o ponto onde o filtro começa a funcionar.

A frequência de corte é um limite na resposta de frequência de um sistema; a energia que flui através do sistema começa a ser reduzida, atenuada ou refletida em vez de passar. Normalmente, em sistemas eletrônicos, como filtros e canais de comunicação, a frequência de corte se aplica a uma borda nas características passa-baixo, passa-alto, passa-banda ou parada de banda de uma frequência que caracteriza um limite entre a banda passante e a banda final. Às vezes é levado ao ponto na resposta do filtro, onde a banda de transição e a banda passante se encontram.
A frequência de corte é definida, em geral, como a frequência na qual a resposta do filtro está 3dB abaixo da banda passante. A frequência na qual a relação (saída/entrada) tem uma magnitude de 0,707. Se você converter essa magnitude para decibéis, obterá -3dB, o que significa um ponto negativo de 3dB.
dB = 20 log (0,707)
A quantidade de atenuação do filtro começa a aumentar rapidamente neste ponto, conforme mostrado na figura abaixo.

Fator de qualidade (Q)
O fator de qualidade é a medida do pico do filtro. Q é realmente válido apenas para o filtro de segunda ordem e não é válido para sistemas de primeira ou terceira ordem. O fator de qualidade é definido como a queda de potencial no indutor ou capacitor até a queda de potencial no resistor.
Q = (Queda de tensão em “L”)/ (queda de tensão em “R”)
Ou
Q = (queda de tensão em “C”) / (queda de tensão em “R”)
Cálculo do fator de qualidade para indutor:
Q = (eu Xeu ) / (eu R)
Q = Xeu / R = wL / R
Q = 2pfL/R
f é a frequência de ressonância, f = 1/2p sqrt (LC)
Q = (1/R) quadrado(L/C)
Da mesma forma, o fator de qualidade de um capacitor também é calculado, que também é,
Q = (1/R) quadrado(L/C)
Para um circuito RC, LR ou RLC, a função de transferência será a mesma da equação acima.
O fator de qualidade é o quão subamortecido é um ressonador, o que significa a rapidez com que uma oscilação desaparece.
Q é o fator de qualidade, e a função de transformação do fator de qualidade é expressa como
α = 1/Q
Se Q > 0,707, haverá pico na resposta do filtro.
Se Q <0,707, role em f0 será maior.