
Atualmente, as fórmulas de cálculo da força de flexão amplamente utilizadas foram adotadas de fontes estrangeiras sem qualquer informação sobre sua origem ou escopo de aplicação.
Este artigo apresenta uma análise sistemática do processo de derivação da fórmula de cálculo da força de flexão, bem como dos parâmetros requeridos.
Além disso, é introduzida uma nova abordagem para calcular a força de flexão para ampliar o seu âmbito de aplicação.
Calculadora de força de flexão em forma de V e U
Fórmula de força de flexão de chapa metálica
Nos últimos anos, a máquina dobradeira ganhou ampla utilização em vários setores e expandiu suas capacidades de processamento.
Apesar de sua popularidade, tem havido uma falta de discussão sistemática sobre o cálculo da força de flexão.
Atualmente, existem aproximadamente dois tipos de fórmulas de cálculo de força de flexão recomendadas pelos manuais de produtos de diferentes fabricantes de dobradeiras.
Na fórmula:
- P- força de flexão, kN;
- S- espessura da chapa, mm;
- eu –comprimento de dobra da folha, m;
- V- largura da abertura inferior da matriz, mm;
- σb– resistência à tração do material, MPa.
A fórmula recomendada para cálculo da força de flexão pelo fabricante é baseada em uma fórmula mencionada anteriormente.
Ambas as fórmulas foram retiradas de vários folhetos de produtos, no entanto, não há provas de sua precisão.
Calculadora relacionada: Calculadora de tonelagem do freio de imprensa
O processo de obtenção da fórmula de cálculo da força de flexão, bem como seu escopo aplicável.
A Figura 1 é uma representação esquemática do processo de dobramento de uma chapa.
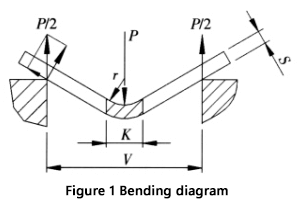
- P: Força de flexão
- S: Espessura da folha
- V: Largura da abertura inferior da matriz
- r: Raio interno durante o processo de dobra
- K: Largura da projeção horizontal da zona de deformação durante a flexão.
O cálculo da força de flexão e seus parâmetros são explicados a seguir:
A largura recomendada da abertura inferior da matriz (V) para flexão livre é de 8 a 10 vezes a espessura da chapa (S), com uma relação largura/espessura de V/S = 9.
Os fabricantes de prensas dobradeiras fornecem os valores da largura da matriz (V) e do raio interno (r) da peça dobrada em sua tabela de parâmetros de força de flexão. A relação raio-largura é geralmente r = (0,16 a 0,17) V e, neste caso, o valor de 0,16 é usado.
Durante o processo de flexão, o material na zona de deformação sofre uma deformação plástica significativa, fazendo com que ele se dobre em torno da linha central.
Em alguns casos, podem aparecer pequenas fissuras na superfície externa da área curva.
A tensão na zona de deformação, exceto próximo à camada central, está próxima da resistência à tração do material, com a parte superior da camada neutra sendo comprimida e a parte inferior sob tensão.
A Figura 2 ilustra a seção transversal e o diagrama de tensões correspondente na zona de deformação.
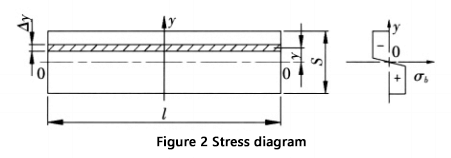
- Espessura da folha S
- l- comprimento de dobra da folha
O momento fletor na seção da zona de deformação é:
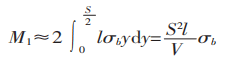
O momento fletor produzido pela força fletora na zona de deformação é mostrado na Figura 1.
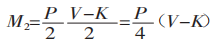
De1 =M2Nós temos:

Ao dobrar uma chapa com um molde universal em uma dobradeira, conforme mostrado na Figura 3, a maioria das chapas é dobrada em 90°. Neste caso, K é:
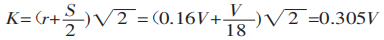
Substituindo K na equação (1), obtemos:
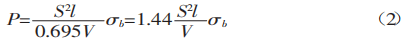
A resistência à tração dos materiais comuns, σb, é 450 N/mm². Este valor pode ser usado na fórmula (2) para calcular o resultado.
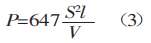
A fórmula de cálculo da força de flexão aqui obtida está de acordo com as informações fornecidas em folhetos estrangeiros.
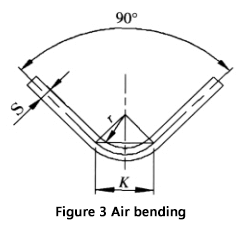
As variáveis na fórmula são:
- S: Espessura da folha
- r: Raio interno quando a folha é dobrada
- K: Largura da projeção horizontal da zona de deformação por flexão.
Como pode ser visto no processo de derivação, ao usar as fórmulas (2) ou (3) para calcular a força de flexão, é importante garantir que duas condições adicionais sejam atendidas: a relação entre largura e espessura (V/S) deve ser igual a 9, e a relação entre o raio e a largura deve ser igual a 0,16.
Se estas condições não forem satisfeitas, poderão ocorrer erros significativos.
Novos métodos e etapas para calcular forças de flexão
O cálculo da força de flexão pode ser complicado quando não é possível atender aos dois requisitos adicionais (relação largura/espessura V/S = 9 e relação raio/largura = 0,16) devido a limitações de projeto ou processo.
Nessas situações, é aconselhável seguir estes passos:
- Calcule a relação largura-espessura e a relação raio-largura com base na espessura da placa (S), raio de curvatura (r) e abertura inferior da matriz (V).
- Determine a largura de projeção da zona de deformação considerando a deformação da chapa.
- Use a fórmula (1) para calcular a força de flexão, levando em consideração quaisquer diferenças no raio de curvatura e na zona de deformação correspondente.
Essas etapas fornecerão um resultado mais preciso e confiável em comparação com o uso da fórmula comumente usada. Um exemplo para ilustrar esse processo é mostrado na Figura 4.
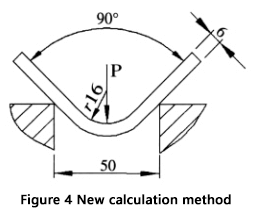
Dado: Espessura da chapa (S) = 6mm, Comprimento da chapa (l) = 4m, Raio de curvatura (r) = 16mm, Largura inferior da abertura da matriz (V) = 50mm e Resistência à tração do material (σb) = 450N/mm².
Pergunta: Como podemos calcular a força de flexão necessária para flexão a ar?
Aqui estão as etapas:
Primeiro, calcule a proporção entre largura e espessura e a proporção entre raio e largura:
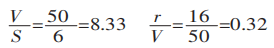
Em seguida, calcule a largura projetada da área de deformação:
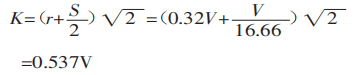
Finalmente, use a fórmula (1) para calcular a força de flexão:
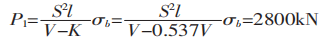
Se a fórmula normalmente recomendada for usada para calcular a força de flexão:
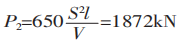
Pode-se inferir de P1/P2 = 1,5 que a diferença entre P1 e P2 é de 1,5 vezes.
A razão para esta discrepância é porque neste exemplo o raio de curvatura é relativamente grande, o que resulta num aumento da área deformada e, portanto, requer uma maior força de flexão.
A relação entre raio e largura neste exemplo é 0,32, o que supera os critérios mencionados anteriormente.
Usar a fórmula padrão para calcular a força de flexão não é adequado para este cenário. As vantagens da utilização do novo método de cálculo podem ser observadas neste exemplo.
Além disso, existe uma calculadora online disponível para calcular a força de flexão usando o novo método.
Tabela de resistência à tração
| Material | Resistência à tracção | ||
|---|---|---|---|
| americano | europeu | China | N/mm² |
| 6061 Alumínio | Alu50 | LD30 | 290 |
| 5052 Alumínio | Alu35 | LF2 | 303 |
| 1010 aço macio | DC01 | 10/10F | 366 |
| A 536 -80 G 60-40-18 | GGG-40 | QT400-18 | 400 |
| A 351 G CF 8 | GX 6CrNi 18 9 | Q235 | 450 |
| Um 572 G50 | S 355MC | Q345 | 550 |
| 304 Inox | Inox V2A | 0Cr18Ni9 | 586 |
| 316 Inox | Inox V4A | 0Cr17Ni12Mo2 | 600 |
| 4140 Baixa liga | 42CrMo4 | 42CrMo | 1000 |
Fórmulas de cálculo de força de flexão para cunhagem
As fórmulas para calcular os parâmetros de cunhagem são diferentes das fórmulas de flexão a ar.
1. Largura da matriz em V:
V = espessura da chapa metálica × 5
2. O raio interno é determinado pela ponta do punção, que deve ser escolhida de acordo com a seguinte fórmula:
Raio = espessura da chapa metálica × 0,43.
3. Força necessária para cunhar:
F(kn/m) = Espessura2×1,65×Resistência à tração (N/mm2)×4,5/Largura Vee da matriz
4. A fórmula de cálculo da aresta interna mínima permanece a mesma:
Borda interna mínima = Die vee × 0,67
Fórmulas de cálculo de força de flexão para dobra Z
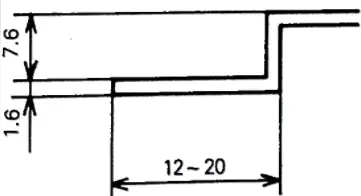
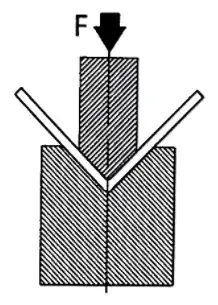
Algumas ferramentas precisam de uma força específica para ceder a chapa metálica e gerenciar o retorno elástico para obter o perfil necessário.
Como exemplo consideraremos ferramentas joggle, que fazem duas dobras ao mesmo tempo com uma curta distância entre a dobra e a contracurvatura.
Como essas ferramentas fazem duas dobras ao mesmo tempo, o retorno elástico deve ser completamente cancelado por cunhagem.
A equação para calcular a força necessária é:
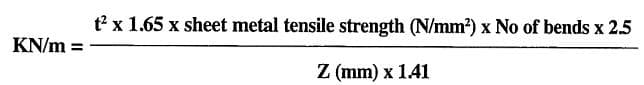
- KN/m = força necessária por metro
- Z = oscilação em mm
- Número de curvas = para um Z, assuma 2
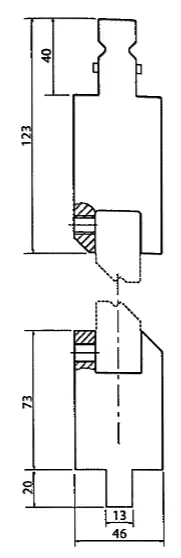
As ferramentas Joggle geralmente consistem em um suporte de inserção no qual as ferramentas Joggle escolhidas de acordo com o joggle e o ângulo necessário são fixadas com parafusos sem cabeça.
É importante consultar o fabricante antes de comprar, pois estes sistemas só podem dobrar chapas finas, no máximo 2mm, mas a espessura máxima dependerá do tipo de pastilha e pode ser inferior a 2mm.
Conclusão
As fórmulas e etapas fornecidas para calcular a força de flexão são adequadas não apenas para flexão angular de uma chapa, mas também para flexão em forma de arco (que tecnicamente deve ser chamada de flexão angular com grande raio de curvatura).
É crucial ter em mente que formar um formato de arco requer um design de molde exclusivo.
Ao projetar a área de deformação, o cálculo deve ser baseado nos parâmetros de processo estabelecidos durante o processo, os quais não podem ser determinados através de uma única fórmula.
Em uma fábrica específica de torres de ferro, dobramos com sucesso um cilindro com espessura de parede de 12 mm, diâmetro de 800 mm e comprimento de 16 m usando uma prensa dobradeira de 28.000 kN e um molde circular.
O método descrito neste artigo foi utilizado para determinar a força de flexão e produziu resultados satisfatórios ao projetar um molde para formato de arco.
Leitura adicional:
- Gráfico de força de flexão aérea: os dados mais confiáveis de Amada

























































