O exemplo de projeto de viga de aço trabalhado explica a construção de uma viga simplesmente apoiada com uma carga uniformemente distribuída. A viga é considerada simplesmente apoiada e os dados de projeto para cálculo do momento fletor e das forças cortantes são fornecidos a seguir.
Além disso, as propriedades da seção transversal a serem consideradas são especificadas nas etapas individuais do teste.
Aspectos teóricos e procedimentos de design de código são discutidos no artigo Design Vigas de aço em conformidade com BS 5950.
Dados de design
- Carga UDL 20 kN/m
- Extensão do feixe 6m
- A viga é simplesmente apoiada
- Resistência de projeto do aço, Py = 275 N/mm2
Momento fletor máximo
= wl2/8 = 20 x 62 / 8 = 90 kN·m
Força de cisalhamento máxima
= wl/2 = 20 x 6/2 = 60 kN
Considere transportador universal 500x200x89,7 kg/m (Pj = 275 N/mm2 )
Dados da seção
- T = 500mm
- T = 16mm
- t = 10mm
- B = 200mm
- b = 100 mm
- R1 = 20 mm
- d = 500 – 16 x 2 – 2 x 20 = 428 mm
- SX = 2175 × 103 milímetros3
- ZX = 1914 × 103 milímetros3
- Rj = 43,3 mm
Vamos começar a calcular o projeto da viga de aço. Como parte deste cálculo do projeto da viga de aço, são realizados os seguintes testes.
- Classificação da seção
- Projeto de cisalhamento
- Construção para flexão
- Verifique se há flambagem por torção
- Controle de deflexão
- Teste de rolamento de ponte
- Prova de flambagem da web
Classificação da seção
O primeiro passo no projeto de uma viga de aço é classificar a seção transversal para determinar se ela é plástica, semiplástica, compacta ou esbelta.
T = 16 mm, Pj = 275 N/mm2
ε = (275/Pj)0,5 = 1
Verifique o flange
b/T = 100/16 = 6,25 < 9ε = 9 – Flange é de plástico
Verifique a web
d/t = 428/10 = 42,8 < 80ε = 80 – A rede é feita de plástico
Além disso, d/t < 70ε = 70 - portanto, nenhuma verificação de flambagem por cisalhamento é necessária
Portanto, A seção é de plástico
Projeto para forças de cisalhamento
Força de cisalhamento de projeto, Fcontra = 60kN
Pcontra = 0,6pj Acontra = 0,6pj tD = 0,6 x 275 x 10 x 500 x 10-3 = 825kN
Fcontra
contra A capacidade de cisalhamento está OK
Dependendo da força de cisalhamento, a construção da viga de aço decide se a seção transversal será exposta a uma força de cisalhamento baixa ou alta.
Construção flexível
Verifique se a seção está sujeita a cisalhamento baixo ou alto
60% x pcontra = 0,6 x 825 = 495kN
Fcontra <0,6Pcontra Seção de baixo cisalhamento
MC deve ser inferior a 1,2PjZX ou Pj SX de acordo com a Seção 4.2.5.1 e Seção 4.2.5.2
MC ≤1,2PjZX = 1,2x275x1914x103 x 10-6 = 613,62 kN·m
MC =Pj SX = 275 x 2175 x 103 x 10-6 = 598,125 kN·m
Portanto,
MC = 598,125 kNm > 90 kNm
Dobrando bem
Detectar flambagem por flexão e torção
MX < Mb /MLT
Nenhuma restrição intermediária foi considerada neste exemplo
MLT = 0,925, Tabela 18, BS 5950
Mb =Pb SX Seção 4.3.6.4
Existem dois métodos para verificar a encurvadura por torção lateral, conforme descrito no artigo Construção de vigas de aço de acordo com BS 5950. Estes são o método estrito e o método simplificado.
Neste exemplo de projeto de viga de aço, discutimos ambos os métodos para explicar melhor os procedimentos que precisam ser seguidos em ambos os métodos.
Mais e além A principal diferença entre esses dois métodos é a avaliação da resistência à flexão.
Método rigoroso
Mb =Pb SX
Pb depende de λLT e Pj
λLT =uvλ√(βeu)
λ = euE /Rj
ME – retirado da Tabela 13 de acordo com a Seção 4.3.5.1 e levando em consideração LLT = L – vão
ME = 1,0LLT = 1 x 6 = 6 metros
λ = euE /Rj = 6.000/43,3 = 138,568
A seção 4.3.6.8 aplica-se aos perfis laminados I e H
x = D / T usado com u = 0,9
x = D / T = 500/10 = 50
βeu pode ser encontrado na seção 4.3.6.9
βeu = 1 para perfis plásticos de classe 1 ou perfis compactos de classe 2
v – fator de esbeltez, que é determinado na Tabela 19 com base em λ / x e η
λ/x = 138,568/50 = 2,771
η = 0,5 para flanges isósceles
v = 0,919 da Tabela 19
λLT =uvλ√(βeu) = 0,9 x 0,919 x 138,568 x √(1) = 114,6
λELA pode ser encontrado na Tabela 16 (ver tabela abaixo)
Se λELA ≥λLT ; Pb =Pj ou então Pb podem ser encontrados na Tabela 16 para perfis laminados.
Se λELA ≥λLT Não é necessário levar em conta a encurvadura por torção; caso contrário, deve ser feita uma verificação da encurvadura por torção.
Pj = 275 N/mm2 ; λELA = 37,3
λELA <λLT Portanto, verifique se há flambagem por torção
Da Tabela 16 para λLT = 114,6; Pb = 102 N/mm2
Mb =Pb SX = 102 x 2175 x 103 x 10-6 = 221,85 kN·m
Mb /MLT = 221,85 / 0,925 = 239,838 kNm
Portanto, MX = 90kNm
seção é suficiente.
Método simplificado
Nota: Não é necessário utilizar ambos os métodos ao dimensionar uma viga. Basta seguir o método simplificado ou rigoroso.
Mb =Pb SX : Parágrafo 4.3.7
Com este método a determinação do Pb é diferente do método anterior. Este método fornece respostas conservadoras. Pb pode ser encontrado na Tabela 20 da BS 5950 com base em √(βeu) (EUE /Rj ) e D/T
βeu = 1; cálculo anterior
ME /Rj = 138,568; cálculo anterior
√(βeu) (EUE /Rj ) = 10,5 x 135,568 = 138,568
D/T = 500/16 = 31,25
Pb = 116,646 N/mm2 Da tabela 20
Mb =Pb SX = 116,646 x 2175 x 103 x 10-6 = 253,705 kN·m
Mb /MLT = 253,705 / 0,925 = 274,3 kNm
Portanto, MX = 90kNm
seção é suficiente
Desvio
A flecha máxima (δ) para uma viga simplesmente apoiada com distribuição uniforme pode ser calculada usando a seguinte equação.
δ = 5WtM4 / (384EI)
Esta equação pode ser ainda mais simplificada como segue.
δ = 0,104 MMáx.M2 / (EI)
Como avaliamos a deflexão com base nas cargas aplicadas, assumimos uma carga aplicada de 10 kN/m para este cálculo.
δ = 0,104 x 90 x 106 6.0002 / (205×103 x 478 x 106 ) = 1,7mm
Supondo que superfícies quebradiças sejam usadas
Envergadura / 360 = 6000/360 = 16,7 mm
δ < span / 360, portanto a deflexão está ok
Diferentes métodos para calcular distrações são explicados no artigo da Wikipedia distração (tecnologia).
Capacidade de carga da web
Ao projetar vigas de aço, a capacidade de carga da alma deve ser verificada. Nesta categoria são testadas a capacidade de carga da alma e a flambagem.
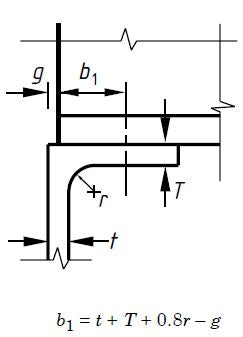
Pcara = (b1 + nk) tPSim
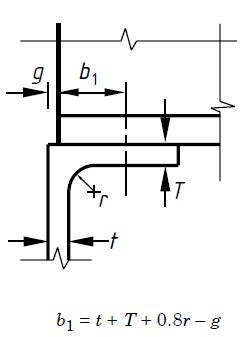
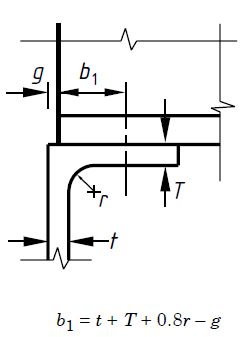
t = 10mm
T = 10mm
r = 10 mm
g = 5mm
bt = 5 mm
b1 = t + T + 0,8r – g = 10 + 10 + 0,8 x 10 – 5 = 23 mm
k = T + r = 16 + 20 = 36 mm (para perfil laminado)
no final,
n = (2 + 0,6bt/k) mas ≤ 5
n = (2 + 0,6 x 5/36) = 2,083 < 5 PSim = 275 N/mm2 da Tabela 9
Pcara = (b1 + nk) tPSim = (23 +2,083 x 36) x 10 x 275 x 10-3 = 269,5kN
A capacidade de carga é de 60 kN.
O rolamento da ponte está ok e não são necessários reforços.
Se FX >Pcara temos que fornecer reforços para reduzir as forças de compensação (FX -Pcara ). A capacidade de carga dos reforços é dada por PS = LIGADOs.net Pj. Onde ums.net é a área transversal de rigidez. Se a alma e a rigidez tiverem resistências diferentes, o valor menor deverá ser usado para calcular ambos P.S e Pcara.
Flambagem da ponte
Quando umt ≥ 0,7 dias
PX = 25εt Pcara /√( ( b1 + nk) d)
Quando umt <0,7 dias
PX = ( (umat +0,7d)/1,4d) {25εtPcara /√( (b1 + nk ) d ) }
Onde
At = 0,7d = 23/2 = 11,5 mm <0,7 x 428 = 300 mm
PX = ( (umat +0,7d)/1,4d) {25εtPcara /√( (b1 + nk ) d ) }
PX = ((11,5 +0,7×428)/1,4×428) {25x1x10x275 /√( (23 + 2,083×36) 428) } = 174,3 kN
FX
X
Não são necessários reforços.
A barra atende a todos os testes.