A seção super-reforçada é considerada crítica em comparação com o estado sub-reforçado. Se for reforçada demais, a seção pode falhar repentinamente e sem aviso devido à quebra do concreto.
Entretanto, sob condições de ganho insuficiente, a seção fornece um aviso mais forte de falha.
Portanto, o projetista deve ter um bom conhecimento destas condições, nomeadamente equilíbrio, sob condições reforçadas e sob condições reforçadas.
O artigo Equilíbrio, sobreamplificação e subamplificação Para obter mais informações sobre cada tipo e tipo de erro, você pode consultar.
Deve-se notar que as seções excessivamente reforçadas não falham repentinamente. Eles falham quando o momento aplicado excede a capacidade de momento. Se a seção falhar, não haverá avisos antes da falha, como seções com reforço insuficiente.
A avaliação do troço é realizada de acordo com as normas BS (BS 8110).
Este exemplo resolvido verifica o seguinte:
- A seção está superamplificada?
- Capacidade de momento fletor da seção sobrearmada?
Vamos verificar isso com um exemplo.
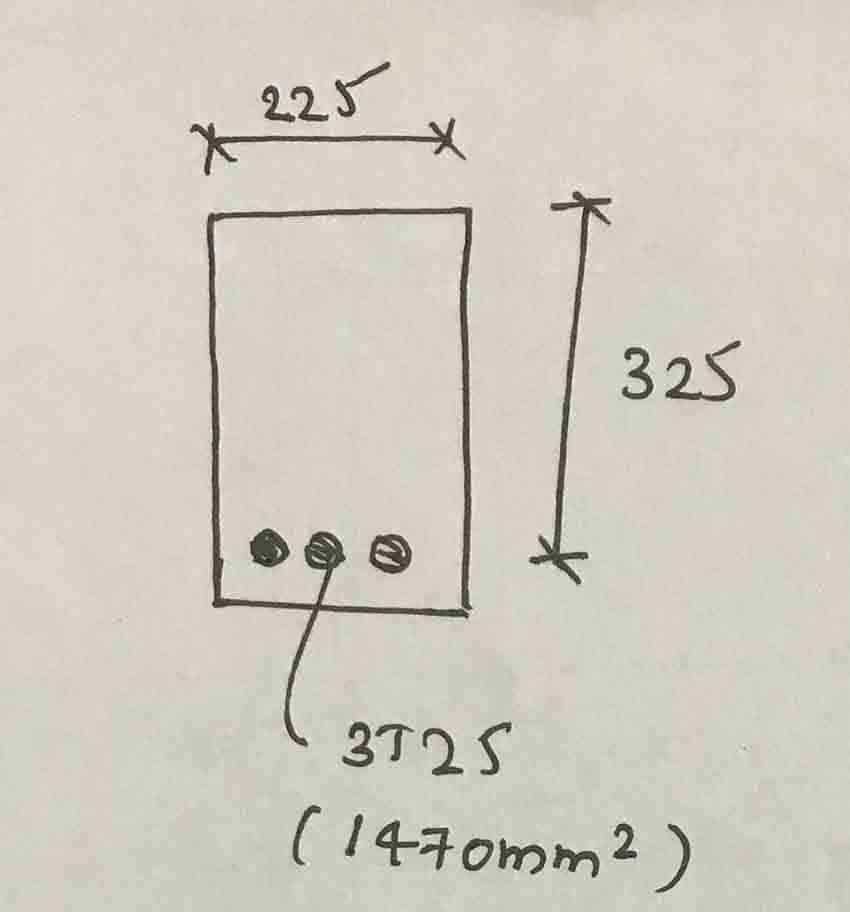
Observe a seção a seguir.
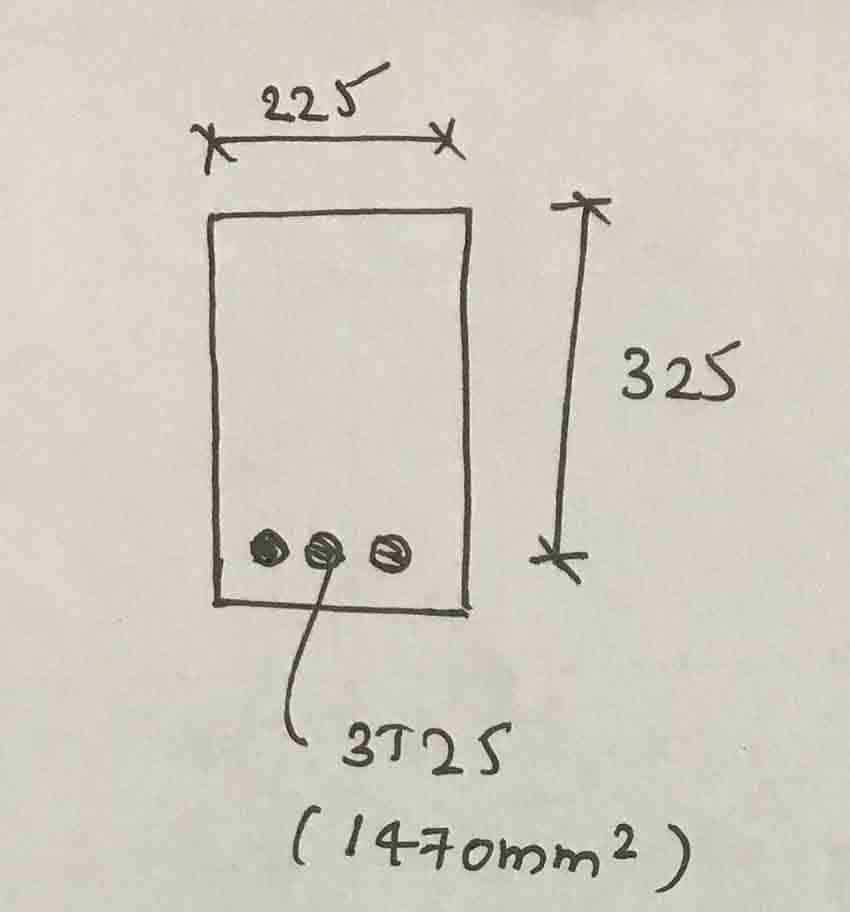

- Seção única reforçada
- Fcu = 25 N/mm2
- fy = 460 N/mm2
Neste cálculo levamos em consideração a relação tensão-deformação básica da seção transversal do concreto.
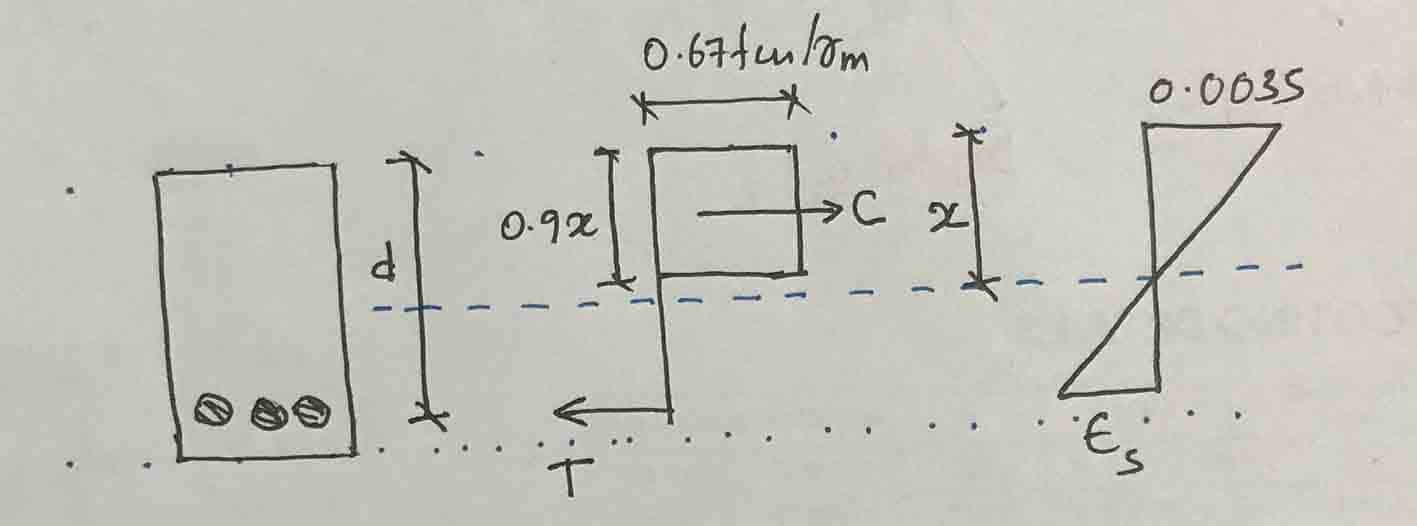
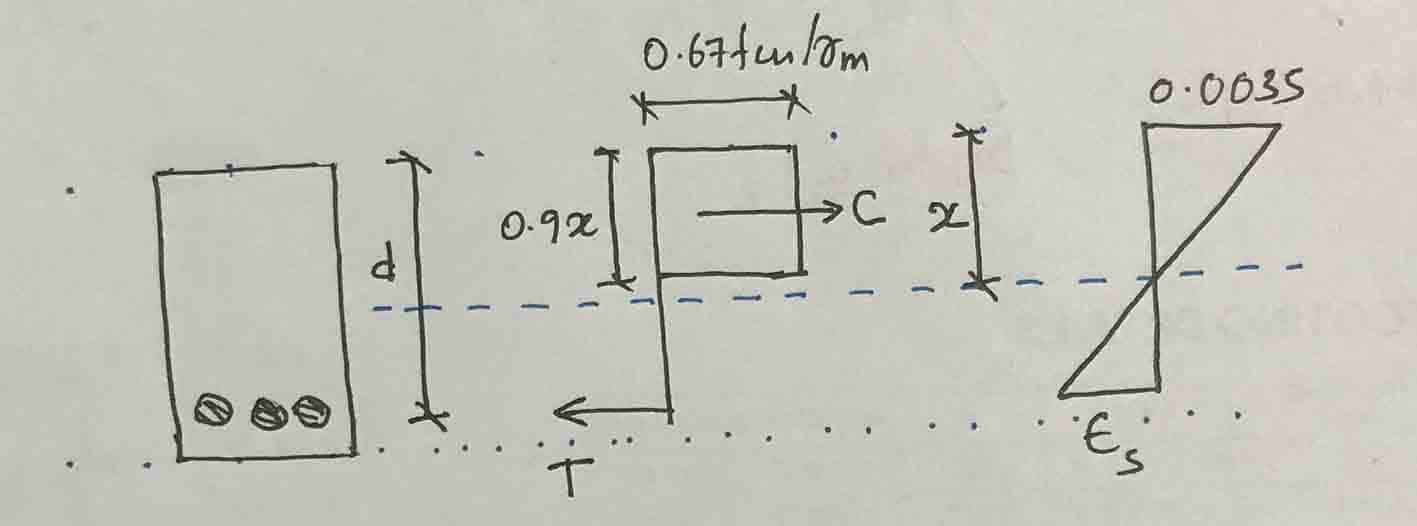
Vamos primeiro assumir Reforço é o retorno.
T = 0,87fjAS = 0,87 x 460 x 1470 = 588.294 N
C = (0,67fcu/ϒM)(0,9x)b = (0,67×25/1,5)(0,9x)x225 = 226,125X
C = T
226.125 X = 588.294
x = 260mm
x/d = 260/325 = 0,8 > 0,64
A seção é excessivamente reforçada.
A suposição de que o aço é durável está incorreta. Temos que descobrir o “x” real por tentativa e erro. Isso deve ser feito até C = T.
Suponha que x = 225 mm
C = 226125 X = 226125 x 225 = 508781,25N
Agora calcule a deformação do aço para encontrar a tensão do aço. A figura acima pode ser usada para calcular a deformação do aço.
εS = 0,0035(325-225)/225 = 0,0016
Agora vamos dar uma olhada no diagrama tensão-deformação.
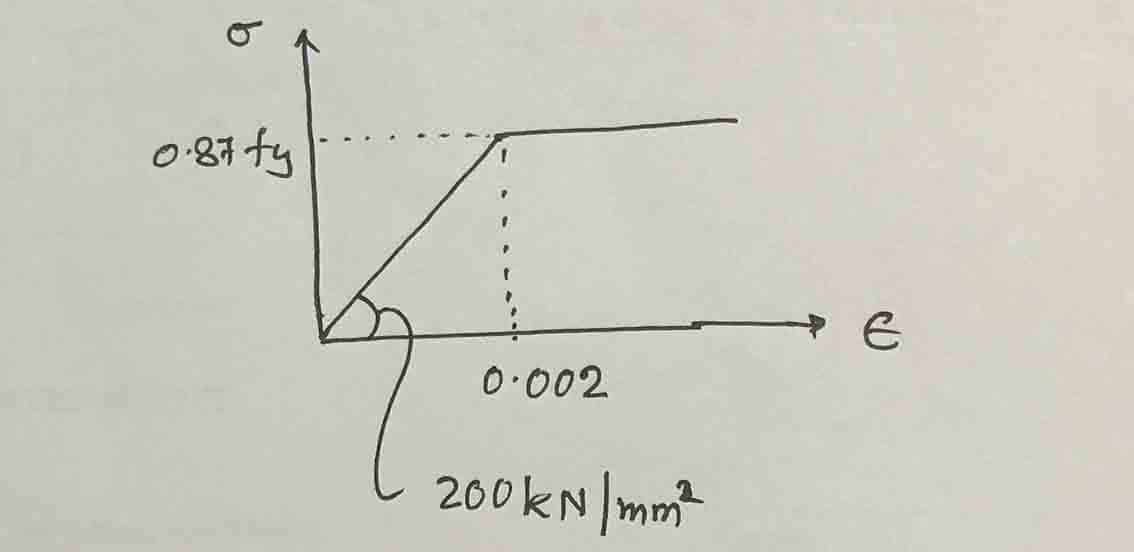
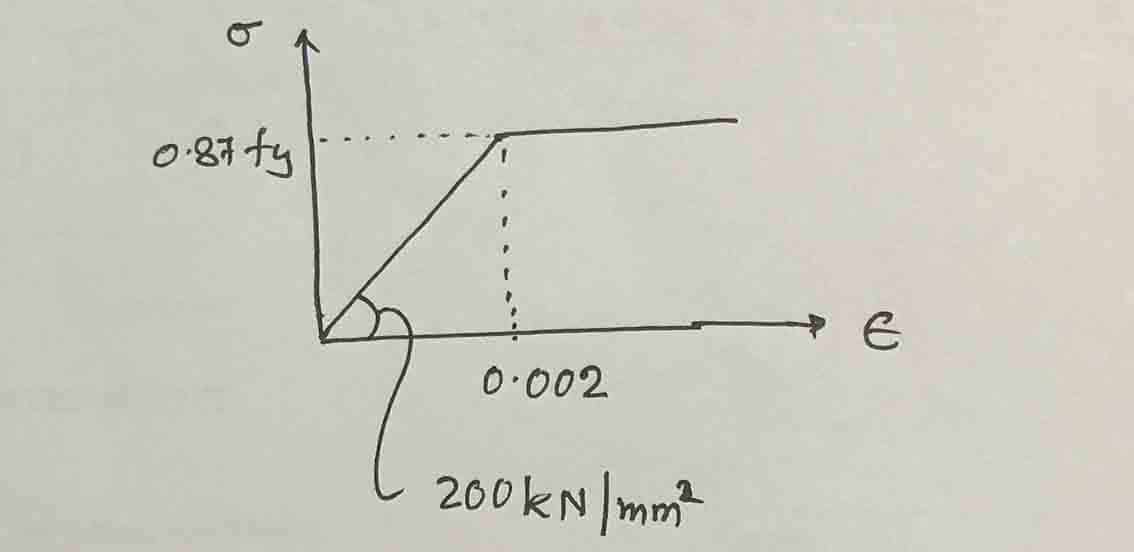
Tensão do aço, fS
FS = εS ES = 0,0016 x 200×103 = 320 N/mm2
T = 320 x 1470 = 470400N
C ≠ T
Precisamos realizar vários experimentos até C = T assumindo diferentes profundidades do eixo neutro (X).
Existe outro método para determinar diretamente a profundidade do eixo neutro. Como o aço não está abaixo do limite de escoamento (fs < 400 N/mm),2 = 0,87 × 460).
Calcule o alongamento do aço, εS
εS / 0,0035 = (d – x) / x
εS = 0,0035 (325 –x)/x
Agora calcule a tensão do aço
FS = εS ES = (0,0035 (325 – x)/x) 200×103
T=fS AS = (0,0035 (325 – x)/x) 200×103 x 1470
C = (0,67fcu/ϒM)(0,9x)b = (0,67×25/1,5)(0,9x)x225 = 2278,125X
T = C
(0,0035 (325 – x)/x) 200×103 x 1470 = 2278,125X
X2 + 451,69x – 146798,35 = 0
x = 218,91 ou -679,6; x deve ser positivo
Portanto x = 218,91 mm
Agora calcule a capacidade de flexão da seção
C = 2278,125 x 218,91 = 498704,34
Braço de alavanca
Z = d – 0,45x = 325 – 0,45 x 218,91 = 226,49 mm
M = Cz = 498704,34 x 226,49/10-6 = 112,95 kN·m
A capacidade de momento fletor da seção sobrearmada é de 112,95 kNm.
Você pode encontrar informações sobre isso no artigo da Wikipedia “Concreto armado”.