No tutorial anterior, foi discutida a minimização em nível de porta de funções booleanas. Uma função booleana deve ser expressa na forma padrão como soma de produtos (SoP) ou produto de somas (PoS). Uma vez que uma função booleana in case é minimizada para a forma SoP ou PoS, ela pode ser facilmente fabricada como uma implementação de dois níveis de portas AND e OR. Uma implementação de dois níveis é preferida para que haja um atraso mínimo na propagação do sinal através das portas lógicas, da entrada à saída do circuito digital.
Praticamente, os circuitos digitais são construídos com portas NAND ou NOR em vez de portas AND ou OR. As portas NAND e NOR são fáceis de fabricar com componentes semicondutores. Estas são as portas universais a partir das quais todas as outras portas lógicas podem ser construídas. É por isso que todos os ICs digitais são construídos com porta NAND ou NOR em vez de outras portas lógicas.
NAND como Portão Universal –
NAND é uma porta universal. Todas as outras portas lógicas podem ser construídas pela porta NAND. Uma porta NOT pode ser construída por uma porta NAND de uma entrada. Uma porta NAND de entrada única funciona da mesma forma que o inversor ou a porta NOT. A porta AND pode ser implementada conectando uma porta NAND a uma porta NAND de entrada única, onde a porta NAND de entrada única funcionará como inversor ou porta NOT. A porta OR pode ser implementada conectando entradas a portas NAND de entrada única atuando como inversor que então se conecta a uma porta NAND. A implementação das portas AND, OR e NOT com a ajuda da porta NAND é mostrada nos seguintes diagramas de portas lógicas –
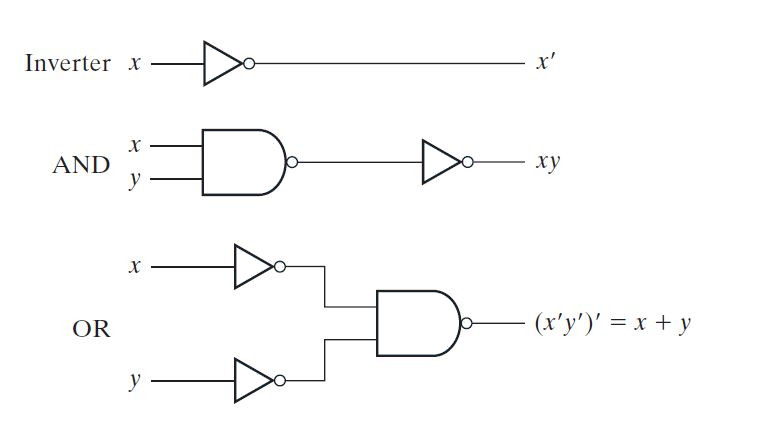
Fig. 1: Imagem mostrando a implementação de AND, OR e Invert com NAND Gate
Implementação de dois níveis com NAND Gate –
Para implementação em dois níveis de uma função booleana com porta NAND, ela deve ser expressa na forma de soma de produtos. A operação AND (produto) entre variáveis booleanas (caminhos de dados binários) pode ser implementada conectando as entradas a uma porta NAND que deve ser conectada a uma porta NAND de entrada única atuando como inversor. A operação OR (soma) pode ser implementada conectando as saídas do nível 1 a portas NAND de entrada única atuando como inversores que devem ser conectados a uma porta NAND. Como o complemento de um complemento de uma variável booleana é sua forma normal, as portas NAND de entrada única na saída do nível 1 e na entrada do nível 2 nas mesmas linhas podem ser removidas. Portanto, uma expressão de soma de produto pode ser implementada por portas NAND por meio de uma simples implementação NAND-NAND.
Suponha que uma função booleana de quatro variáveis F seja a seguinte –
F = AB + CD
Na implementação AND-OR, seu diagrama de porta lógica será o seguinte –
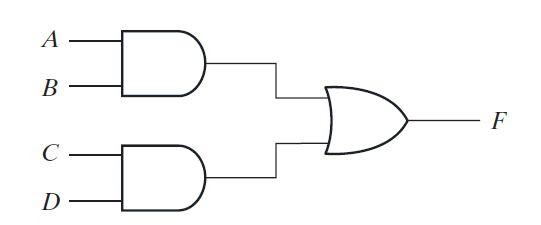
Fig. 2: Imagem mostrando a implementação AND-OR de dois níveis antes da implementação NAND-NAND
Uma porta NAND pode ser mostrada como AND-Invert ou Invert-OR, pois são equivalentes. Os seguintes símbolos gráficos podem ser usados para porta NAND –
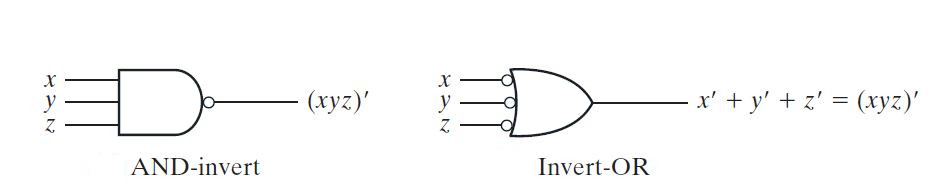
Fig. 3: Símbolos da porta NAND
Ao substituir a porta AND mais OR pela porta NAND na implementação da função F, obtém-se o seguinte diagrama lógico –
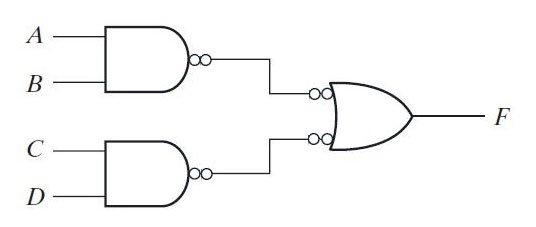
Fig. 4: Imagem mostrando a substituição das portas AND-OR pela porta NAND
Como mencionado acima, o complemento de um complemento de uma variável booleana é sua forma normal, as portas NAND de entrada única na saída do nível 1 e na entrada do nível 2 nas mesmas linhas podem ser removidas. Portanto, após remover um número par de inversores na mesma linha, a implementação NAND-NAND final da função será a seguinte –
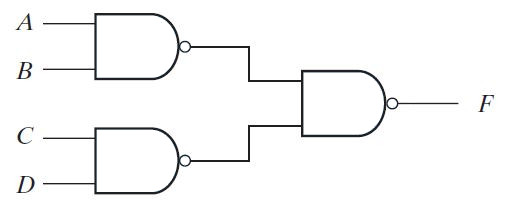
Fig. 5: Imagem mostrando a implementação NAND-NAND de dois níveis de uma expressão de soma de produto
Implementação multinível com NAND Gate –
A estrutura de gating de um circuito digital nem sempre precisa ser viável para ser implementada em dois níveis. Muitas vezes, devido a limitações de projeto ou para viabilidade de fabricação de um CI, pode ser necessária a implementação do diagrama de portas lógicas de um circuito digital em três ou quatro níveis. aqui estão também algumas funções booleanas como Ex-OR, que só podem ser implementadas em estruturas de portas de 3 níveis ou mais. Nesse caso, a função booleana deve primeiro ser expressa em termos de portas AND, OR e NOT. Um diagrama de portas lógicas com portas AND, OR e NOT deve ser desenhado e as portas AND, OR e NOT devem ser substituídas por seus equivalentes NAND. Agora, o número par de bolhas (denotando NOT na porta NAND) nas mesmas linhas deve ser removido e as bolhas únicas restantes nas linhas devem ser substituídas por portas NAND de entrada única. A esquerda está o diagrama da porta lógica totalmente NAND do circuito digital.
NOR como Portão Universal –
NOR também é uma porta universal como a porta NAND. Todas as outras portas lógicas também podem ser construídas pela porta NOR. Uma porta NOT pode ser construída por uma porta NOR de uma entrada. Uma porta NOR de entrada única funciona da mesma forma que o inversor ou a porta NOT. A porta OR pode ser implementada conectando uma porta NOR a uma porta NOR de entrada única, onde a porta NOR de entrada única funcionará como inversor ou porta NOT. A porta AND pode ser implementada conectando entradas a portas NOR de entrada única atuando como inversor que então se conecta a uma porta NOR. A implementação de outras portas com porta NOR é o duplo da implementação de outras portas com porta NAND. A implementação das portas AND, OR e NOT com a ajuda da porta NOR é mostrada nos seguintes diagramas de portas lógicas –
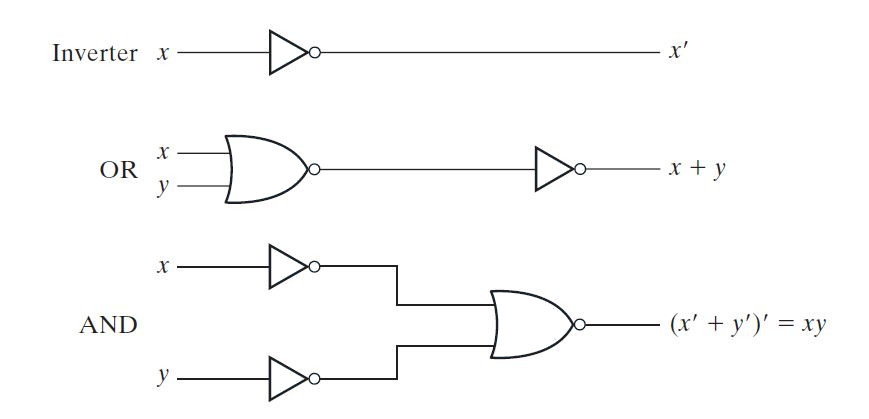
Fig. 6: Imagem mostrando a implementação de AND, OR e Invert com porta NOR
Implementação de dois níveis com NOR Gate –
Para implementação em dois níveis de uma função booleana com porta NOR, ela deve ser expressa na forma de produto de somas. A implementação da porta NOR da porta AND, OR e NOT é apenas o dual da implementação da porta NAND. A operação OR (soma) entre variáveis booleanas (caminhos de dados binários) pode ser implementada conectando as entradas a uma porta NOR que deve ser conectada a uma porta NOR de entrada única atuando como inversor. A operação AND (produto) pode ser implementada conectando as saídas do nível 1 a portas NOR de entrada única atuando como inversores que devem ser conectados a outra porta NOR. Como o complemento de um complemento de uma variável booleana é sua forma normal, as portas NOR de entrada única na saída do nível 1 e na entrada do nível 2 nas mesmas linhas podem ser removidas. Portanto, uma expressão de produto de soma pode ser implementada por portas NOR por meio de uma simples implementação NOR-NOR.
Suponha que uma função booleana de quatro variáveis F seja a seguinte –
F = (A + B)(C + D)
Na implementação AND-OR, seu diagrama de porta lógica será o seguinte –
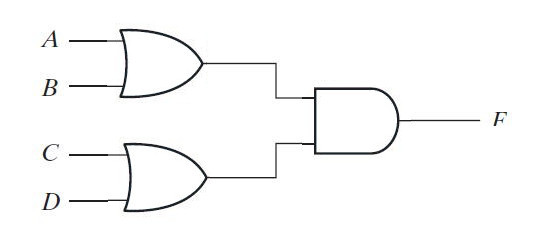
Fig. 7: Imagem mostrando a implementação AND-OR de dois níveis antes da implementação NOR-NOR
Uma porta NOR pode ser mostrada como OR-Invert ou Invert-AND, pois são equivalentes. Os seguintes símbolos gráficos podem ser usados para porta NOR –

Fig. 8: Símbolos da porta NOR
Ao substituir as portas AND, OR e NOT pela porta NOR na implementação da função F, obtém-se o seguinte diagrama lógico –
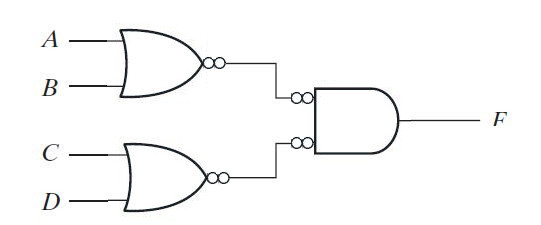
Fig. 9: Imagem mostrando a substituição das portas AND-OR pela porta NOR
Como mencionado acima, o complemento de um complemento de uma variável booleana é sua forma normal, as portas NOR de entrada única na saída do nível 1 e na entrada do nível 2 nas mesmas linhas podem ser removidas. Assim, após remover um número par de inversores na mesma linha, a implementação NOR-NOR final da função será a seguinte –
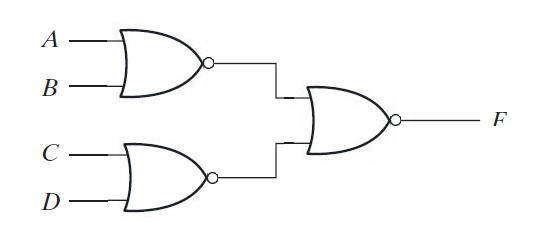
Fig. 10: Imagem mostrando a implementação NOR-NOR de dois níveis de um produto de expressão de soma
Todas as possíveis implementações de dois níveis e formas não degeneradas –
Considerando a implementação de funções booleanas em dois níveis e tendo as portas AND, OR, NAND e NOR disponíveis, pode haver dezesseis combinações possíveis para implementação em dois níveis de uma expressão booleana. As oito dessas combinações degeneram em operação única, por isso são chamadas de formas degeneradas. As oito formas degeneradas são as seguintes –
1) E E: Degenera para operação AND. Como se houvesse quatro variáveis booleanas A, B, C e D conectadas na estrutura da porta AND-AND, será deduzido como segue –
F = (AB)(CD)
= ABCD
2) E-NAND: Degenera para operação NAND. Como se houvesse quatro variáveis booleanas A, B, C e D conectadas na estrutura da porta AND-NAND, será deduzido como segue –
F = ((AB)(CD))'
= (AB)' + (CD)'
= A' + B' + C' + D'
= (ABCD)'
3) OU OU: Degenera para operação OR. Como se houvesse quatro variáveis booleanas A, B, C e D conectadas na estrutura da porta OR-OR, será deduzido como segue –
F = (A + B) + (C + D)
= A + B + C + D
4) OU-NOR: Degenera para operação NOR. Como se houvesse quatro variáveis booleanas A, B, C e D conectadas na estrutura da porta OR-NOR, será deduzido como segue –
F = ((A + B) + (C + D))'
= (A + B)'(C + D)'
=A'B'C'D'
= (A + B + C + D)'
5) NAND-OU: Degenera para operação NAND. Como se houvesse quatro variáveis booleanas A, B, C e D conectadas na estrutura da porta NAND-OR, será deduzido como segue –
F = (AB)' + (CD)'
= A' + B' + C' + D'
= (ABCD)'
6) NAND-NOR: Degenera para operação AND. Como se houvesse quatro variáveis booleanas A, B, C e D conectadas na estrutura da porta NAND-NOR, será deduzido como segue –
F = ((AB)' + (CD)')'
= (A' + B' + C' + D')'
= (ABCD)
7) NEM-E: Degenera para operação NOR. Como se houvesse quatro variáveis booleanas A, B, C e D conectadas na estrutura da porta NOR-AND, será deduzido como segue –
F = (A + B)'(C + D)'
=A'B'C'D'
= (A + B + C + D)'
8) NOR-NAND: degenera para operação OR. Como se houvesse quatro variáveis booleanas A, B, C e D conectadas na estrutura da porta NOR-NAND, será deduzido como segue –
F = ((A + B)'(C + D)')'
= (A + B) + (C + D)
= A + B + C + D
As oito formas restantes deduzem a expressão da soma dos produtos ou a expressão do produto da soma para uma função booleana. Estas são chamadas de formas não degeneradas. As oito formas não degeneradas são AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NAND-NAND, NOR-OR e NOR-NOR. O AND-OR é dual de OR-AND, NAND-NAND é dual de NOR-NOR, NOR-OR é dual de NAND-AND enquanto OR-NAND é dual de AND-NOR e vice-versa. As formas AND-OR e OR-AND são formas básicas de uma expressão booleana. Os formulários NAND-NAND e NOR-NOR são a implementação universal de qualquer função booleana. O NAND-AND e AND-NOR são equivalentes e chamados de implementação AND-OR-Invert. O OR-AND e o NOR-OR também são equivalentes e chamados de implementação OR-AND-Invert.
Implementação AND-OU-Inverter –
Tanto NAND-AND quanto AND-NOR executam a operação AND-OR-Invert. É uma operação AND-OR simples com operação invertida implementada na saída. Suponha que existam quatro variáveis booleanas – A, B, C e D, então a operação NAND-AND entre elas será a seguinte –
F = (AB)'(CD)'
= (AB + CD)'
Da mesma forma, a operação AND-NOR com quatro variáveis booleanas – A, B, C e D será deduzida da seguinte forma –
F = (AB+CD)'
Implementação OR-AND-Invert –
Tanto OR-NAND quanto NOR-OR executam a operação OR-AND-Invert. É uma operação OR-AND simples com operação invertida implementada na saída. Suponha que existam quatro variáveis booleanas – A, B, C e D, então a operação OR-NAND entre elas será a seguinte –
F = ((A + B)(C + D))'
Da mesma forma, a operação NOR-OR com quatro variáveis booleanas – A, B, C e D será deduzida como segue –
F = (A + B)' + (C + D)'
= ((A + B)(C + D))'
Agora, com o conhecimento da implementação em nível de porta, qualquer função booleana pode ser construída com portas lógicas universais – NAND e NOR. No próximo tutorial, há um breve introdução ao VHDL. VHDL é uma linguagem baseada em computador que descreve o hardware de um circuito digital em forma textual. É uma ferramenta de projeto baseada em computador extremamente útil no projeto de circuitos digitais de grande escala. O projeto de pequenos circuitos pode ser feito manualmente, mas grandes circuitos digitais requerem ferramentas computacionais para serem projetados. Essas ferramentas não apenas facilitam o processo de design, mas também reduzem as chances de um design falho.

