No primeiro tutorial desta série – Introdução à Eletrônica Digital, foi mencionado que existem diferentes sistemas de códigos que são usados para representar informações digitais como números binários. Cada sistema de código possui diferentes números binários atribuídos aos mesmos símbolos e caracteres. Os diferentes sistemas digitais podem utilizar diferentes sistemas de códigos. Nesse caso, deve permanecer algum circuito de conversão de código para tornar compatíveis os sistemas digitais interligados.
Neste tutorial, os circuitos de conversão de código serão projetados usando a série SN7400 de ICs digitais. No tutorial anterior, a mesma série de CIs digitais foi usada para construir circuitos aritméticos como meio somador, somador completo, meio subtrator e subtrator completo. Neste tutorial, os seguintes circuitos de conversão de código serão projetados –
· Conversor de código binário para Gray
· Conversor de código cinza para binário
· BCD em excesso – conversor de 3 códigos
· Excesso – conversor de código 3 para BCD
Os circuitos de conversão de código projetados neste tutorial serão usados para conversão dos dígitos 0 a 9 de um sistema de código para outro. Os diferentes sistemas de código possuem diferentes números binários atribuídos aos dígitos. Como no código cinza, os números binários são ordenados de tal forma que quaisquer dois dígitos ou valores sucessivos diferem apenas em um bit. O sistema de numeração BCD é semelhante à representação binária dos números decimais, exceto que o número codificado é separado em quatro bits para cada dígito do número decimal. Portanto, o número codificado é representado por valores binários ponderados onde cada valor tem 4 bits de comprimento e é uma representação direta dos dígitos do número decimal. O código Excess-3 é semelhante ao sistema de numeração BCD, com a única diferença de que cada valor longo de 4 bits no número codificado é obtido adicionando 3 à representação BCD. A tabela a seguir resume a representação binária dos dígitos de 0 a 9 em diferentes sistemas de código –
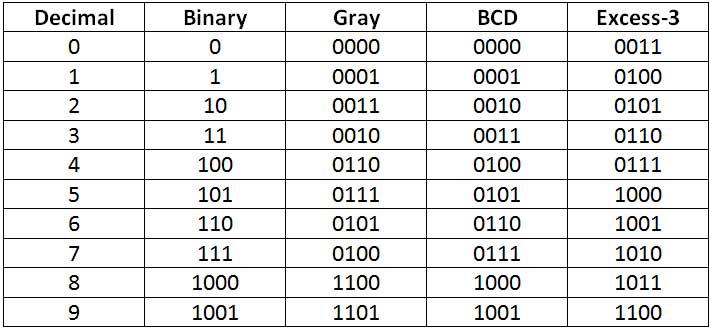
Fig. 1: Tabela listando codificação binária, cinza, BCD e Express-3 para dígitos decimais
Com o conhecimento desses sistemas de código, vamos agora começar a construir os circuitos conversores de código.
Componentes necessários –

Fig. 2: Lista de componentes necessários para fazer conversores de código baseados em IC da série SN-7400
Diagramas de Circuito –
O conversor de código binário para cinza tem o seguinte diagrama de circuito –

Fig. 3: Diagrama de Circuito do Conversor de Código Binário para Gray
O conversor de código cinza para binário tem o seguinte diagrama de circuito –

Fig. 4: Diagrama de circuito do conversor de código cinza para binário
O conversor de código BCD para excesso – 3 possui o seguinte diagrama de circuito –
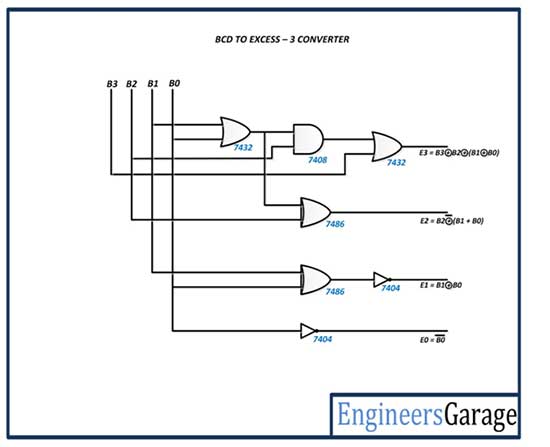
Fig. 5: Diagrama de Circuito do Conversor BCD para Excesso 3
O conversor de código Excesso – 3 para BCD tem o seguinte diagrama de circuito –

Fig. 6: Circuito Combinacional do Conversor de Código Excesso 3 para BCD
Conexões de Circuito –
Os circuitos conversores de código projetados neste tutorial são circuitos combinacionais, pois sua saída depende apenas dos valores de entrada atuais. Cada circuito possui uma tabela verdade única a partir da qual a respectiva expressão booleana para cada saída pode ser derivada. A expressão booleana minimizada é então convertida em um diagrama de porta lógica que é construído em uma placa de ensaio usando ICs da série 7400.
Os seguintes ICs de porta lógica são usados na construção dos circuitos –
7408 IC – O 7408 IC possui portas AND quádruplas de 2 entradas. O IC tem a seguinte configuração de pinos –
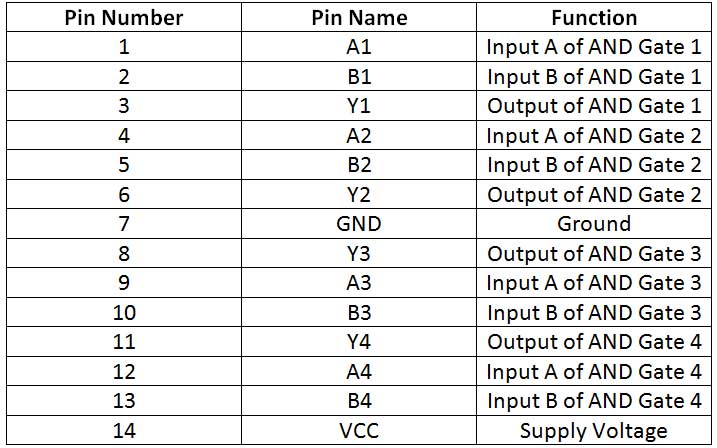
Fig. 7: Diagrama de Circuito do Conversor de Excesso 3 para Código BCD
O IC tem o seguinte diagrama de pinos –
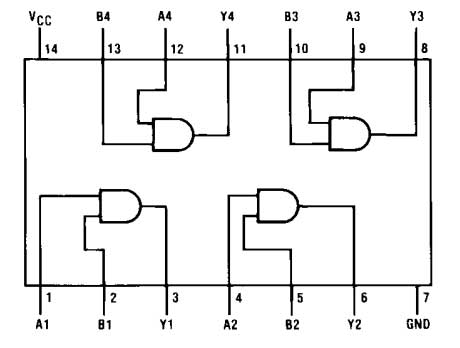
Fig. 8: Diagrama de pinos do 7408 IC
O IC requer uma tensão de alimentação de 5V que pode ser tolerada até 7V. A tensão nas entradas das portas AND deve ser 2V para lógica alta e 0V para lógica baixa. A saída das portas AND possui uma tensão de 3,4 V para lógica alta e 0,2 V para lógica baixa. O IC opera em sistema lógico positivo. O atraso de propagação durante o trânsito do nível BAIXO para o ALTO na saída é de 27 ns, enquanto o atraso de propagação durante o trânsito do nível ALTO para o BAIXO na saída é de 19 ns.
7432 IC – O 7432 IC possui portas OR quádruplas de 2 entradas. O IC tem a seguinte configuração de pinos –

Fig. 9: Tabela listando a configuração dos pinos do 7432 IC
O IC tem o seguinte diagrama de pinos –

Fig. 10: Diagrama de pinos do 7432 IC
O IC requer uma tensão de alimentação de 5V que pode ser tolerada até 7V. A tensão nas entradas das portas OR deve ser 2V para lógica alta e 0V para lógica baixa. A saída das portas OR possui tensão de 3,4 V para lógica alta e 0,35 V para lógica baixa. O IC opera em sistema lógico positivo. O atraso de propagação durante o trânsito do nível BAIXO para o ALTO na saída é de 3 a 15 ns, enquanto o atraso de propagação durante o trânsito do nível ALTO para o BAIXO na saída também é de 3 a 15 ns.
7486 CI – O IC 7486 possui portas EX-OR quádruplas de 2 entradas. O IC tem a seguinte configuração de pinos –

Fig. 11: Tabela listando a configuração dos pinos do 7486 IC
O IC tem o seguinte diagrama de pinos –
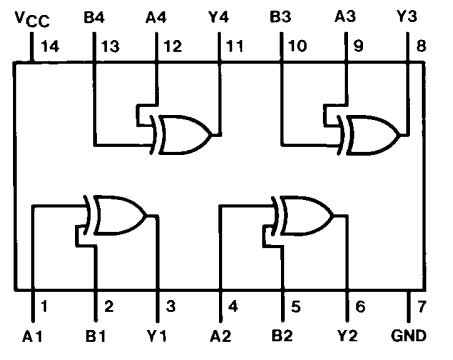
Fig. 12: Diagrama de pinos do 7486 IC
O IC requer uma tensão de alimentação de 5V que pode ser tolerada até 7V. A tensão nas entradas das portas EX-OR deve ser 2V para lógica alta e 0V para lógica baixa. A saída das portas EX-OR possui tensão de 3,4 V para lógica alta e 0,2 V para lógica baixa. O IC opera em sistema lógico positivo. O atraso de propagação durante a transição do nível BAIXO para o nível ALTO na saída é de 23 ns se outras entradas forem baixas e 30 ns se outras entradas forem altas, enquanto o atraso de propagação durante a transição do nível ALTO para o nível BAIXO na saída é de 17 ns se outras entradas forem baixas e 22 ns se outras entradas forem altas.
7404 CI – O IC 7404 possui seis portas inversoras. O IC tem a seguinte configuração de pinos –

Fig. 13: Tabela listando a configuração dos pinos do 7404 IC
O IC tem o seguinte diagrama de pinos –

Fig. 14: Diagrama de pinos do 7404 IC
O IC requer uma tensão de alimentação de 5V que pode ser tolerada até 7V. A tensão nas entradas das portas NOT deve ser de 2 V para lógica alta e 0,8 V para lógica baixa. A saída das portas NOT ter uma tensão de 3,4 V para lógica alta e 0,2 V para lógica baixa. O IC opera em positivo sistema lógico. O atraso de propagação durante o trânsito de LOW para ALTO O nível na saída é de 22 ns, enquanto o atraso de propagação durante o trânsito de ALTO para BAIXO o nível na saída é de 15 ns.
Deve-se observar que os CIs selecionados possuem níveis de tensão de entrada, saída e alimentação compatíveis, pois são retirados de uma família comum (série 74XX) de CIs digitais.
Como funciona o circuito –
Existem diferentes sistemas de código disponíveis para representação de informação digital. Muitas vezes, os sistemas digitais utilizam componentes que podem utilizar sistemas de códigos diferentes. Neste caso, deve haver algum circuito conversor de código entre tais componentes, para que possam comunicar informações digitais entre eles. Os sistemas de código comumente usados incluem código Gray, BCD e Excess-3. Em todos esses sistemas de código, cada dígito binário é representado por um valor exclusivo de 4 bits. Por conveniência, a entrada binária no conversor de código binário para cinza e a saída binária no conversor de código cinza para binário também têm 4 bits de comprimento.
Assim, como cada código usa quatro bits para representar um dígito decimal, existem quatro entradas e quatro saídas. Deve-se notar que o código Gray é um código não ponderado, enquanto BCD e Excess-3 são sistemas de código ponderado. Nos conversores de código BCD e Excess-3, o circuito é projetado apenas para conversão de um único dígito. As variáveis de entrada são designadas como B3, B2, B1, B0 e as variáveis de saída são designadas como G3, G2, G1, G0. A partir da tabela verdade, são obtidos os K-maps para cada uma das quatro saídas dos respectivos circuitos e são derivadas funções booleanas envolvendo quatro variáveis de entrada para cada variável de saída. Um diagrama lógico de dois níveis é obtido diretamente das expressões booleanas derivadas dos mapas e circuitos combinacionais são projetados para cada variável nos respectivos circuitos.
Conversor de código binário para cinza –
Os números binários são representações não ponderadas de números decimais na base 2. O código cinza que também é chamado de Código Binário Refletido (RBC) ou apenas Binário Refletido (RB) possui números binários ordenados para os dígitos decimais de tal forma que quaisquer dois sucessivos os valores diferem apenas em um bit. O código cinza é amplamente utilizado em sistemas de comunicação digital para correção de erros. Os números binários de entrada aqui são considerados como tendo 4 bits de comprimento. Para derivar o código cinza equivalente aos números binários, primeiro o MSB (Bit Mais Significativo) é anotado como está, então cada dígito inferior no número do código cinza é obtido adicionando o respectivo bit e o bit uma posição inferior no número binário . O circuito possui quatro entradas (B3 B2 B1 B0) representando números binários de 4 bits e quatro saídas (G3 G2 G1 G0) representando o código cinza de 4 bits. O circuito conversor tem a seguinte tabela verdade –

Fig. 15: Tabela Verdade do Conversor de Código Binário para Gray
A partir da tabela verdade acima, são obtidos os seguintes K-Maps para as variáveis de saída –

Fig. 16: K-Map para G3 no conversor de código binário para cinza
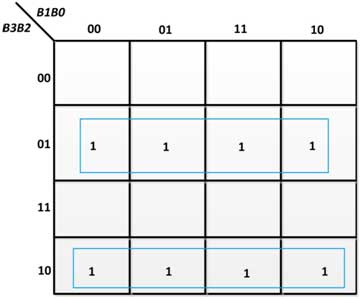
Fig. 17: K-Map para G2 no conversor de código binário para cinza

Fig. 18: K-Map para G1 no conversor de código binário para cinza
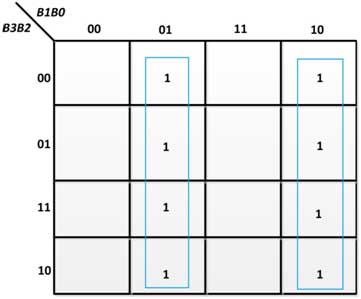
Fig. 19: K-Map para G0 no conversor de código binário para cinza
A partir dos K-maps acima, as seguintes expressões booleanas são obtidas para as variáveis de saída –
G3 = B3
G2 = B3  B2
B2
G1 = B2  B1
B1
G0 = B1  B0
B0
Portanto, o circuito digital do conversor de código binário para cinza usa portas EX-OR. Ele pode ser construído usando 7486 IC.
Conversor de código Gray para binário
Para conversão do código cinza em binário, o MSB é escrito como está e os bits subsequentes são obtidos adicionando MSB (ou bit de posição superior no número binário convertido) e o respectivo bit no número com código cinza. O circuito tem quatro entradas (G3 G2 G1 G0) representando código cinza de 4 bits e quatro saídas (B3 B2 B1 B0) representando números binários de 4 bits. O circuito conversor tem a seguinte tabela verdade –
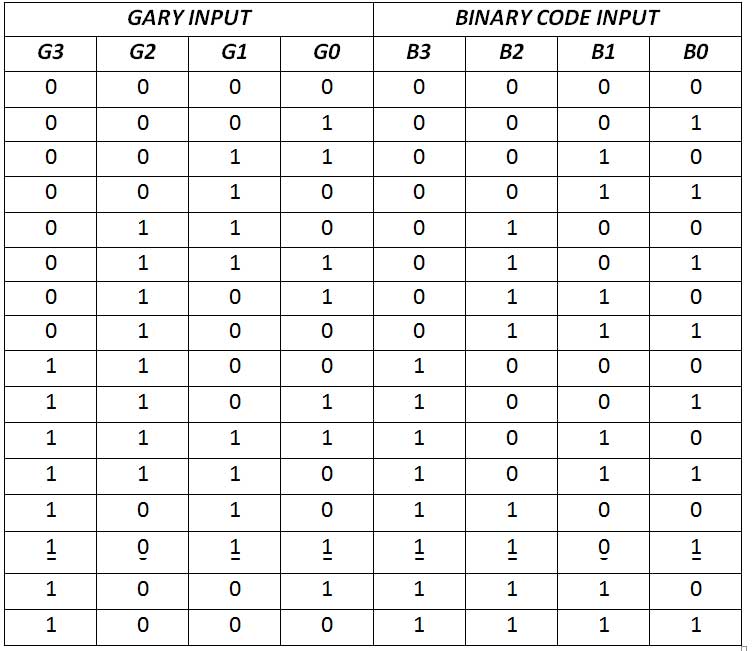
Fig. 20: Tabela Verdade do Conversor de Código Gray para Binário
A partir da tabela verdade acima, são obtidos os seguintes K-Maps para as variáveis de saída –

Fig. 21: K-Map para B3 em conversor de código cinza para binário

Figura 22: K-Map para B2 em conversor de código cinza para binário

Figura 23: K-Map para B1 em conversor de código cinza para binário

Figura 24: K-Map para B0 em conversor de código cinza para binário
A partir dos K-maps acima, as seguintes expressões booleanas são obtidas para as variáveis de saída –
B3 = G3
B2 = G3  G2
G2
B1 = G3  G2
G2  G1
G1
B0 = G3  G2
G2  G1
G1  G0
G0
Portanto, o circuito digital do conversor de código cinza para binário usa portas EX-OR. Ele pode ser construído usando 7486 IC.
Conversor BCD para Excesso-3
Os números BCD de 4 bits são iguais aos números binários de 4 bits. Os números codificados em excesso 3 são adicionados 3 a cada número BCD. Tanto o BCD quanto o Excess-3 são sistemas de código ponderado. O circuito projetado aqui converte apenas números BCD de um dígito em números Excess-3 equivalentes de um dígito. O circuito tem quatro entradas (B3 B2 B1 B0) representando código BCD de 4 bits e quatro saídas (E3 E2 E1 E0) representando excesso de 4 bits – 3 números. O circuito conversor tem a seguinte tabela verdade –

Fig. 25: Tabela Verdade do Conversor BCD para Excesso-3
A partir da tabela verdade acima, são obtidos os seguintes K-Maps para as variáveis de saída –
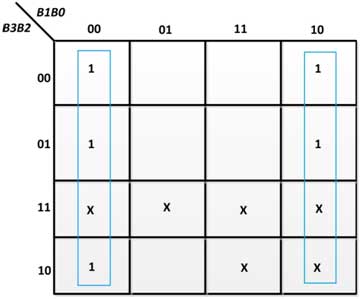
Figura 26: K-Map para E0 no conversor de código BCD para excesso-3

Figura 27: K-Map para E1 no conversor de código BCD para excesso-3

Figura 28: K-Map para E2 em conversor de código BCD para excesso-3
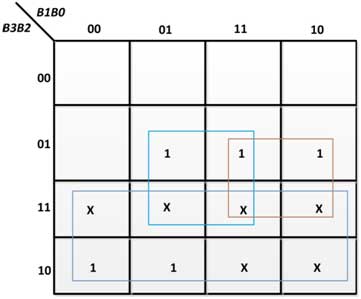
Figura 29: K-Map para E3 em conversor de código BCD para excesso-3
A partir dos K-maps acima, as seguintes expressões booleanas são obtidas para as variáveis de saída –
E0 = B0'
E1 =B1  B0
B0
E2 = B2  (B1 + B0)
(B1 + B0)
E3 = B3  B2
B2  (B1
(B1  B0)
B0)
Portanto, o circuito digital do conversor de código BCD para excesso 3 usa portas EX-OR, AND e NOT. Ele pode ser construído usando ICs 7486, 7432, 7408 e 7404.
Conversor Excesso-3 para BCD
Os números codificados BCD são três a menos que os números codificados em Excesso-3. O circuito conversor possui quatro entradas (X3 X2 X1 X0) representando excesso de 4 bits – 3 códigos e quatro saídas (ABCD) representando números BCD de 4 bits. Tem a seguinte tabela verdade –
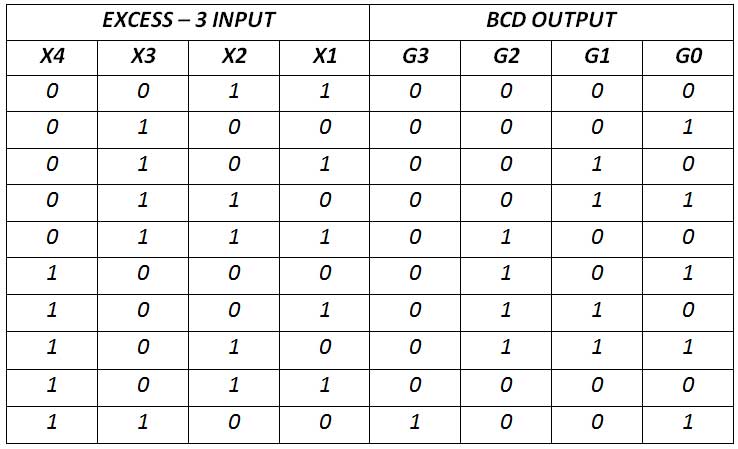
Fig. 30: Tabela Verdade do Conversor de Excesso-3 para Código BCD
A partir da tabela verdade acima, são obtidos os seguintes K-Maps para as variáveis de saída –

Figura 31: K-Map para A em excesso-3 para conversor de código BCD
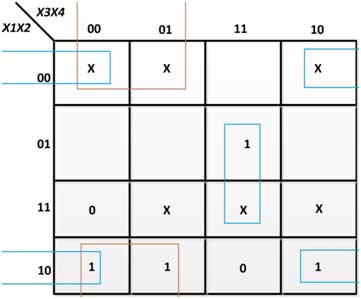
Figura 32: K-Map para B em excesso-3 para conversor de código BCD

Figura 33: K-Map para C em excesso-3 para conversor de código BCD
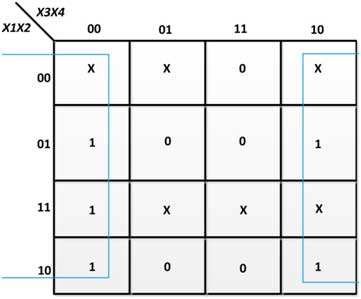
Figura 34: K-Map para D em excesso-3 para conversor de código BCD
A partir dos K-maps acima, as seguintes expressões booleanas são obtidas para as variáveis de saída –
UMA = X1(X2 + X3.X4)
B = X2  (X3′ + X4′)
(X3′ + X4′)
C = X3  X4
X4
D = X4′
Portanto, o circuito digital para o conversor de código em excesso para BCD usa portas EX-OR, AND e NOT. Ele pode ser construído usando ICs 7486, 7432, 7408 e 7404.
Testando os circuitos –
Os circuitos projetados acima podem ser testados fornecendo tensão de alimentação aos ICs por uma bateria por meio do regulador de tensão 7805. A mesma tensão pode ser reduzida para o nível de 2 V usando um resistor variável para lógica ALTA enquanto fornece lógica BAIXA através do terra. Os sinais de saída podem ser verificados conectando LEDs nos pinos de saída de cada circuito conversor. Os circuitos podem ser verificados verificando as tabelas verdade de cada circuito.
No próximo tutorial, aprenda a projetar um comparador de magnitude de bits.
Diagramas de circuito
| Diagrama de Circuito-BCD-Excesso-3-Conversor |  |
| Circuito-Diagrama-Excesso-Conversor de Código BCD |  |

