Os tutoriais anteriores lançaram as bases para a síntese lógica e o projeto de circuitos digitais. Os circuitos digitais em geral sempre têm aplicação como dispositivos de computação, seja como processador, controlador ou CIs específicos de aplicação. Como dispositivo de computação, o circuito digital de um processador, controlador ou ASIC deve ser essencialmente capaz de realizar operações aritméticas. A implementação de operações aritméticas por circuitos digitais é ainda usada para construir lógicas de computação complexas e funções matemáticas.
Em um processador/controlador/ASIC, as operações aritméticas em números binários inteiros são realizadas pela Unidade Lógica Aritmética (ALU), enquanto as operações aritméticas em números de ponto flutuante são realizadas pela Unidade de Ponto Flutuante (FPU). A própria unidade de ponto flutuante é construída a partir de várias ALUs. Dentro de uma Unidade Central de Processamento (CPU) ou Unidade de Processamento Gráfico (GPU) de um computador/dispositivo de computação, existem muitas ALU e/ou FPU (onde as próprias FPU são construídas a partir de múltiplas ALU).
Os circuitos digitais podem ser de dois tipos – 1) Circuitos Lógicos Combinacionais ou 2) Circuitos Lógicos Sequenciais. Num circuito combinacional, a saída do circuito depende apenas dos valores de entrada naquele momento. Em circuitos sequenciais, a saída depende não apenas da entrada atual, mas também dos valores de saída anteriores. As ALU são construídas por circuitos combinacionais. A ALU normalmente é projetada para realizar as seguintes operações:
1) Operaçoes aritimeticas – Geralmente, as operações aritméticas suportadas pela ALU são adição, adição com transporte, subtração, subtração com empréstimo, complemento de dois, incremento, decremento e passagem.
2) Operações lógicas bit a bit – As operações lógicas suportadas pela ALU são AND, OR, Exclusive-OR e One's Complement.
3) Operações de mudança de bits – As operações de deslocamento de bits implementadas em uma ALU incluem deslocamento aritmético, deslocamento lógico, rotação e rotação através de transporte.
Portanto, a ALU pode realizar operações aritméticas como adição e subtração e, portanto, multiplicação e divisão em números binários inteiros. Um número binário pode estar disponível para a ALU de um processador digital como entrada paralela de 8 bits, 16 bits, 32 bits ou 64 bits, dependendo se for de 8 bits, 16 bits, 32 bits ou 64 bits. processador de bits. Os blocos de construção básicos da ALU são somadores. Os circuitos somadores são construídos por portas lógicas e flip-flops. Os circuitos somadores semicondutores podem realizar adição em um tempo inferior a 1 microssegundo.
Vamos aprender sobre vários circuitos combinacionais – meio somador, somador completo, meio subtrator, subtrator completo, somador paralelo de N bits, subtrator paralelo de N bits, etc., que geralmente fazem parte de uma ALU.
Meio Somador –
O meio somador é um circuito combinacional simples que realiza a adição aritmética de dois dígitos binários ou a adição de dois bits. Possui duas entradas e duas saídas. As duas entradas são os dois números de 1 bit A e B, enquanto as duas saídas são a soma (S) de A e B e o transporte (C). A tabela verdade para um meio somador é a seguinte –
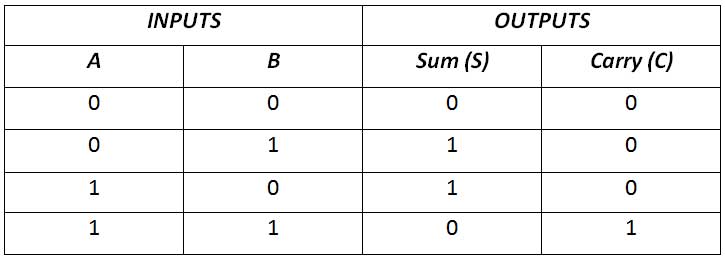
Figura 1: Tabela Verdade do Meio Somador
A partir da tabela verdade acima, deve ficar claro que a soma é 1 se qualquer uma das duas entradas for 1, caso contrário, se ambas as entradas forem 1 ou 0, a soma será 0. Isso pode ser implementado conectando as entradas a uma porta OR exclusiva. . O carry é 1 apenas se ambas as entradas forem 1, caso contrário, será 0. Isso pode ser implementado conectando as entradas à porta AND. Portanto, o meio somador tem o seguinte circuito –
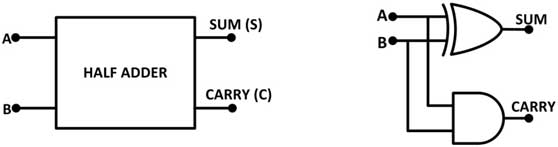
Fig. 2: Símbolo e Diagrama de Porta Lógica do Meio Somador
Somador completo –
Um meio somador tem apenas duas entradas e não há possibilidade de adicionar um transporte vindo dos bits de ordem inferior quando a adição de múltiplos bits é realizada. Para este propósito, o somador completo é projetado. Um somador completo é projetado para realizar a soma aritmética de três bits de entrada e produz uma saída de soma e um transporte. A tabela verdade para um somador completo é a seguinte –
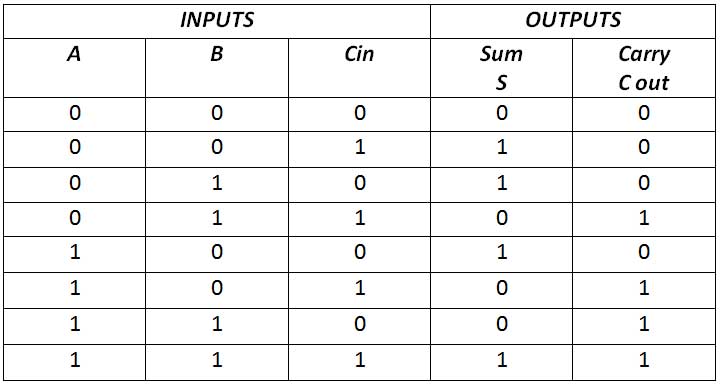
Fig. 3: Tabela Verdade do Somador Completo
A partir da tabela verdade, deve ficar claro que o somador completo tem três entradas e duas saídas. As duas variáveis de entrada são denotadas por A e B, que representam os dois bits significativos a serem adicionados. A terceira entrada Cin representa o carry da posição anterior de baixa significância. As saídas sãosoma (S) e transportar (C). A partir da tabela verdade, pode-se ver que a soma é 1 se uma das entradas for 1 ou todas as entradas forem 1. Isso pode ser implementado por OR exclusivo de todas as entradas. O carry é 1 quando duas entradas são 1 ou todas as entradas são 1. Isso pode ser implementado como soma da expressão do produto de todos os insumos. Portanto, o somador completo tem o seguinte circuito –
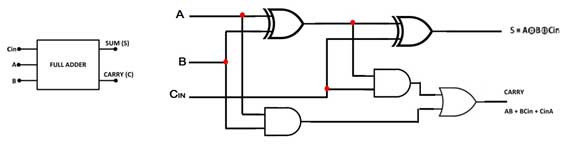
Fig. 4: Símbolo e Diagrama de Porta Lógica do Somador Completo
Pode-se notar que o somador completo é formado por dois circuitos meio somadores e uma porta OR.
Meio Subtrator –
O meio subtrator é um circuito combinacional simples projetado para realizar a subtração de dois bits. Possui duas entradas, X e Y e duas saídas Diferença (D) e Empréstimo (Bout). A tabela verdade para um meio subtrator é a seguinte –
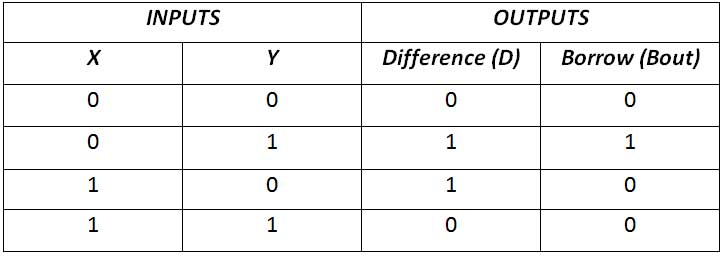
Fig. 5: Tabela Verdade do Meio Subtrator
A partir da tabela verdade, pode-se ver que a diferença D é 1 se uma das entradas for 1, caso contrário, se ambas as entradas forem 1 ou 0, o D é 0. Isso pode ser implementado conectando as entradas a uma porta OR exclusiva. O Borrow Out (Bout) é 1 apenas se Y for 1, mas não X. A saída de empréstimo Bout é 1 sempre que X for menor que Y, então a subtração é feita emprestando 1 do próximo bit de ordem superior. Isso pode ser implementado pela operação AND entre Y e NOT de X. Portanto, o meio subtrator tem o seguinte circuito –
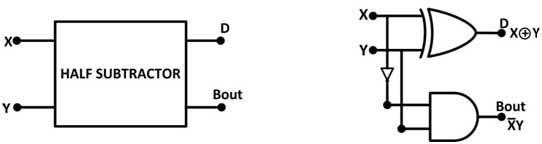
Fig. 6: Símbolo e Diagrama de Porta Lógica do Meio Subtrator
Subtrator Completo –
Um subtrator completo é projetado para realizar subtração envolvendo três bits, ou seja, bit minuendo, bit subtraendo e empréstimo do estágio anterior. No subtrator completo, possui três entradas X, Y e Bin, e duas saídas Diferença (D) e Empréstimo (Bout). Tem a seguinte tabela verdade –
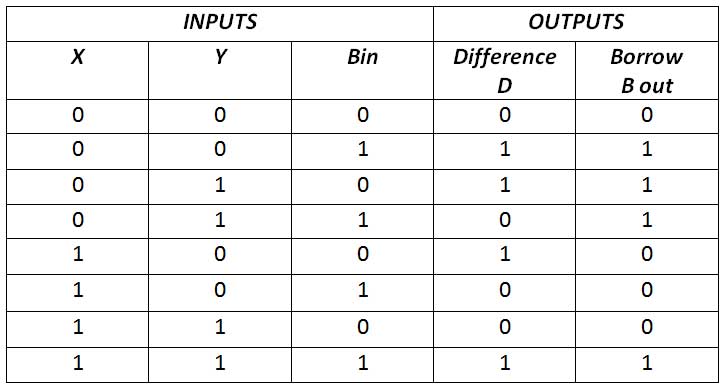
Fig. 7: Tabela Verdade do Subtrator Completo
A partir da tabela verdade, pode-se ver que a diferença é 1 se uma das entradas for 1 ou todas as entradas forem 1. Isso pode ser implementado por OR exclusivo de todas as entradas. O Borrow Out é 1 se duas entradasé 1 ou todas as entradas são 1. Isso pode ser implementado como operação OR entre dois meios subtratores. Portanto, o subtrator completo tem o seguinte diagrama de circuito –
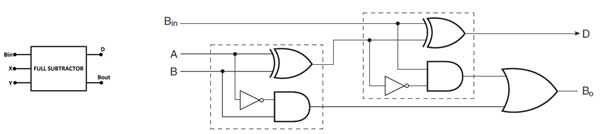
Fig. 8: Símbolo e Diagrama de Porta Lógica do Subtrator Completo
Somador paralelo de N bits –
O Full Adder é capaz de adicionar apenas dois números binários de um único dígito junto com uma entrada de transporte. Praticamente, é necessário adicionar números binários que são muito mais longos do que apenas um bit. Para adicionar dois números binários de n bits, é necessário usar o somador paralelo de n bits. Ele usa vários somadores completos em cascata. A saída de transporte do somador completo anterior é conectada à entrada de transporte do próximo somador completo.
Como um somador paralelo de 4 bits, pode ser construído conectando em cascata quatro circuitos somadores completos. No circuito A0 e B0 representam o LSB das palavras de quatro bits A e B onde Full Adder-0 é o estágio mais baixo. Conseqüentemente, seu Cin foi permanentemente tornado 0. O resto das conexões são exatamente as mesmas do somador paralelo de n bits. O somador paralelo de quatro bits é um circuito lógico muito comum. Um somador paralelo de 4 bits pode ser mostrado pelo seguinte diagrama de blocos –
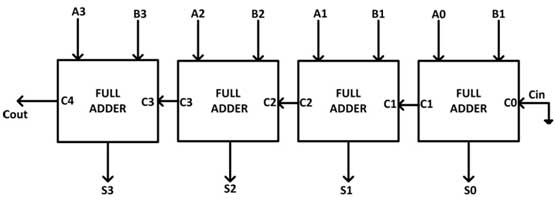
Fig. 9: Diagrama de porta lógica de somador paralelo de 4 bits
Subtrator paralelo de N bits –
A subtração pode ser realizada tomando o complemento de 1 ou 2 do número a ser subtraído. Por exemplo, a subtração (AB) pode ser realizada adicionando o complemento de 1 ou 2 de B a A. Portanto, um somador binário pode ser usado para realizar a subtração binária. Assim como um somador binário paralelo pode ser implementado conectando vários somadores completos em cascata, um subtrator binário paralelo também pode ser implementado conectando vários subtratores completos em cascata.
Como um subtrator paralelo binário de 4 bits que subtrai um número de 4 bits Y3 Y2 Y1 Y0 de outro número de 4 bits X3 X2 X1 X0 terá 4 saídas diferentes e saída emprestada (Bout). O Bin do subtrator completo LSB é conectado a 0 e o Bout do subtrator completo anterior é conectado ao Bin do próximo subtrator completo. Um subtrator paralelo de 4 bits pode ser mostrado pelo seguinte diagrama de blocos –
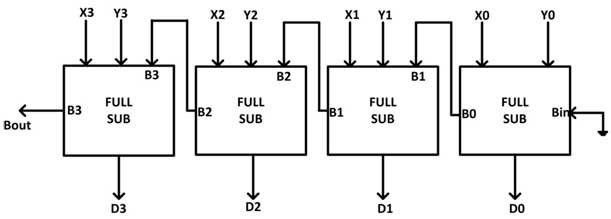
Fig. 10: Diagrama de porta lógica do subtrator paralelo de 4 bits
No próximo tutorial, aprenda sobre minimização de nível de porta e implementação de porta lógica dos circuitos aritméticos discutidos acima.

