1. Visão geral
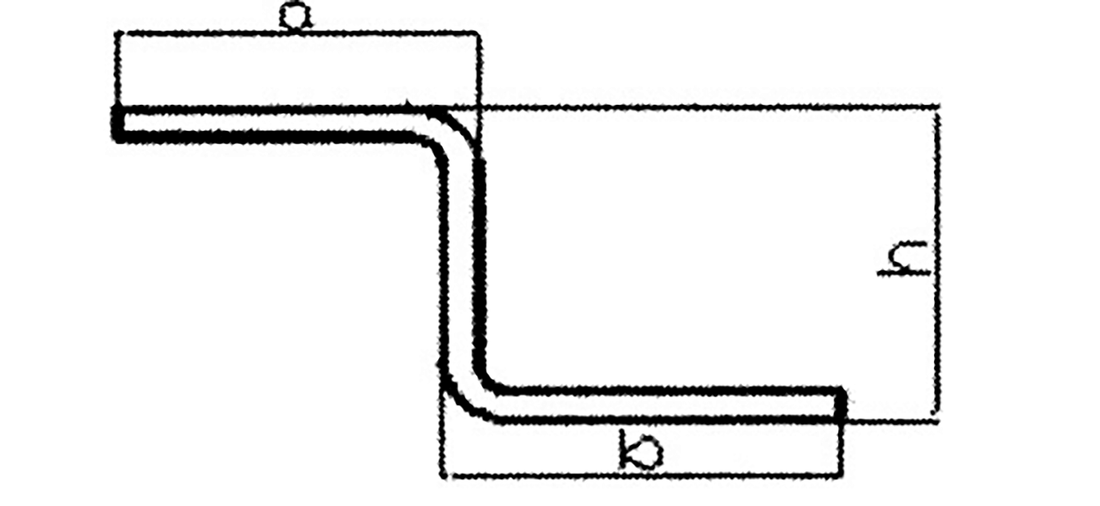
A peça dobrada em forma de Z mostrada na Figura 1 é uma peça comumente encontrada na produção. O tamanho de h é limitado pela matriz inferior, sendo o tamanho mínimo que pode ser dobrado pela matriz inferior existente mostrado na Tabela 1.
Tabela 1 Flexão de tamanho mínimo
| Espessura da placa | 1 | 1,5 | 2 | 2,5 | 3 |
| Tamanho mínimo | 7 | 9,5 | 14 | 16 | 18 |
Na produção prática, se houver numerosas matrizes de flexão em forma de Z menores que o tamanho mencionado, seria necessário o projeto de uma matriz de flexão composta para realizar a moldagem primária. Esta matriz composta pode ser usada para dobrar matrizes de dobra em forma de Z de vários tamanhos em diferentes materiais de folha.
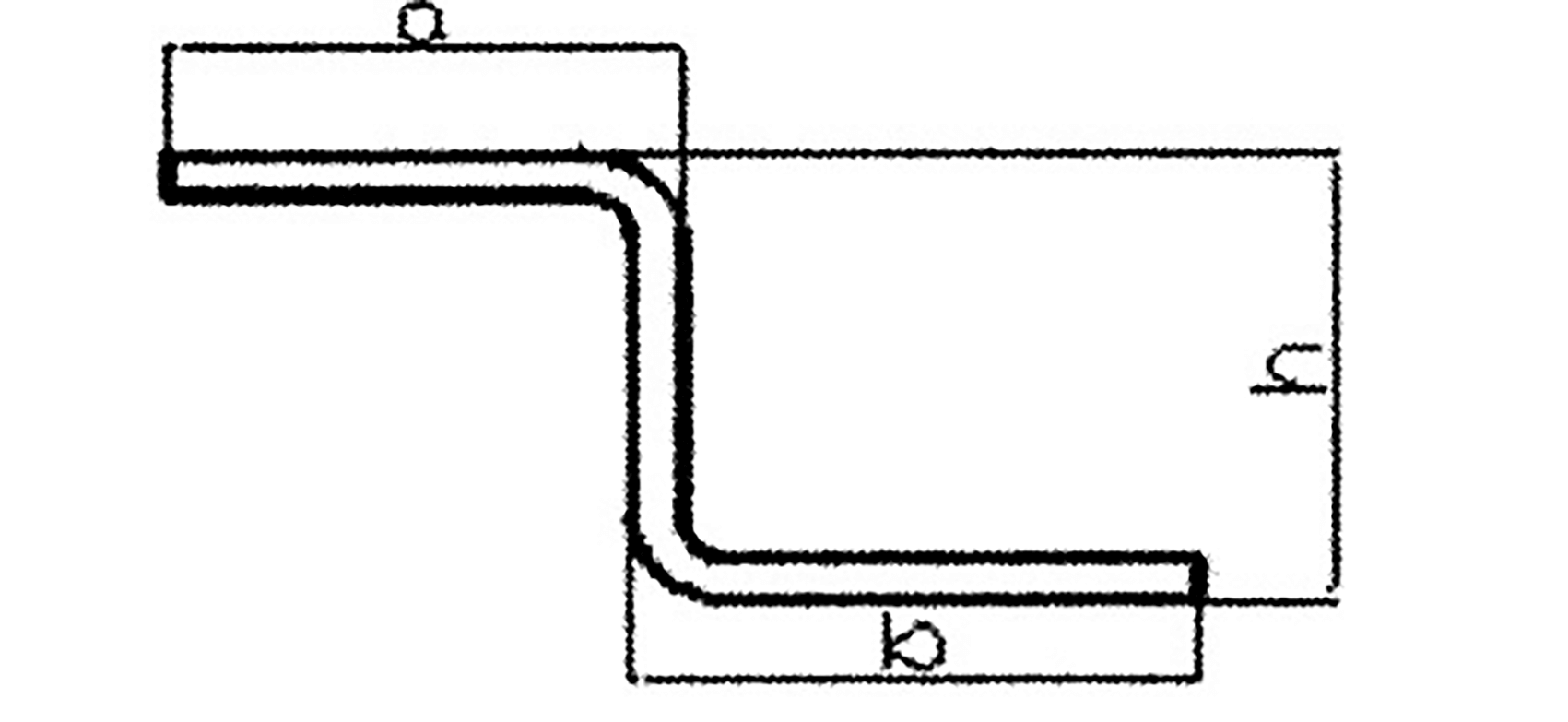
Fig. 1 Matriz de flexão em forma de Z
2. O processo de deformação por flexão
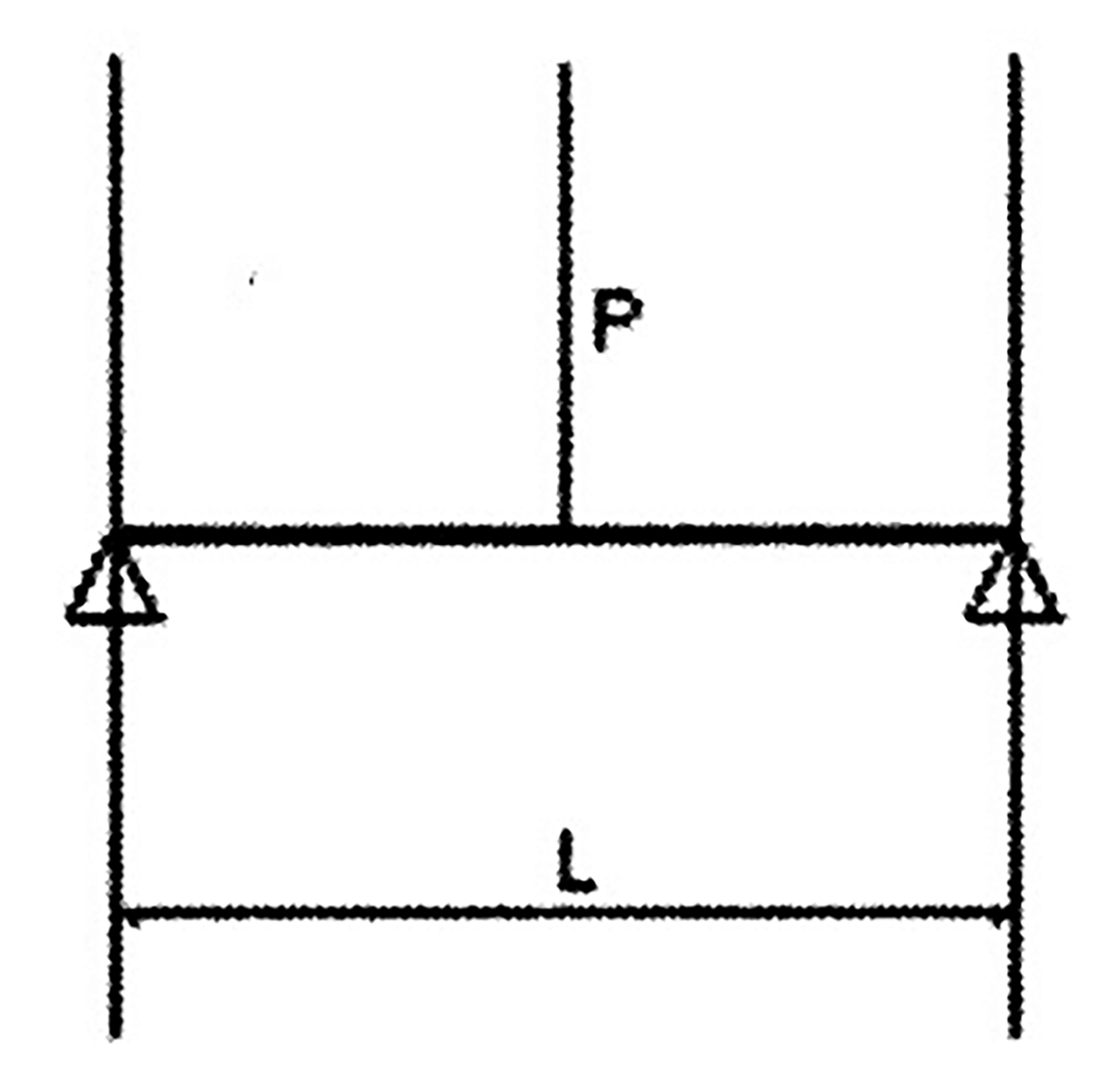
Fig. 2 Diagrama de força de ação
Conforme representado na Figura 2, quando uma chapa metálica é submetida à flexão, ela sofre momento fletor, força de cisalhamento e pressão local. No entanto, o principal efeito da deformação por flexão é o momento fletor.
A aplicação de força externa leva à correspondente deformação da chapa metálica, o que também desencadeia o aparecimento de força interna que resiste à deformação. A força interna se equilibra com a força externa e é medida como tensão, que é a força interna por unidade de área do objeto. Quanto maior a força externa, maior a tensão e a deformação.
Quando a tensão externa do material está abaixo do seu limite elástico, a chapa metálica está em um estado de deformação elástica. De acordo com a lei de Hooke, a relação linear entre tensão e deformação na seção se deve à mudança linear na distância entre a deformação e a camada central (alongamento da camada externa e encurtamento da camada interna).
Se a força externa for removida, a chapa metálica retorna à sua forma original. No entanto, se a força externa continuar a aumentar, o grau de deformação da peça dobrada continuará a aumentar até que a tensão causada pela força externa seja igual ao limite de escoamento do material, levando à deformação plástica do material externo.
À medida que a força externa aumenta, a deformação plástica progride da superfície para o centro. Uma vez removida a força externa, a deformação elástica desaparece imediatamente, mas a deformação plástica permanece e resulta em deformação por flexão permanente.
Se a tensão causada pela força externa exceder o limite de resistência do material, a chapa metálica sofre uma fratura por deformação plástica. A compressão interna durante a flexão de chapas metálicas também produz deformação plástica, mas esse tipo de deformação plástica aumenta a tensão na superfície sem causar danos e, portanto, é frequentemente ignorada.
3. Cmétodo de cálculo de flexão
Agora observamos cuidadosamente a deformação plástica por flexão.
Sob a ação do momento fletor, existem três linhas iguais na seção da placa: ab= a1b1 = um2b2.
Após a flexão, a camada interna encurta e a camada externa se alonga, ou seja, ab < a1b1
Portanto, durante a flexão, o material interno é submetido à compressão e fica mais curto, enquanto o material externo é esticado e alongado.
Entre a tensão e a compressão, existe uma camada de material que não sofre nem alongamento nem compressão e é chamada de camada neutra. Esta camada permanece inalterada em comprimento e não alonga nem encurta.
O processo de cálculo da peça dobrada envolve dividi-la em vários elementos geométricos básicos, incluindo segmentos de linha reta e segmentos de arco. O comprimento de cada elemento é calculado individualmente e o comprimento total de todos os elementos é o comprimento desdobrado da peça dobrada.
A parte dobrada em forma de Z na Figura 1 pode ser dividida em cinco unidades, conforme mostrado na Figura 2. As unidades 1, 3 e 5 são segmentos de linha reta, enquanto as unidades 2 e 4 são segmentos de arco.
Conforme discutido anteriormente, a camada de fibra com comprimento constante no meio antes e depois da flexão é chamada de camada neutra. Ao calcular o comprimento de expansão do segmento de arco, na verdade está calculando o comprimento da camada neutra do segmento de arco.
A posição, x, da camada neutra do lado interno do arco (como mostrado na Figura 3) é geralmente determinada pela razão r/t.
x =kt
Onde:
- t — Espessura do material
- k — Coeficiente de posição da camada neutra (ou coeficiente da camada neutra)
- k = R – r/t
- R = r +kt
Onde:
- R — A distância do centro do raio r até a linha neutra de flexão
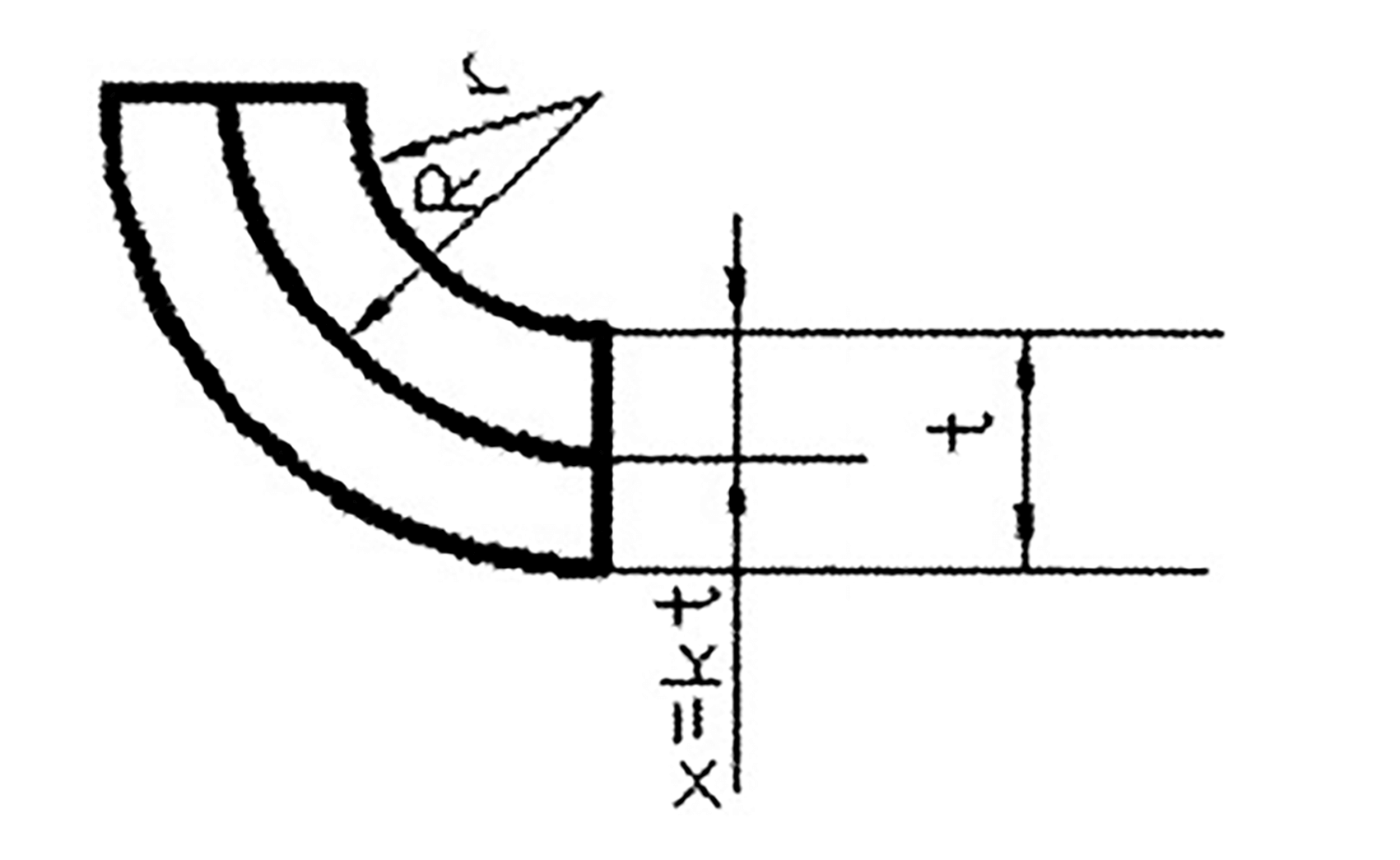
Figura 3
O valor de k varia com a relação entre o raio interno e a espessura da chapa, mostrada na Tabela 2:
mesa 2
| r/t | 0,25 | 0,5 | 1 | 2 | 3 | 4 |
| k | 0,26 | 0,33 | 0,35 | 0,375 | 0,4 | 0,415 |
Na produção prática, é mais comum dobrar placas de aço em um formato de 90 graus.
O cálculo do comprimento do arco para flexão de 90 graus com diferentes valores de r e t pode ser obtido através de tabelas de referência em aplicações práticas.
Este artigo se concentra na dobra em ângulo reto de 90 graus, mas não é eficiente calcular a linha reta e os segmentos de arco separadamente para peças com dobra de chapa metálica em 90 graus. Em vez disso, eles são marcados conforme mostrado na Figura 1.
Ao calcular o material desdobrado, podemos usar diretamente as dimensões marcadas para simplificar o processo de cálculo.
Conforme a figura 1, calcula-se o comprimento do material desenvolvido:
L = a+b+h – 2x
Onde:
- x — Coeficiente de flexão comum
4. Estrutura e processo de trabalho da matriz composta de dobra em forma de Z
Tabela 3 Coeficiente de flexão comum x
| Espessura da placa t | Raio de curvatura interno r | |||
|---|---|---|---|---|
| 1,0 | 1,5 | 2,0 | 2,5 | |
| 0,5 | 1,0 | 1.2 | 1.4 | 1.6 |
| 1 | 1,9 | 2.1 | 2.3 | 2,5 |
| 1,5 | 2,5 | 2.7 | 2.9 | 3.1 |
| 2,0 | 3.4 | 3.6 | 3.8 | 4,0 |
| 2,5 | 4,0 | 4.2 | 4.4 | 4.6 |
| 3 | 4.9 | 5.1 | 5.3 | 5.4 |
Esta matriz de conjunto simples é diferente da matriz convencional.
Ele foi projetado para ser simples, rápido, fácil de processar e direto de formar. Embora possa não ser tão preciso quanto a matriz convencional, ainda é usado para processar produtos com rapidez e precisão.
O diagrama de formação da matriz composta é mostrado na Tabela 3.
Princípio de processamento: A espessura da junta é ajustada para atingir a largura desejada da ranhura em V na matriz superior e inferior e para realizar um processamento único de dobra em Z sob pressão.
Estrutura da matriz: A matriz de flexão em forma de Z consiste em uma matriz superior, uma matriz inferior, uma gaxeta e um aço prismático angular.
Espessura da junta: O espaçador é feito de aço com 0,5 mm de espessura e é empilhado para atingir a espessura necessária.
Aço Prisma: Uma peça de aço retangular dentro da matriz, seus quatro ângulos são chanfrados em lados de 0,5 mm, 1,0 mm, 2,0 mm e 4,0 mm, conforme mostrado na Tabela 3.
A matriz simples especial é usada para atingir a largura desejada da ranhura em V da matriz superior e inferior, ajustando o tamanho do aço do prisma angular e a espessura da gaxeta e, em seguida, realizando o processamento de dobra em Z em uma prensa.
Este método é escolhido devido ao potencial de aumentar a ranhura em V e reduzir vincos, de modo que diferentes espessuras de placa requerem dentes diferentes, conforme mostrado na Tabela 4.
Tabela 4
| Espessura da placa | t<0,8 | 0,8 |
1,0 |
1,2 |
t>1,5 |
| Ponta | 0,5 | 1,0 | 1,0 ou 2,0 | 2,0 | 4,0 |
Método de depuração da matriz de dobra em forma de Z:
1) Ambas as dobras da dobra Z de borda reta são 90°. A distância entre as duas pontas da ferramenta é: 1,414/2×h;
2) Se o vinco da peça for muito profundo, será necessário escolher um ângulo grande.
b: ferro de passar; c: aumenta o ângulo R;
3) Se a altura for atingida, mas o ângulo for maior que 90°, então a: excentricidade da matriz.
b: Aumentar a espessura do calço;
4) Se os dois lados da dobra Z não forem paralelos, isso pode ser conseguido aumentando ou diminuindo a espessura do calço.
Se a dobra superior for maior que 90°, a espessura do calço inferior da matriz precisa ser aumentada; e se a dobra inferior for maior que 90°, a espessura do calço superior da matriz precisa ser aumentada.
Método de cálculo de expansão de curvatura Z:
Quando h > tamanho normal de dobra, deve desdobrar-se em duas dobras.
eu = uma + b + h – 2x
Onde:
- l – Comprimento do material desdobrado
Quando h < o tamanho normal de flexão, ele é expandido pela conformação em uma etapa.
L = a + B + h – 1,5x
Onde:
- x — Coeficiente de flexão comum
Uma das fórmulas empíricas na prática é subtrair 1,5x da dimensão total de uma moldura.