No campo do projeto de chapas metálicas, termos como tolerância de dobra, dedução de dobra e fator K são frequentemente ouvidos. Mas o que exatamente esses termos significam? E como podemos calculá-los?
Nesta postagem, forneceremos respostas detalhadas a essas perguntas.
1. Introdução ao método de cálculo de chapa metálica
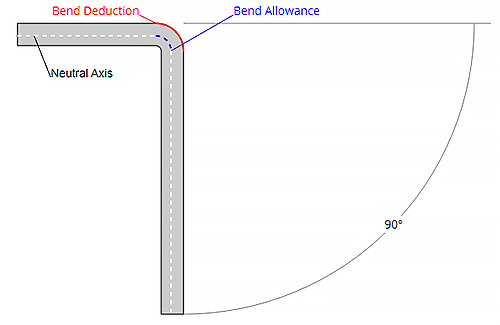
Engenheiros e vendedores envolvidos no projeto e produção de peças de chapa metálica usam vários algoritmos para calcular o comprimento real do material em seu estado desdobrado para garantir as dimensões desejadas da peça após a dobra e conformação final.
O método mais comumente utilizado é a simples “regra de pinçamento do dedo”, um algoritmo baseado na experiência pessoal, que leva em consideração fatores como o tipo e espessura do material, o raio e ângulo de dobra, o tipo de máquina e o velocidade de flexão.
Com o surgimento da tecnologia computacional, o design auxiliado por computador (CAD) é cada vez mais usado para aproveitar as vantagens das capacidades analíticas e computacionais superiores do computador.
No entanto, mesmo quando um programa de computador simula o dobramento ou desdobramento de chapas metálicas, ele ainda precisa de um método para cálculo preciso.
A maioria dos sistemas comerciais de modelagem de sólidos CAD e 3D fornecem uma solução geral e poderosa para isso e geralmente são compatíveis com o método original de regra de pinçamento e oferecem opções de personalização para inserir conteúdo específico em seu processo de cálculo.
O SolidWorks é líder no fornecimento desse recurso para projetos de chapas metálicas.
Concluindo, dois algoritmos populares de dobra de chapa metálica são amplamente adotados hoje: um baseado na tolerância de dobra e outro baseado na dedução de dobra.
Para melhorar a compreensão dos leitores sobre os conceitos básicos no cálculo de projetos de chapas metálicas, os seguintes pontos serão resumidos e explicados:
- As definições dos dois algoritmos de dobra: tolerância de dobra e dedução de dobra, e sua conexão com a geometria real da chapa metálica.
- A relação entre a dedução de dobra e a margem de dobra e como os usuários que usam o algoritmo de dedução de dobra podem converter facilmente seus dados para o algoritmo de margem de dobra.
- A definição do fator K, seu uso prático e a faixa de valores do fator K aplicáveis para diferentes tipos de materiais.
2. Método de tolerância à flexão
Para uma compreensão mais clara da tolerância de dobra, consulte a Figura 1, que ilustra uma única dobra em um componente de chapa metálica. A Figura 2 exibe a peça em seu estado desdobrado.
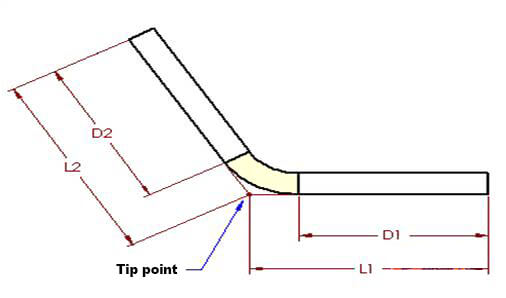
figura 1
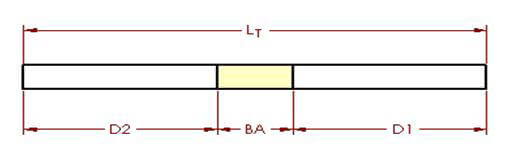
Figura 2
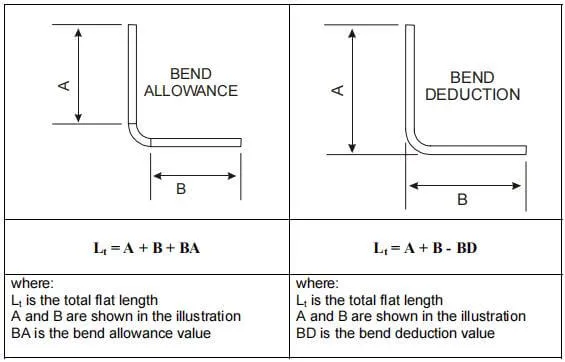
O algoritmo de margem de flexão descreve o comprimento desdobrado (LT) de uma peça de chapa metálica como a soma dos comprimentos de cada segmento após a peça ser planificada, mais o comprimento da área de dobra planificada.
A tolerância de dobra (BA) representa o comprimento da área de dobra achatada. Assim, o comprimento total da peça pode ser expresso como equação (1):
LT = D1 + D2 + BA (1)
A área de dobra (ilustrada em amarelo claro na ilustração) é a área que teoricamente sofre deformação durante o processo de dobra.
Para determinar a geometria da peça desdobrada, siga estes passos:
- Corte a área dobrada da parte dobrada.
- Coloque as duas seções planas restantes em uma superfície plana.
- Calcule o comprimento da área de dobra achatada.
- Junte a área de dobra achatada entre as duas seções planas e o resultado será a peça desdobrada desejada.
A tarefa de determinar o comprimento da área de flexão achatada, representada por BA na figura, é um pouco mais desafiadora.
O valor de BA varia com base em fatores como tipo de material, espessura do material, raio e ângulo de curvatura, bem como processo de dobra, tipo de máquina e velocidade da máquina.
O valor do BA pode ser obtido de várias fontes, incluindo fornecedores de materiais de chapa metálica, dados experimentais, experiência e manuais de engenharia.
No SolidWorks, pode-se inserir valores BA diretamente ou usar o fator K (que será discutido mais tarde) para calcular os valores.
O método da mesa de dobra é a maneira mais precisa de especificar diferentes tolerâncias de dobra para diferentes situações com diferentes espessuras, raios e ângulos.
A criação da mesa de dobra inicial pode levar algum tempo, mas uma vez formada, partes dela podem ser reutilizadas no futuro.
Informações iguais ou diferentes podem ser inseridas para cada dobra da peça.
1) Padrões para flexão comum
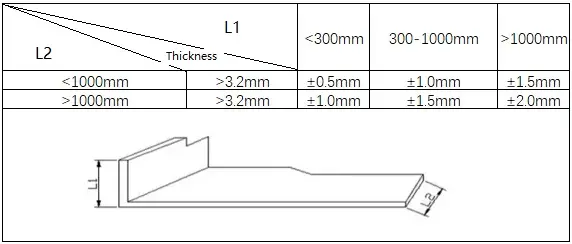
2) Padrões para flexão Z
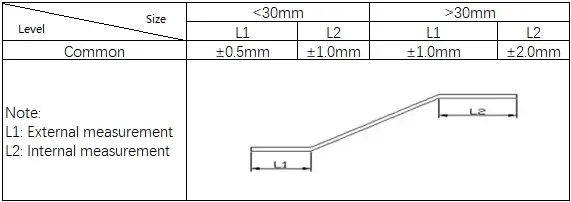
3) Padrões para flexão em V
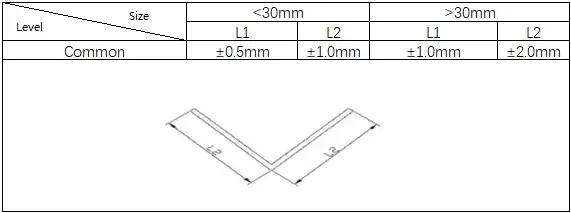
4) Padrões para flexão em U
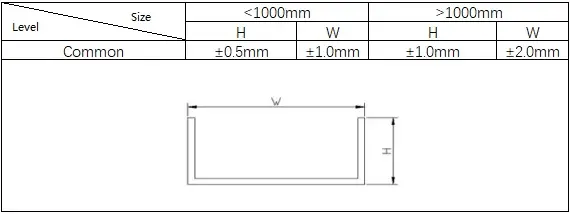
Leitura relacionada: Calculadora de força de flexão em forma de V e U
3. Método de dedução de flexão
Dedução de dobra é um termo usado para descrever a quantidade de recuo no processo de dobra de chapa metálica. Este é outro algoritmo simples para descrever o processo.
As Figuras 1 e 2 também se aplicam a este conceito. De acordo com o método de dedução de flexão, o comprimento achatado (LT) da peça é igual à soma dos comprimentos das duas seções planas que se estendem até o “ponto de ponta” (a intersecção hipotética das duas seções planas), menos a flexão dedução (BD).
Assim, o comprimento total da peça pode ser expresso conforme mostrado na equação (2):
LT = L1 + L2 – BD (2)
O valor de BD pode ser determinado ou obtido de diversas fontes, como fornecedores de materiais de chapa metálica, dados experimentais, experiência, manuais de engenharia com equações ou tabelas, etc.
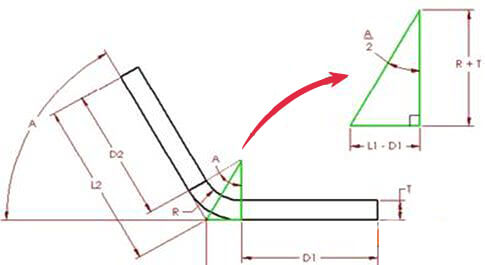
Figura 3
4. Relação entre flexão mesada e dedução de flexão
É importante que os usuários familiarizados com o método Dedução de dobra compreendam a relação com o método Tolerância de dobra, que é comumente adotado no SolidWorks.
A relação entre os dois valores pode ser facilmente deduzida usando as duas geometrias de flexão e desdobramento das peças.
Comparando as equações (1) e (2), temos:
LT = D1 + D2 + BA (1) LT = L1 + L2 – BD (2)
E portanto,
D1 + D2 + BA = L1 + L2 – BD (3)
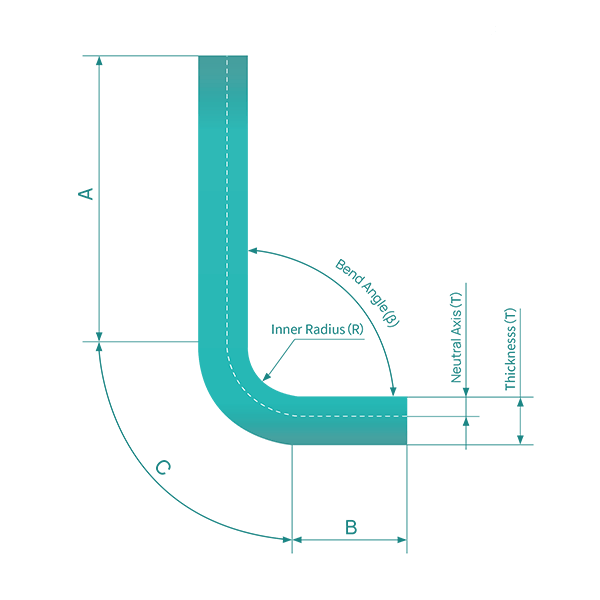
Na Figura 3, o ângulo A representa o ângulo de flexão, que descreve o ângulo varrido pela peça durante a flexão, e também o ângulo do arco formado pela área de flexão, que é mostrado em duas metades.
Usando as dimensões e princípios dos triângulos retângulos, podemos derivar as seguintes equações:
D1 = L1 – (R + T)TAN(A/2) (4) D2 = L2 – (R + T)TAN(A/2) (5)
Substituindo as equações (4) e (5) na equação (3), podemos obter a relação entre BA e BD:
BA = 2(R + T)TAN(A/2) – BD (6)
E quando o ângulo de curvatura é de 90 graus, esta equação é simplificada para:
BA = 2(R + T) –BD (7)
Estas equações (6) e (7) fornecem um método conveniente para conversão de um algoritmo para outro, usando apenas a espessura do material, ângulo/raio de curvatura, etc.
Para usuários do SolidWorks, essas equações fornecem um método direto para converter a dedução de dobra em tolerância de dobra.
O valor da tolerância de dobra pode ser usado para toda a peça ou para cada dobra individual, ou pode ser incluído em uma tabela de dados de dobra.
5. Método do fator K
O fator K é um valor independente que explica a flexão e o desdobramento de chapas metálicas em vários cenários geométricos.
É também um valor autônomo usado para calcular a tolerância de flexão (BA) sob diversas condições, como diferentes espessuras de material, ângulos de flexão e raios.
As Figuras 4 e 5 são fornecidas para ajudar a esclarecer a definição aprofundada do fator K.
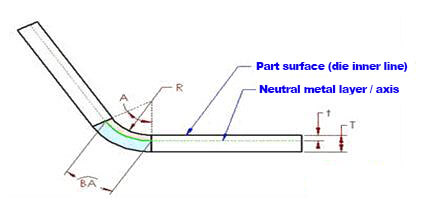
Figura 4
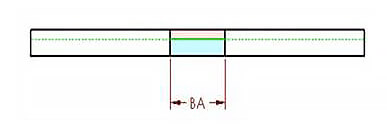
Figura 5
Podemos confirmar que existe um eixo neutro na espessura da peça em chapa. O material da chapa metálica neste eixo neutro na região de flexão não é esticado nem comprimido, o que significa que é a única área que não se deforma durante a flexão.
As Figuras 4 e 5 mostram o limite entre as regiões rosa e azul.
Durante a flexão, a região rosa se comprime e a região azul se estende. Se a camada neutra da chapa metálica permanecer indeformada, o comprimento do seu arco na região de dobra permanece o mesmo, quer a peça seja dobrada ou achatada.
Como resultado, a tolerância de flexão (BA) deve ser igual ao comprimento do arco da camada neutra na região de flexão da peça de chapa metálica, que é mostrada em verde na Figura 4.
A posição da camada neutra da chapa metálica depende das propriedades de um material específico, como a ductilidade.
Supõe-se que a distância entre a camada neutra da chapa metálica e a superfície é “t”, ou a profundidade da superfície da peça da chapa metálica até o material na direção da espessura.
Como resultado, o raio do arco da camada neutra pode ser expresso como (R + t). Usando esta expressão e o ângulo de flexão, o comprimento do arco da camada neutra (BA) pode ser calculado.
BA = Pi(R+T)A/180
Para simplificar a definição da camada neutra da chapa metálica e torná-la aplicável a todos os materiais, foi introduzido o conceito do fator K.
A definição do fator K é: é a relação entre a espessura da camada neutra da chapa metálica e a espessura total do material da peça da chapa metálica. Em outras palavras, o fator K é definido como:
K = t/T
Portanto, o valor de K estará sempre dentro da faixa de 0 a 1. Se um fator K for 0,25, indica que a camada neutra está situada em 25% da espessura total do material da chapa metálica.
Da mesma forma, se for 0,5 significa que a camada neutra está localizada em 50% de toda a espessura e assim por diante.
Combinando as equações mencionadas acima, a seguinte equação (8) pode ser obtida:
BA = Pi(R+K*T)A/180 (8)
Portanto, o valor de K estará sempre entre 0 e 1.
Se o fator K for 0,25, significa que a camada neutra está localizada em 25% da espessura do material da chapa metálica da peça.
Da mesma forma, se for 0,5 significa que a camada neutra está localizada em 50% de toda a espessura e assim por diante.
A origem do fator K pode ser rastreada até fontes tradicionais, como fornecedores de materiais de chapa metálica, dados de testes, experiência, manuais, etc.
No entanto, em alguns casos, o valor fornecido pode não ser expresso como um fator K claro, mas ainda é possível encontrar a relação entre eles.
Por exemplo, se um manual ou literatura descreve o eixo neutro como “posicionado a 0,445x a espessura do material da superfície da chapa metálica”, isso pode ser interpretado como um fator K de 0,445, significando k = 0,445.
Quando este valor de K é substituído na equação (8), a seguinte fórmula pode ser obtida.
BA = A (0,01745R + 0,00778T)
Se a equação (8) for modificada por outro método, a constante na equação (8) for calculada e todas as variáveis forem retidas, pode-se obter o seguinte:
BA = A (0,01745 R + 0,01745 K*T)
Ao comparar as duas equações, é fácil determinar que 0,01745 * k = 0,00778 e, portanto, k pode ser calculado como 0,445.
Foi descoberto que o sistema SolidWorks também fornece um algoritmo de tolerância de dobra para materiais específicos quando o ângulo de dobra é de 90 graus. A fórmula de cálculo para cada material é a seguinte:
- Latão macio ou cobre macio: BA = (0,55 * T) + (1,57 * R)
- Cobre semiduro ou materiais como latão, aço-carbono e alumínio: BA = (0,64 * T) + (1,57 * R)
- Bronze, cobre duro, aço laminado a frio e aço para molas: BA = (0,71 * T) + (1,57 * R)
Na verdade, simplificando a equação (7) e definindo o ângulo de flexão para 90 graus, a constante pode ser calculada e a equação pode ser transformada da seguinte forma:
BA = (1,57 * K * T) + (1,57 *R)
Portanto, comparando a fórmula de cálculo acima, o valor de K para materiais de latão macio ou cobre macio pode ser obtido como 1,57xk = 0,55 ou K = 0,35.
Usando o mesmo método, é fácil calcular os valores do fator K para os diversos tipos de materiais listados acima.
- Latão macio ou material de cobre macio: K = 0,35
- Cobre semi-duro ou materiais como latão, aço macio e alumínio: K = 0,41
- Bronze, cobre duro, aço laminado a frio e aço para molas: K = 0,45
Conforme discutido anteriormente, existem diversas fontes das quais o valor do fator K pode ser obtido, como fornecedores de materiais, dados de testes, experiência e manuais.
Para estabelecer um modelo preciso de chapa metálica usando o método do fator K, é crucial encontrar a fonte apropriada do fator K que atenda aos seus requisitos de engenharia. Isso garantirá que os resultados da parte física sejam tão precisos quanto desejado.
Em algumas situações, pode não ser possível obter resultados precisos utilizando apenas um único valor do fator K, especialmente quando é necessário acomodar uma ampla gama de cenários de flexão.
Nesses casos, é aconselhável usar o valor da tolerância de dobra (BA) diretamente para uma única dobra de toda a peça, ou usar uma tabela de dobra para descrever os diferentes valores de BA, dedução de dobra (BD) ou fator K correspondentes a valores diferentes de A, R e T em todo o intervalo.
Além disso, as equações podem ser usadas para gerar dados como o exemplo da tabela de dobras fornecida pelo SolidWorks. Se necessário, as células da tabela de dobras também podem ser modificadas com base em dados experimentais ou empíricos.
O diretório de instalação do SolidWorks inclui tabelas de tolerâncias de dobra, tabelas de dedução de dobra e tabelas de fator K, que podem ser editadas e personalizadas conforme necessário.
- Calculadora de dobra de chapa metálica
6. Resumo
Esta postagem fornece uma visão geral abrangente dos métodos de cálculo comuns e seus princípios subjacentes usados no projeto e fabricação de peças de chapa metálica.
Abrange o cálculo de subsídios de flexão, deduções de flexão e fatores K, e explica as diferenças entre esses métodos e suas inter-relações.
Ele serve como uma referência útil para engenheiros e profissionais técnicos do setor.
Observação:
- Tan refere-se à representação simplificada da função trigonométrica tangente.
- PI representa a constante pi (3,14159265…).

























































