A avaliação precisa da qualidade das estruturas de aço em serviço requer a determinação do grau e da resistência do aço. Esta é a base para testes e avaliações confiáveis.
O método convencional para determinar a resistência do aço é extrair amostras da estrutura para testes de tração, mas esta abordagem pode causar danos à estrutura original e pode não ser viável para certas estruturas.
Assim, é crucial utilizar métodos de ensaios não destrutivos para calcular o grau e a resistência do aço.
Pesquisadores nacionais e internacionais investigaram métodos de testes não destrutivos para determinar a resistência do aço em locais de engenharia. Eles se concentraram principalmente na composição química e na dureza e desenvolveram algumas fórmulas empíricas.
Leitura relacionada: Dureza do metal: o guia definitivo (com gráfico de dureza)
Essas fórmulas empíricas podem ser categorizadas em dois tipos:
O primeiro tipo envolve o cálculo da resistência à tração com base na composição química, conforme especificado na fórmula da Norma Técnica GB/T 50621-2010 para Ensaios no Local de Estruturas de Aço. No entanto, a resistência dos materiais de aço é afetada pela composição química e pelo processo de fabricação (como fundição, forjamento, laminação e tratamento térmico), portanto, confiar apenas na composição química para calcular a resistência do aço pode resultar em um desvio significativo.
O segundo tipo envolve o cálculo da resistência à tração com base na dureza. A pesquisa mostrou que existe uma correlação positiva entre a dureza e a resistência à tração do aço. A resistência à tração dos materiais pode ser estimada a partir dos resultados dos testes de dureza, que é um método amplamente utilizado na prática de engenharia.
Atualmente, os principais padrões nacionais que podem ser utilizados para esse fim são GB/T 33362-2016 Conversão de Valores de Dureza de Materiais Metálicos e GB/T 1172-1999 Conversão de Dureza e Resistência de Metais Ferrosos. GB/T 33362-2016 é equivalente à conversão ISO 18265:2013 de valores de dureza de materiais metálicos. A tabela de conversão de dureza para aço não ligado, aço de baixa liga e aço fundido na Tabela A.1 desta norma foi obtida através de testes de comparação com medidores de dureza verificados e calibrados em diferentes laboratórios pela Associação Alemã de Engenheiros Metalúrgicos. GB/T 1172-1999 foi obtido através de extensos testes e pesquisas por instituições como a Academia Chinesa de Metrologia. A Tabela 2 da norma fornece principalmente a relação de conversão aplicável ao aço de baixo carbono.
No entanto, nenhum destes padrões fornece dados confiáveis com significância estatística para a incerteza dos valores de conversão, e a faixa de desvio dos resultados de conversão é desconhecida. Os pesquisadores estudaram a correlação entre dureza e resistência do aço utilizado na construção de estruturas de aço por meio de análise de regressão e compararam-na com os padrões nacionais, que servem como verificação e complemento aos padrões GB/T 33362-2016 e GB/T 1172-1999. Eles também discutiram o método de detecção adequado para locais de projetos de estruturas metálicas, incorporando os instrumentos de detecção portáteis existentes.
1. Amostra de teste
Os objetos de pesquisa deste estudo são as placas de aço Q235 e Q345 comumente utilizadas na engenharia de estruturas metálicas.
Leitura relacionada: Aço Q235 vs Q345
A fim de garantir amostras representativas, 162 placas de aço foram coletadas de 86 fabricantes de estruturas de aço na província de Jiangsu, compreendendo 82 peças de placas de aço Q235 e 80 peças de placas de aço Q345. As especificações de espessura das placas de aço foram 6, 8, 10, 12, 14, 18, 20 e 30 mm.
As placas de aço foram processadas em amostras de tiras de 20 mm x 400 mm e os testes de tração foram realizados usando uma máquina de teste de tração servo eletro-hidráulica controlada por microcomputador, de acordo com os requisitos da GB/T 228.1-2010.
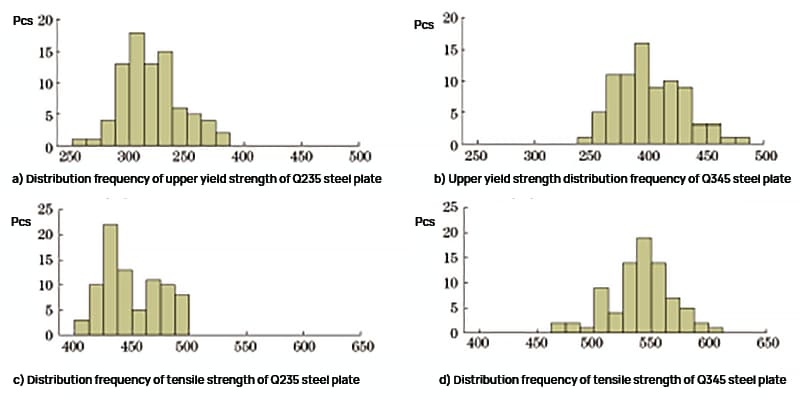
Os resultados dos testes de resistência ao escoamento superior e resistência à tração das placas de aço Q235 e Q345 foram analisados estatisticamente, e a frequência de distribuição é mostrada na Figura 1.
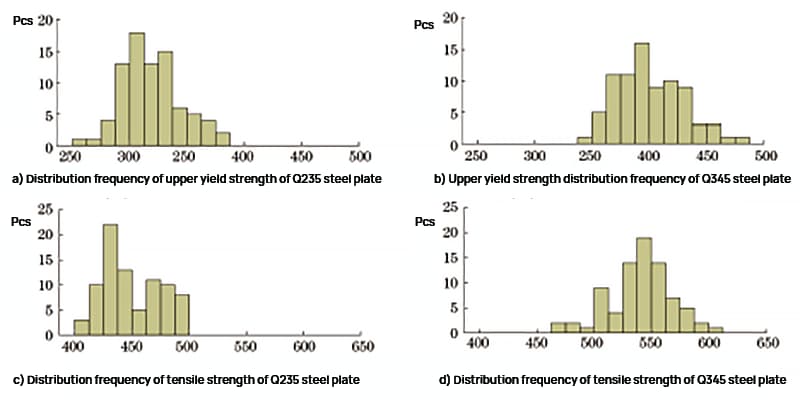
Fig. 1 Frequência de distribuição de resistência da placa de aço Q235 e da placa de aço Q345
Conforme mostrado na Figura 1, a faixa superior de resistência ao escoamento da placa de aço Q235 é de 261 a 382 MPa, e a faixa de resistência à tração é de 404 a 497 MPa. A faixa superior de resistência ao escoamento da placa de aço Q345 é de 345 a 477 MPa, e a faixa de resistência à tração é de 473 a 607 MPa.
A distribuição de frequência de intensidade é aproximadamente normal e os resultados dos testes estão alinhados com os dados de inspeção diária, indicando que as amostras são altamente representativas.
2. Resultados e análises de testes
As amostras de teste foram coletadas e processadas de acordo com os requisitos da norma e submetidas a testes de dureza Rockwell, dureza Vickers, dureza Brinell e tração.
Para realizar a análise de regressão dos resultados dos ensaios de dureza e resistência, foi utilizado o método dos mínimos quadrados e empregou-se o software SPSS.
2.1 Correlação entre dureza e resistência Rockwell
2.1.1 Resultados e análises do teste de dureza Rockwell
A superfície da amostra foi lixada com um moedor para garantir que ficasse plana e lisa. A escala B foi selecionada e o instrumento foi calibrado utilizando um bloco de dureza padrão. O teste de dureza Rockwell foi realizado de acordo com os requisitos do teste de dureza Rockwell de materiais metálicos GB/T 230.1-2018, parte 1: método de teste. Foram medidos três pontos para cada amostra e obtido o valor médio.
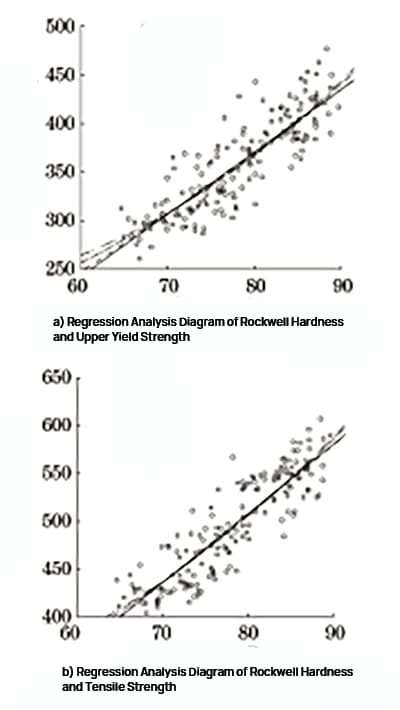
Fig. 2 Análise de regressão da dureza e resistência Rockwell
O software SPSS foi utilizado para realizar regressão linear, regressão quadrática, regressão de potência e análise de regressão exponencial na dureza Rockwell, limite de escoamento superior e resistência à tração. O diagrama da análise de regressão está representado na Figura 2, e os resultados da análise de regressão são apresentados na Tabela 1 e na Tabela 2.
Tabela 1 Dados do modelo de regressão de dureza Rockwell e limite de escoamento superior
| Equação | Resumo do modelo | Parâmetro do modelo | ||||
| R2 | F | Significância P | constante | b1 | b2 | |
| Expoente quadrático linear | 0,736 | 446.897 | 0,000 | -143.077 | 6.426 | 0,081 |
| 0,741 | 227.290 | 0,000 | 341.852 | -6.141 | ||
| 0,740 | 456.461 | 0,000 | 0,828 | 1.392 | ||
| 0,744 | 464.965 | 0,000 | 86.806 | 0,018 | ||
Tabela 2 Dados do modelo de regressão de dureza Rockwell e resistência à tração
| Equação | Resumo do modelo | Parâmetro do modelo | ||||
| R2 | F | Significância P | constante | b1 | b2 | |
| Expoente quadrático linear | 0,780 | 565.900 | 0,000 | -71.394 | 7.241 | 0,074 |
| 0,783 | 286.412 | 0,000 | 372.980 | -4,274 | ||
| 0,778 | 560.887 | 0,000 | 3.477 | 1.137 | ||
| 0,782 | 574.207 | 0,000 | 155.315 | 0,015 | ||
Conforme indicado pela Tabela 1 e Tabela 2, a dureza Rockwell tem uma forte correlação com a resistência, e a correlação com a resistência à tração é mais forte em comparação com a resistência ao escoamento superior.
Dos quatro modelos de regressão entre dureza e resistência Rockwell, todos têm uma significância P menor que 0,05 e uma qualidade de ajuste próxima R2.
Dado que a relação de conversão entre a dureza Rockwell e a resistência à tração do aço de baixo carbono especificada na norma é semelhante ao modelo polinomial, recomenda-se a utilização do modelo quadrático para conversão.
A fórmula após o ajuste é:
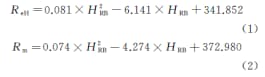
Onde: REh é o limite de escoamento superior; Reu é a resistência à tração; HRB é a dureza Rockwell.
2.1.2 Análise de desvio relativo dos resultados de conversão
Com base no modelo de regressão quadrática ajustado, os desvios relativos entre os valores convertidos do limite superior de escoamento e da resistência à tração e os resultados do ensaio de tração foram calculados e analisados estatisticamente. O tamanho da amostra foi de 162 e os resultados são apresentados na Tabela 3.
Os desvios relativos seguem uma distribuição normal, e a distribuição de frequência é mostrada na Figura 3.
Tabela 3 Tabela Estatística de Desvio Relativo da Dureza Rockwell à Resistência
| Itens estatísticos | Valor mínimo | Máximo | Desvio médio | Referência padrão |
| Desvio relativo do valor de conversão do limite de escoamento superior | -16,56 | +16,61 | ±5,46 | 6,84 |
| Desvio relativo da resistência à tração convertida | -13h31 | +11.16 | ±4,12 | 5.03 |
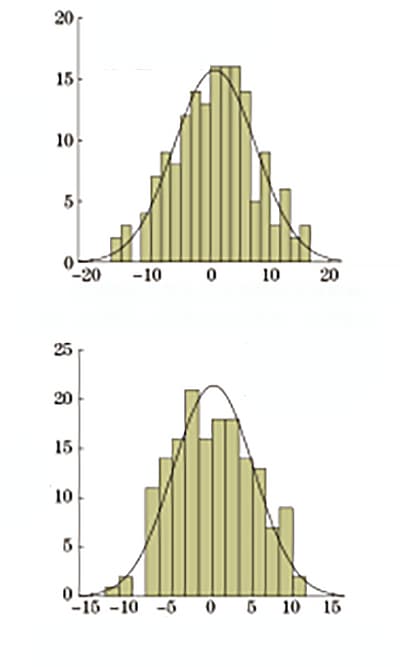
Fig. 3 Desvio relativo da dureza Rockwell em relação à resistência
2.1.3 Comparação com valor de conversão padrão nacional
A Figura 4 mostra uma comparação do valor de conversão da resistência à tração especificada no padrão, o valor de conversão da fórmula de regressão quadrática ajustada e o gráfico de dispersão da relação correspondente entre a dureza Rockwell e a resistência à tração, todos no mesmo gráfico.
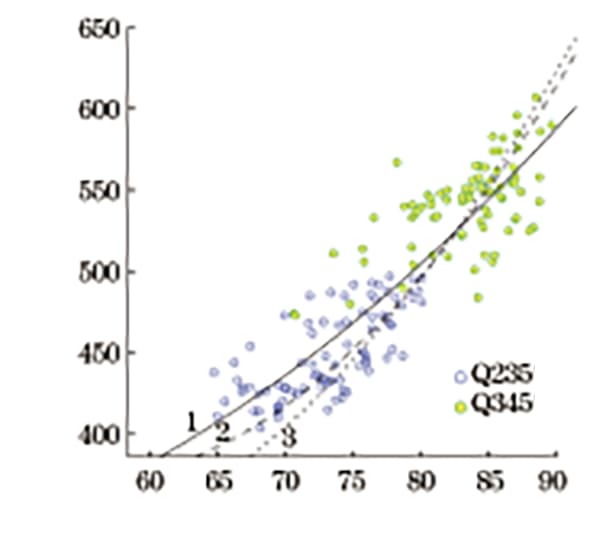
Fig. 4 Gráfico de comparação de resistência à tração convertida pela dureza Rockwell
Conforme observado na Figura 4, a tendência geral das três curvas é consistente. O valor de conversão da resistência à tração dado em GB/T 1172-1999 é semelhante ao do autor, com desvio médio de 2,7% e desvio máximo de 5,7% na faixa de 370 a 630 MPa.
No entanto, o valor de conversão da resistência à tração dado em GB/T 33362-2016 é menor para o aço Q235 (com resistência à tração na faixa de 370 a 500 MPa) e maior para o aço Q345 (com resistência à tração na faixa de 470 a 630 MPa).
2.2 Correlação entre dureza e resistência Vickers
2.2.1 Processo de teste de dureza Vickers e análise de resultados
A superfície da amostra foi polida com uma esmerilhadeira e o instrumento foi calibrado com um bloco de dureza padrão. O teste de dureza Vickers foi realizado de acordo com os requisitos do teste de dureza Vickers de materiais metálicos GB/T 4340.1-2009, parte 1: método de teste. Foram medidos três pontos para cada amostra e obtido o valor médio.
O software SPSS foi utilizado para realizar regressão linear, regressão quadrática, regressão de potência e análise de regressão exponencial na dureza Vickers, limite de escoamento superior e resistência à tração. O diagrama de análise de regressão está representado na Figura 5, e os resultados da análise de regressão são apresentados na Tabela 4 e na Tabela 5.
Tabela 4 Dados do modelo de regressão de dureza Vickers e limite de escoamento superior
| Equação | Resumo do modelo | Parâmetro do modelo | ||||
| R2 | F | Significância P | constante | b1 | b2 | |
| Expoente quadrático linear | 0,727 | 426.980 | 0,000 | -9.332 | 2.530 | 0,002 |
| 0,728 | 212.272 | 0,000 | 27.358 | 2.020 | ||
| 0,731 | 433.768 | 0,000 | 2.215 | 1.021 | ||
| 0,731 | 435.083 | 0,000 | 126.740 | 0,007 | ||
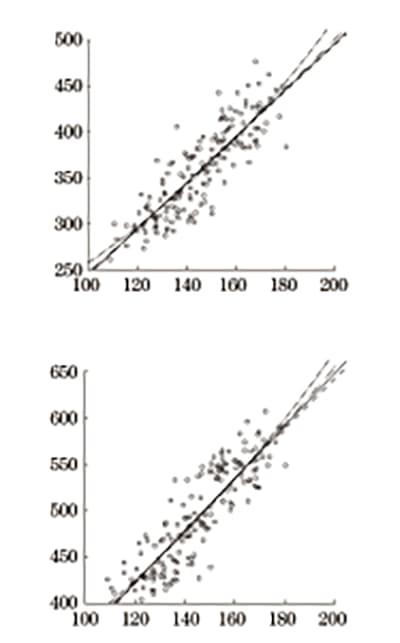
Fig. 5 Análise de regressão da dureza e resistência Vickers
Tabela 5 Dados do Modelo de Regressão de Dureza Vickers e Resistência à Tração
| Equação | Resumo do modelo | Parâmetro do modelo | ||||
| R2 | F | Significância P | Constante | b1 | b2 | |
| Expoente quadrático linear | 0,753 | 486.507 | 0,000 | 84.099 | 2.818 | 0,002 |
| 0,753 | 241.944 | 0,000 | 133.182 | 2.136 | ||
| 0,748 | 475.262 | 0,000 | 8.189 | 0,823 | ||
| 0,751 | 483.330 | 0,000 | 213.597 | 0,006 | ||
Conforme indicado pela Tabela 4 e Tabela 5, a dureza Vickers tem uma forte correlação com a resistência, e a correlação com a resistência à tração é mais forte em comparação com a resistência ao escoamento superior.
Dos quatro modelos de regressão entre dureza e resistência Vickers, todos têm uma significância P menor que 0,05 e uma qualidade de ajuste próxima R2.
Dado que a relação de conversão entre a dureza Vickers e a resistência à tração do aço de baixo carbono especificada na norma é próxima de uma relação linear, recomenda-se utilizar a relação linear para conversão.
A fórmula após o ajuste é:
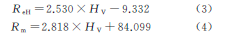
Onde: HV é a dureza Vickers.
2.2.2 Análise de desvio relativo dos resultados de conversão
Com base no modelo de regressão linear ajustado, os desvios relativos entre os valores convertidos do limite superior de escoamento e da resistência à tração e os resultados do ensaio de tração foram calculados e analisados estatisticamente. O tamanho da amostra foi de 162 e os resultados são apresentados na Tabela 6.
Os desvios relativos seguem uma distribuição normal, e a distribuição de frequência é mostrada na Figura 6.
Tabela 6 Tabela Estatística de Desvio Relativo da Dureza Vickers para Resistência
| Itens estatísticos | Valor mínimo | Máximo | Desvio médio | Referência padrão |
| Desvio relativo do valor de conversão do limite de escoamento superior | -19h30 | +17,55 | ±5,75 | 7.09 |
| Desvio relativo da resistência à tração convertida | -12h32 | +15,83 | ±4,88 | 5,44 |
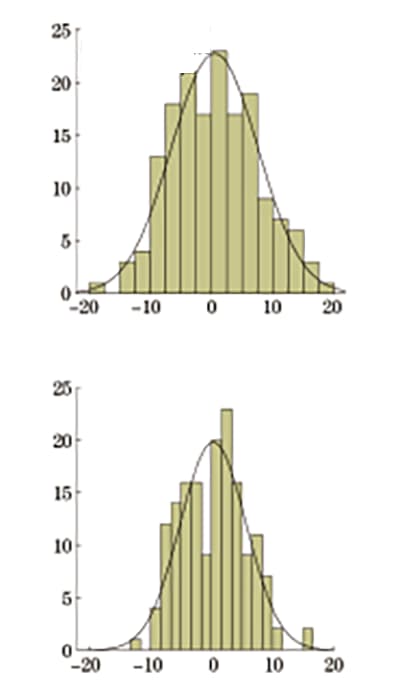
Fig. 6 Desvio relativo da dureza Vickers convertido em resistência
2.2.3 Comparação com valor de conversão padrão nacional
A Figura 7 mostra uma comparação do valor de conversão da resistência à tração especificada na norma, o valor de conversão da fórmula de regressão linear obtida pelo autor e o gráfico de dispersão da relação correspondente entre dureza Vickers e resistência à tração, todos no mesmo gráfico .
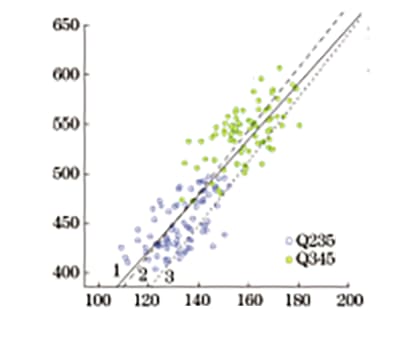
Fig. 7 Gráfico de comparação da resistência à tração convertida pela dureza Vickers
Conforme observado na Figura 7, a tendência geral das três curvas é consistente. O valor de conversão da resistência à tração especificado em GB/T 1172-1999 é muito próximo do valor de conversão obtido pelo autor. Na faixa de 370 a 630 MPa, a diferença entre eles aumenta ligeiramente com o aumento do valor de dureza, com desvio médio de 1,2% e desvio máximo de 3,3%. No entanto, o valor de conversão da resistência à tração fornecido em GB/T 33362-2016 é geralmente menor.
2.3 Correlação entre dureza e resistência Brinell
2.3.1 Processo de teste de dureza Brinell e análise de resultados
A superfície da amostra foi polida com uma esmerilhadeira para garantir uma rugosidade superficial não superior a 1,6 μm. O instrumento foi calibrado com um bloco de dureza padrão e o teste de dureza Brinell foi realizado de acordo com os requisitos do GB/T 231.1-2018 Teste de dureza Brinell de materiais metálicos Parte 1: Método de teste. Foi utilizado um penetrador de metal duro com diâmetro de 10 mm e a força de ensaio foi de 29,42 kN. Foram medidos três pontos para cada amostra e obtido o valor médio.
O software SPSS foi utilizado para realizar regressão linear, regressão quadrática, regressão de potência e análise de regressão exponencial na dureza Brinell, limite de escoamento superior e resistência à tração. O diagrama de análise de regressão está representado na Figura 8, e os resultados da análise de regressão são apresentados na Tabela 7 e na Tabela 8.
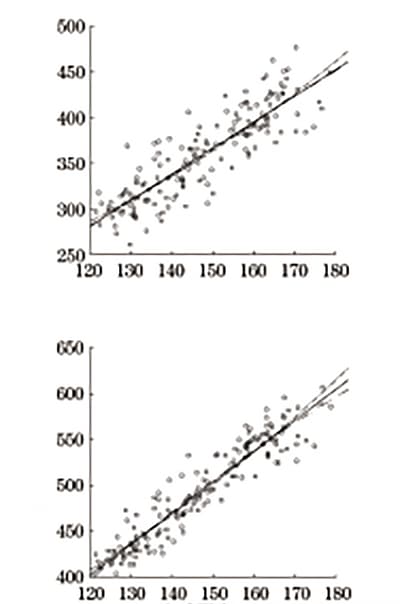
Fig. 8 Análise de regressão da dureza e resistência Brinell
Tabela 7 Dados do modelo de regressão de dureza Brinell e limite de escoamento superior
| Equação | Resumo do modelo | Parâmetro do modelo | ||||
| R2 | F | Significância P | constante | b1 | b2 | |
| Expoente quadrático linear | 0,756 | 495.403 | 0,000 | -59.965 | 2.846 | -0,001 |
| 0,758 | 246.186 | 0,000 | -86.188 | 3.205 | ||
| 0,757 | 497.365 | 0,000 | 1.048 | 1.168 | ||
| 0,756 | 494.881 | 0,000 | 110.318 | 0,008 | ||
Tabela 8 Dados do modelo de regressão de dureza Brinell e resistência à tração
| Equação | Resumo do modelo | Parâmetro do modelo | ||||
| R2 | F | Significância P | constante | b1 | b2 | |
| Expoente quadrático linear | 0,887 | 1253.313 | 0,000 | -2,613 | 3.377 | -0,001 |
| 0,888 | 631.852 | 0,000 | -225.666 | 6.424 | ||
| 0,889 | 1286.205 | 0,000 | 3.204 | 1.009 | ||
| 0,886 | 1238.834 | 0,000 | 179.073 | 0,007 | ||
Conforme indicado pela Tabela 7 e Tabela 8, a dureza Brinell tem uma forte correlação com a resistência, e a correlação com a resistência à tração é mais forte em comparação com a resistência ao escoamento superior.
Dos quatro modelos de regressão entre dureza e resistência Brinell, todos têm uma significância P menor que 0,05 e uma qualidade de ajuste próxima R2.
Dado que a relação de conversão entre a dureza Brinell do aço carbono e a resistência à tração especificada na norma é próxima de uma relação linear, recomenda-se usar uma relação linear para conversão.
A fórmula ajustada é:
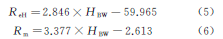
Onde: HPN é a dureza Brinell.
2.3.2 Análise de desvio relativo dos resultados de conversão
De acordo com o modelo de regressão linear ajustado, os desvios relativos entre os valores convertidos do limite de escoamento superior e da resistência à tração e os resultados do teste de tração são calculados respectivamente, e os desvios relativos são analisados estatisticamente.
As estatísticas são 162 e os resultados são mostrados na Tabela 9.
Os desvios relativos são basicamente distribuição normal, e a distribuição de frequência é mostrada na Fig.
Tabela 9 Tabela Estatística de Desvio Relativo da Dureza Brinell à Resistência
| Itens estatísticos | Valor mínimo | Máximo | Desvio médio | Referência padrão |
| Desvio relativo do valor de conversão do limite de escoamento superior | -16,78 | +18,67 | ±5,38 | 6,75 |
| Desvio relativo da resistência à tração convertida | -9,25 | +8,55 | ±2,89 | 3,59 |
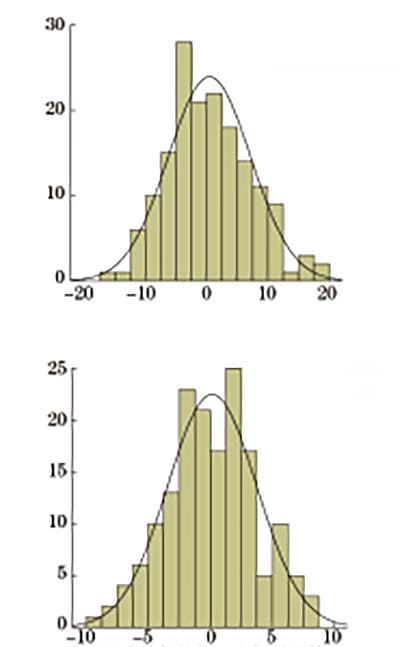
Fig. 9 Desvio relativo da dureza Brinell convertido em resistência
2.3.3 Comparação com valor de conversão padrão nacional
Na norma GB/T 1172-1999, a relação entre a força de teste e o diâmetro da esfera do penetrador do teste de dureza Brinell é 10.
O teste do autor é realizado de acordo com GB/T 231.1-2018. Com referência às disposições da norma, a relação entre a força de teste e o diâmetro da esfera do penetrador é 30.
Portanto, não é mais comparado com GB/T 1172-1999 em comparação com o valor de conversão do padrão nacional.
O valor de conversão padrão da resistência à tração fornecido em GB/T 33362-2016, o valor de conversão da fórmula de regressão linear ajustada pelo autor e o gráfico de dispersão da relação correspondente entre a dureza Brinell e a resistência à tração são comparados no mesmo gráfico, conforme mostrado na Figura 10.
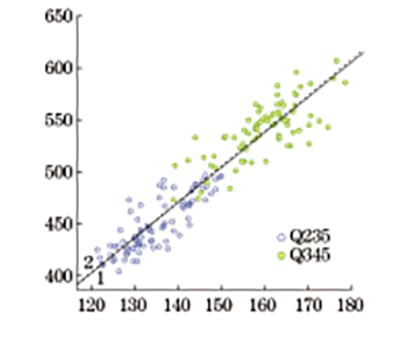
Fig. 10 Gráfico de comparação de resistência à tração convertida pela dureza Brinell
Pode-se observar na Figura 10 que o valor de conversão da resistência à tração dado em GB/T 33362-2016 quase coincide com a curva de regressão da resistência à tração ajustada pelo autor, com um desvio médio de 0,4% e um desvio máximo de 1,2 % dentro de 370-630MPa.
Nos últimos anos, o rápido desenvolvimento de vários testadores de dureza portáteis trouxe grande conveniência aos testes no local.
Atualmente, muitos tipos de testador de dureza Rockwell portátil e testador de dureza Brinell portátil podem ser adquiridos no mercado.
O equipamento é portátil, simples de operar, rápido de medir e a precisão da detecção também atende aos requisitos das normas nacionais, o que é adequado para detecção de engenharia no local.
Existem também vários equipamentos de processamento portáteis para tratamento de superfície de amostras, que podem atender aos requisitos de teste.
Portanto, é viável utilizar a dureza Rockwell e a dureza Brinell para calcular a resistência do aço na inspeção de campo de estruturas de aço.
3. Conversão de dureza em resistência para metais ferrosos (GB/T 1172-1999)
| Dureza | Resistência à tracção σb/MPa |
||||||||||||||||
| Rockwell | Superfície Rockwell | Vickers | Brinell | Aço carbono | Aço cromo | Aço cromo bário | Aço cromo níquel | Aço cromo molibdênio | Aço cromo níquel molibdênio | Aço cromo-manganês-silício | Aço de ultra-alta resistência | Aço inoxidável | Nenhum tipo específico de aço especificado | ||||
| CDH | RH | HR15N | HR30N | HR45N | Alta tensão | HB30D2 |
d10.2d5.4d2,5 /milímetros |
||||||||||
| 17 | – | 67,3 | 37,9 | 15.6 | 211 | 211 | 4.15 | 73,6 | 706 | 705 | 772 | 726 | – | 757 | – | 703 | 724 |
| 18 | – | 67,8 | 38,9 | 16,8 | 216 | 216 | 4.11 | 753 | 723 | 719 | 779 | 737 | – | 769 | – | 719 | 737 |
| 19 | – | 68,3 | 39,8 | 18 | 221 | 220 | 4.07 | 771 | 739 | 735 | 788 | 749 | – | 782 | – | 737 | 752 |
| 20 | – | 68,8 | 40,7 | 19.2 | 226 | 225 | 4.03 | 790 | 757 | 751 | 797 | 761 | – | 796 | – | 754 | 767 |
| 21 | – | 69,3 | 41,7 | 20.4 | 231 | 227 | 4 | 809 | 775 | 767 | 807 | 775 | – | 810 | – | 773 | 782 |
| 22 | – | 69,8 | 42,6 | 21,5 | 237 | 234 | 3,95 | 829 | 794 | 785 | 819 | 789 | – | 825 | – | 792 | 799 |
| 23 | – | 70,3 | 43,6 | 22,7 | 243 | 240 | 3,91 | 849 | 814 | 803 | 831 | 805 | – | 840 | – | 812 | 816 |
| 24 | – | 70,8 | 44,5 | 23,9 | 249 | 245 | 3,87 | 870 | 834 | 823 | 845 | 821 | – | 856 | – | 832 | 835 |
| 25 | – | 71,4 | 45,5 | 25.1 | 255 | 251 | 3,83 | 892 | 855 | 843 | 860 | 838 | – | 874 | – | 853 | 854 |
| 26 | – | 71,9 | 46,4 | 26.3 | 261 | 257 | 3,78 | 914 | 876 | 864 | 876 | 857 | 876 | 892 | – | 875 | 874 |
| 27 | – | 72,4 | 47,3 | 27,5 | 268 | 263 | 3,74 | 937 | 898 | 886 | 893 | 877 | 897 | 910 | – | 897 | 895 |
| 28 | – | 73 | 48,3 | 28,7 | 274 | 269 | 3.7 | 961 | 920 | 909 | 912 | 897 | 918 | 930 | – | 919 | 917 |
| 29 | – | 73,5 | 49,2 | 29,9 | 281 | 276 | 3,65 | 984 | 943 | 933 | 932 | 919 | 941 | 951 | – | 942 | 940 |
| 30 | – | 74,1 | 50,2 | 31.1 | 289 | 283 | 3,61 | 1009 | 967 | 959 | 953 | 943 | 966 | 973 | – | 966 | 904 |
| 31 | – | 74,7 | 51.1 | 32,3 | 296 | 291 | 3,56 | 1034 | 991 | 985 | 976 | 967 | 991 | 996 | – | 990 | 989 |
| 32 | – | 75,2 | 52 | 33,5 | 304 | 298 | 3,52 | 1060 | 1016 | 1013 | 1001 | 993 | 1018 | 1020 | – | 1015 | 1015 |
| 33 | – | 75,8 | 53 | 34,7 | 312 | 306 | 3,48 | 1086 | 1042 | 1042 | 1027 | 1020 | 1047 | 1046 | – | 1041 | 1042 |
| 34 | – | 76,4 | 53,9 | 25,9 | 320 | 314 | 3,43 | 1113 | 1068 | 1072 | 1054 | 1049 | 1077 | 1073 | – | 1067 | 1070 |
| 35 | – | 77 | 54,8 | 37 | 329 | 323 | 3,39 | 1141 | 1095 | 1104 | 1084 | 1079 | 1108 | 1101 | – | 1095 | 1100 |
| 36 | – | 77,5 | 55,8 | 38,2 | 338 | 332 | 3,34 | 1170 | 1124 | 1136 | 1115 | 1111 | 1141 | 1130 | – | 1126 | 1131 |
| 37 | – | 78,1 | 56,7 | 39,4 | 347 | 341 | 3.3 | 1200 | 1153 | 1171 | 1148 | 1144 | 1176 | 1161 | – | 1153 | 1163 |
| 38 | – | 78,7 | 57,6 | 40,6 | 357 | 350 | 3.26 | 1231 | 1184 | 1206 | 1132 | 1179 | 1212 | 1194 | – | 1184 | 1197 |
| 39 | 70 | 79,3 | 58,6 | 41,8 | 367 | 360 | 3.21 | 1263 | 1216 | 1243 | 1219 | 1216 | 1250 | 1228 | 1218 | 1216 | 1232 |
| 40 | 70,5 | 79,9 | 59,5 | 43 | 377 | 370 | 3.17 | 1296 | 1249 | 1282 | 1257 | 1254 | 1290 | 1264 | 1267 | 1250 | 1268 |
| 41 | 71,1 | 80,5 | 60,4 | 44,2 | 388 | 380 | 3.13 | 1331 | 1284 | 1322 | 1298 | 1294 | 1331 | 1302 | 1315 | 1286 | 1307 |
| 42 | 71,6 | 81,1 | 61,3 | 45,4 | 399 | 391 | 3.09 | 1367 | 1322 | 1364 | 1340 | 1336 | 1375 | 1342 | 1362 | 1325 | 1347 |
| 43 | 72,1 | 81,7 | 62,3 | 46,5 | 411 | 401 | 3.05 | 1405 | 1361 | 1407 | 1385 | 1379 | 1420 | 1384 | 1409 | 1366 | 1389 |
| 44 | 72,6 | 82,3 | 63,2 | 47,7 | 423 | 413 | 3.01 | 1445 | 1403 | 1452 | 1431 | 1425 | 1467 | 1427 | 1455 | 1410 | 1434 |
| 45 | 73,2 | 82,9 | 64,1 | 48,9 | 436 | 424 | 2,97 | 1488 | 1448 | 1498 | 1480 | 1472 | 1516 | 1474 | 1502 | 1457 | 1480 |
| 46 | 73,7 | 83,5 | 65 | 50,1 | 449 | 436 | 2,93 | 1533 | 1497 | 1547 | 1531 | 1522 | 1567 | 1522 | 1550 | 1508 | 1529 |
| 47 | 74,2 | 84 | 65,9 | 51.2 | 462 | 449 | 2,89 | 1581 | 1549 | 1597 | 1584 | 1573 | 1620 | 1573 | 1600 | 1563 | 1581 |
| 48 | 74,7 | 84,6 | 66,8 | 52,4 | 478 | 401 | 2,85 | 1631 | 1605 | 1649 | 1640 | 1626 | 1676 | 1627 | 1652 | 1623 | 1635 |
| 49 | 75,3 | 85,2 | 67,7 | 53,6 | 493 | 474 | 2,81 | 1686 | 1666 | 1702 | 1698 | 1682 | 1733 | 1683 | 1707 | 1688 | 1692 |
| 50 | 75,8 | 85,7 | 68,6 | 54,7 | 509 | 488 | 2,77 | 1744 | 1731 | 1758 | 1758 | 1739 | 1793 | 1742 | 1765 | 1759 | 1753 |
| 51 | 76,3 | 86,3 | 69,5 | 55,9 | 525 | 501 | 2,73 | – | 1803 | 1816 | 1821 | 1799 | 1854 | 1804 | 1827 | – | 1817 |
| 52 | 76,9 | 86,8 | 70,4 | 57.1 | 543 | – | – | – | 1881 | 1875 | 1887 | 1861 | 1918 | 1870 | 1894 | – | 1885 |
| 53 | 77,4 | 87,4 | 71,3 | 58,2 | 561 | – | – | – | – | 1937 | 1955 | 1925 | 1985 | 1938 | 1967 | – | 1957 |
| 54 | 77,9 | 87,9 | 72,2 | 59,4 | 579 | – | – | – | – | 2000 | 2025 | – | – | 2010 | 2045 | – | 2034 |
| 55 | 78,5 | 88,4 | 73,1 | 60,5 | 599 | – | – | – | – | 2066 | 2098 | – | – | 2086 | 2131 | – | 2115 |
| 56 | 79 | 88,9 | 73,9 | 61,7 | 620 | – | – | – | – | – | – | – | – | – | 2224 | – | 2201 |
| 57 | 79,5 | 89,4 | 74,8 | 62,8 | 642 | – | – | – | – | – | – | – | – | – | 2324 | – | 2293 |
| 58 | 80,1 | 89,8 | 75,6 | 63,9 | 664 | – | – | – | – | – | – | – | – | – | 2437 | – | 2391 |
| 59 | 80,6 | 90,2 | 76,5 | 65,1 | 688 | – | – | – | – | – | – | – | – | – | 2558 | – | 2496 |
| 60 | 81,2 | 90,6 | 77,3 | 66,2 | 713 | – | – | – | – | – | – | – | – | – | 2691 | – | 2607 |
| 61 | 81,7 | 91 | 78,1 | 67,3 | 739 | – | – | – | – | – | – | – | – | – | – | – | – |
| 62 | 82,2 | 91,4 | 79 | 68,4 | 766 | – | – | – | – | – | – | – | – | – | – | – | – |
| 63 | 82,8 | 91,7 | 79,8 | 69,5 | 795 | – | – | – | – | – | – | – | – | – | – | – | – |
| 64 | 83,3 | 91,9 | 80,6 | 70,6 | 825 | – | – | – | – | – | – | – | – | – | – | – | – |
| 65 | 83,9 | 92,2 | 81,3 | 71,7 | 856 | – | – | – | – | – | – | – | – | – | – | – | – |
| 66 | 84,4 | – | – | – | 889 | – | – | – | – | – | – | – | – | – | – | – | – |
| 67 | 85 | – | – | – | 923 | – | – | – | – | – | – | – | – | – | – | – | – |
| 68 | 85,5 | – | – | – | 959 | – | – | – | – | – | – | – | – | – | – | – | – |
| 69 | 86,1 | – | – | – | 997 | – | – | – | – | – | – | – | – | – | – | – | – |
| 70 | 86,6 | – | – | – | 1037 | – | – | – | – | – | – | – | – | – | – | – | – |
3. Conclusão
(1) A dureza Rockwell, a dureza Vickers e a dureza Brinell apresentam boa correlação com a resistência. Com base no teste do material, a fórmula de conversão da dureza Rockwell, dureza Vickers e dureza e resistência Brinell é obtida, e o desvio relativo da conversão está dentro da faixa permitida do projeto.
O desvio relativo entre a dureza Brinell e a resistência à tração é obviamente menor do que a dureza Rockwell e a dureza Vickers.
(2) A resistência à tração convertida da dureza Rockwell fornecida em GB/T 33362-2016 é baixa para o aço Q235 e alta para o aço Q345.
A resistência à tração convertida da dureza Vickers é ligeiramente menor.
A resistência à tração convertida da dureza Brinell é consistente com os resultados do teste.
Os valores de resistência à tração convertidos pela dureza Rockwell e dureza Vickers dados em GB/T 1172-1999 estão próximos dos resultados do teste.
(3) Combinado com os instrumentos portáteis de teste de dureza existentes e equipamentos de processamento de amostras, o uso da dureza Rockwell e da dureza Brinell para calcular a resistência do aço é operável em projetos práticos e pode ser aplicado à prática de engenharia.