O magnetismo tem sido uma força fascinante desde os tempos antigos. As primeiras civilizações eram fascinadas pelas propriedades dos magnetos e usavam bússolas magnéticas para navegação. Mas foi só no século XVI que William Gilbert estabeleceu o magnetismo como uma ciência com o seu trabalho pioneiro. Seu influente livro “De Magnete” lançou as bases para a compreensão do campo magnético e seu comportamento. Desde então, o estudo do magnetismo evoluiu, levando à descoberta de leis e princípios fundamentais que regem os circuitos magnéticos e sua aplicação em diversos avanços tecnológicos.
Cálculos de circuito magnético
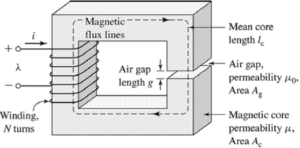
O circuito magnético forma a espinha dorsal de vários dispositivos elétricos e eletrônicos e permite a transmissão e uso eficiente de energia magnética. Decifrar as leis fundamentais que regem o circuito magnético é crucial para compreender e otimizar esses sistemas. Descobriu-se que as leis que regem o fluxo constante de corrente num curso podem ser facilmente alteradas. Para ser imediatamente aplicável ao Circuito magnético. Portanto
Força motriz magnetomotriz = fluxo x relutância
F = ΦxS
Corresponde exatamente à força eletromotriz = corrente x resistência
Relutância = (Comprimento/Área) x (1/Permeabilidade)
= l/Aµ
Para um ímã com área de seção transversal uniforme que corresponda exatamente
Resistência = (Comprimento/Área) x (1/Condutividade)
Muitas vezes é conveniente calcular em dimensões unitárias. Temos então
mmf por unidade de comprimento = fluxo x relutância por unidade de comprimento
= (fluxo/área) x (l/permeabilidade)
= densidade de fluxo x (l/permeabilidade)
Intensidade do campo magnético H = B/µ
Isto corresponde exatamente a
Para um material com fluxo uniformemente distribuído e comprimento l, a FMM total é igual à FMM por unidade de comprimento xl
ou seja, F=Hl ou AT=Hl
Por lidar com o Circuito magnético onde o fluxo deve passar por diversas partes diferentes em segundos, os métodos usados para lidar com circuitos elétricos em série podem ser aplicados imediatamente, sendo a relutância total a soma dos valores das diferentes partes. Normalmente, a importância da relutância só é significativa na medida em que permite determinar a FMM necessária para produzir um determinado fluxo no circuito. O método mais simples geralmente é determinar esse valor de FMM total adicionando os valores de FMM necessários para produzir o fluxo através das várias partes do circuito. Isto é exatamente o mesmo que calcular a queda de tensão total em um circuito elétrico somando os valores da queda de tensão nas diferentes partes.
Assim, o valor total da FMM em torno de um campo magnético completo é dado por
AT (ou) F = ∫Hdl
Ou se o circuito consistir em várias partes homogêneas, cada uma das quais com seção transversal e comprimento uniformes1EU2 etc.
FMM total F (ou) AT = Σ Hl = H111 +H2eu2 +….
= Φ (p1 +S2 +….)
Se os valores da área e permeabilidade das diferentes partes dos circuitos são A1μ1etc. torna-se todo o MMF
AT (ou) F = (B1/μ1)eu1 + (B2/μ2)eu2 +…..
Onde B1 =Φ/UMA1 etc.
Ocasionalmente é conveniente expressar a lei básica do circuito magnético na forma.
Fluxo = força magnetomotriz x permeância
Permeabilidade nada mais é do que a recíproca de Restrição tratar caminhos em paralelo; a permeância total é a soma dos valores dos caminhos individuais.
A principal diferença entre os cálculos elétricos e magnéticos surge do fato de que a resistência de um circuito elétrico não depende diretamente do valor da relutância de uma substância magnética, mas em grande medida do valor do fluxo que passa por ela.
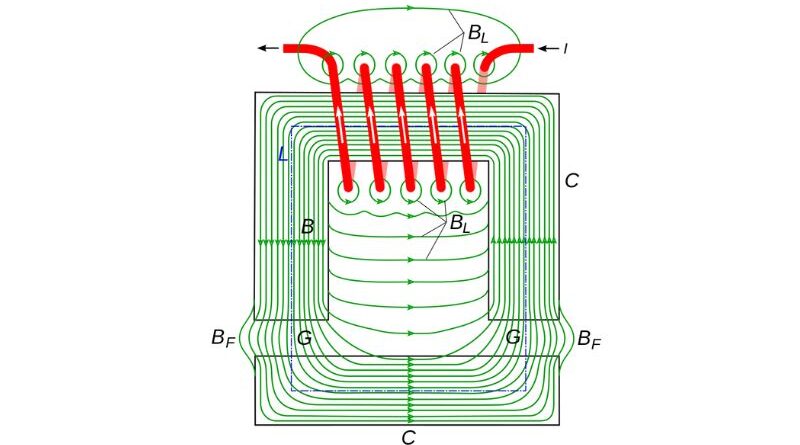
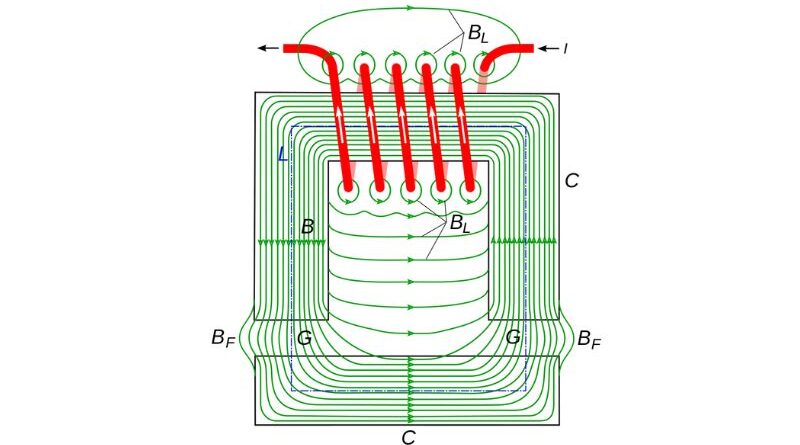
O campo magnético e o fluxo magnético
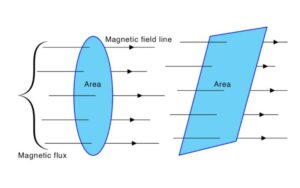
Compreender o campo magnético é crucial para compreender como os ímãs interagem entre si e com outros objetos. O conceito de campo magnético é representado visualmente pelas linhas de força de Faraday, que indicam a direção e a força do campo magnético. O fluxo magnético, a medida de um campo magnético que passa por uma superfície, é fundamental para a compreensão das interações magnéticas. O cálculo do fluxo magnético é essencial para diversas aplicações, principalmente em circuitos magnéticos e transformadores.
Lei de circulação de Ampère
As contribuições de André-Marie Ampère revolucionaram a compreensão do eletromagnetismo. Seus experimentos com condutores condutores de corrente levaram à formulação da lei do circuito de Ampère, que estabelece a relação entre campos magnéticos e correntes elétricas. A lei fornece uma ferramenta fundamental para analisar circuitos magnéticos e calcular o campo magnético gerado por condutores que transportam corrente. A lei do circuito de Ampère lançou as bases para avanços futuros no eletromagnetismo.
Indução magnética e lei de Faraday
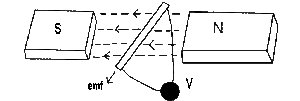
Os experimentos inovadores de Michael Faraday sobre indução eletromagnética marcaram uma virada no eletromagnetismo. A lei de Faraday afirma que um campo magnético variável induz uma força eletromotriz (EMF) em um condutor. Essa descoberta abriu caminho para o desenvolvimento de componentes indutivos, como transformadores e indutores, essenciais nos sistemas elétricos modernos.
A curva BH e histerese
A curva BH representa a relação entre a indução magnética (B) e a intensidade do campo magnético (H) em um material magnético. Compreender a curva BH é importante para prever o comportamento de materiais magnéticos sob campos magnéticos variados. Histerese refere-se ao fenômeno de que um material magnético retém magnetismo residual mesmo após o campo magnético aplicado ser removido. Este comportamento leva a perdas de energia em circuitos magnéticos e minimizar os efeitos de histerese é crucial para uma operação eficiente.
Análise de circuito magnético
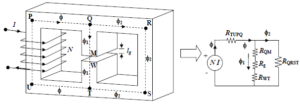
Os circuitos magnéticos podem ser analisados usando princípios semelhantes aos dos circuitos elétricos. Os modelos e cursos correspondentes simplificam sistemas magnéticos complexos e facilitam o estudo e a compreensão do seu comportamento. Parâmetros como intensidade do campo magnético, fluxo magnético e resistência magnética são calculados para avaliar e otimizar circuitos magnéticos. As leis de Kirchhoff, adotadas a partir da análise de circuitos elétricos, são aplicadas a circuitos magnéticos para resolver problemas práticos.
Aplicações de circuitos magnéticos
Os circuitos magnéticos têm uma ampla gama de aplicações na tecnologia moderna. Motores e geradores elétricos utilizam circuitos magnéticos para converter energia elétrica em trabalho mecânico e vice-versa. Sensores magnéticos usam princípios como o efeito Hall e encontram aplicações em diversos setores, incluindo automotivo, médico e eletrônico de consumo. A blindagem magnética é essencial para proteger dispositivos eletrônicos sensíveis contra interferência eletromagnética (EMI) causada por campos magnéticos externos.