1. O que é tensão? O que é microtensão? Qual é a unidade de deformação?

Primeiro, a maior parte da indústria de monitoramento de segurança mede a deformação da estrutura que está sendo testada. Muita deformação pode causar acidentes.
Por exemplo, fissuras em estruturas, afundamentos e deslocamentos entre a estrutura e uma referência fixa, são grandes deformações que podem ser vistas a olho nu, e podem ser medidas em milímetros usando medidores como medidores de fissuras, níveis estáticos e deslocamentos. Manômetros.
Mas como pode ser representada a pequena deformação causada pela compressão dentro da estrutura que está sendo testada ou pela flexão fora do objeto em forma de viga?
A resposta é tensão.

Suponha que o comprimento de uma estrutura com comprimento L sofra deformação sob tensão e seu comprimento mude para L', então sua mudança no comprimento ΔL = L' – L, e a deformação ε é a razão entre a mudança no comprimento ΔL e o comprimento original L, a fórmula é a seguinte:

Então, qual é a unidade de deformação?
Como pode ser visto na fórmula, a deformação é uma razão e não tem dimensão, o que significa que não tem unidade.
Então, o que é microtensão?
Como ΔL é muito pequeno, geralmente na faixa de mícrons, o valor de deformação calculado é muito pequeno, com muitas casas decimais, tornando-o inconveniente para exibição e visualização, então é introduzida a notação científica 10-6, chamada microdeformação με, que pode ser entendido como a unidade de microdeformação é 10-6, e nossa faixa de medição de extensômetro é de ± 1500 microdeformações, positivo indicando alongamento e negativo indicando compressão.
2. O que é estresse? Qual é a relação entre tensão e estresse? Como a deformação calcula o estresse?
A deformação é uma pequena deformação dentro da estrutura que está sendo testada, então por que ela se deforma? Porque está sujeito a forças externas.
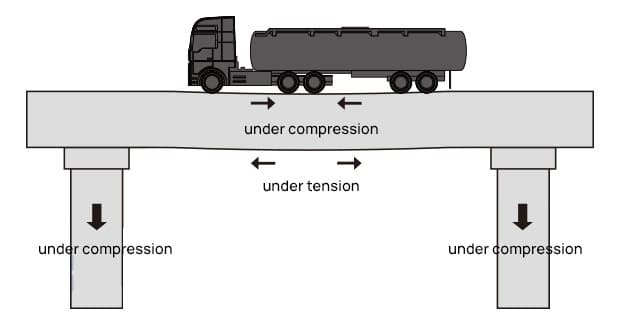
Tomando como exemplo o píer de uma ponte, se um caminhão totalmente carregado passar pela ponte, o píer suportará pressão adicional e produzirá compressão e deformação de compressão, enquanto o píer produzirá uma força interna para neutralizar a força externa e superar a deformação.
Essa força interna é o estresse. A tensão é definida como a força por unidade de área, que na verdade é pressão, com unidades de MPa.
Então, qual é a relação entre a variável deformação e a mudança na tensão suportada? Veja a fórmula de cálculo:

Na fórmula, σ representa a tensão, E é o módulo de elasticidade do material que está sendo testado, também conhecido como módulo de Young, que é uma quantidade física que descreve a elasticidade do material.
Pode ser visto como a capacidade do material de resistir à deformação (rigidez) e, de uma perspectiva micro, é a força de ligação entre átomos e moléculas.
Dois materiais com a mesma deformação (o mesmo valor de deformação), o material com maior resistência à deformação (um módulo de elasticidade maior) suportará uma tensão maior.
Por exemplo, tofu e bloco de ferro do mesmo tamanho, se sua altura for comprimida em 1 mm, o primeiro só precisa ser pressionado suavemente com a mão, enquanto o segundo deve ser auxiliado por uma ferramenta.
O módulo de elasticidade de materiais de engenharia comuns pode ser encontrado em tabelas, como o módulo de elasticidade do concreto C30 é 30000MPa (1N/mm2 = 1MPa), e o módulo de elasticidade do aço carbono é 206GPa.
O módulo de elasticidade Ec do concreto sob compressão e tração deverá ser adotado conforme Tabela 4.1.5.
O módulo de deformação por cisalhamento Gc do concreto pode ser adotado em 40% do valor do módulo de elasticidade correspondente.
O coeficiente de Poisson Vc do concreto pode ser adotado em 0,2.
Tabela 4.15 Módulo de elasticidade do concreto (×104N/mm2).
| Grau de resistência do concreto | C15 | C20 | C25 | C30 | C35 | C40 | C45 | C50 | Capítulo 55 | C60 | C65 | C70 | C75 | C80 |
| CE | 2.20 | 2,55 | 2,80 | 3h00 | 3.15 | 3,25 | 3,35 | 3,45 | 3,55 | 3,60 | 3,65 | 3,70 | 3,75 | 3,80 |
Observação:
1. Quando dados de teste confiáveis estão disponíveis, o módulo de elasticidade pode ser determinado com base em dados medidos reais;
2. Quando uma grande quantidade de aditivos minerais é adicionada ao concreto, o módulo de elasticidade pode ser determinado com base em dados reais medidos de acordo com a idade especificada.
Tabela 1.1-13 Módulo de elasticidade e razão de Poisson de materiais comumente usados
| Item | Módulo elástico E/GPa |
Módulo de cisalhamento G/GPa |
Razão de Poisson μ |
Item | Módulo elástico E/GPa |
Módulo de cisalhamento G/GPa |
Teflon |
| ferro fundido cinzento | 118~126 | 44,3 | 0,3 | Zinco laminado | 82 | 31.4 | 0,27 |
| Ferro fundido nodular | 173 | 0,3 | Liderar | 16 | 6.8 | 0,42 | |
| Aço carbono, aço níquel cromo | 206 | 79,4 | 0,3 | Vidro | 55 | 1,96 | 0,25 |
| Liga de aço | Vidro orgânico | 2,35-29,42 | |||||
| Aço fundido | 202 | 0,3 | Borracha | 0,0078 | 0,47 | ||
| Cobre puro laminado | 108 | 39,2 | 0,31-0,34 | Baquelite | 1,96-2,94 | 0,69-2,06 | 0,35-0,38 |
| Cobre puro estirado a frio | 127 | 48,0 | Plástico fenólico sanduíche | 3,92-8,83 | |||
| Bronze de estanho fosforoso laminado | 113 | 41.2 | 0,32-0,35 | Celulóide | 1,71-1,89 | 0,69-0,98 | 0,4 |
| Latão estirado a frio | 89-97 | 34,3-36,3 | 0,32-0,42 | Náilon 1010 | 1.07 | ||
| Bronze manganês laminado | 108 | 39,2 | 0,35 | Cloreto de polivinila não plastificado | 3,14-3,92 | 0,35-0,38 | |
| Alumínio laminado | 68 | 25,5-26,5 | 0,32-0,36 | teflon | 1,14-1,42 | ||
| Fio de alumínio trefilado | 69 | Polietileno de baixa pressão | 0,54-0,75 | ||||
| Bronze de alumínio fundido | 103 | 41.1 | 0,3 | Polietileno de alta pressão | 0,147-0,245 | ||
| Bronze de estanho fundido | 103 | 0,3 | concreto | 13,73~39,2 | |||
| Liga de duralumínio | 70 | 26,5 | 0,3 | 4,9-15,69 | 0,1-0,18 |
Afinal, quando as tensões internas não podem ser medidas diretamente, a tensão pode ser calculada medindo a deformação e multiplicando-a pelo módulo de ela do material.